这道题标准解法应该是diljstra，但是数据太水导致floyd算法也能过，所以就用floyd了(好写)
floyd理解难度和代码量比diljstra和spfa要低，建议先理解透floyd再去学习另外两种最短路算法
这类题统称最短路问题，其核心思想就是
对于A,B点，能否找到C点使A到C的距离加上C到B的距离要小于A直接到B的距离
举个例子，假如有4个点 1 2 3 4，他们之间的关系是
1点与2点有一条距离为3的路
2点与4点有一条距离为7的路
1点与3点有一条距离为5的路
3点与4点有一条距离为1的路
求点1到点4的最短路
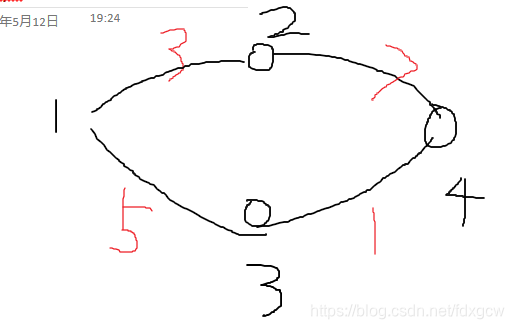
根据题可以画出图
红色的数为路的距离

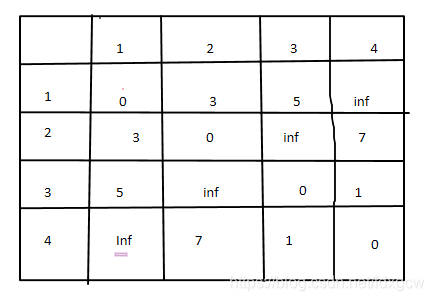
同时，我们也可以写出邻接矩阵(inf指两个点之间没有路)

根据上面的算法，我们来对A B C三个点进行枚举

for(int k=1;k<=4;k++){//枚举C点
	for(int i=1;i<=4;i++){//枚举A点
		for(int j=1;j<=4;j++){//枚举B点
			if(i==j||i==k||j==k)continue;
		}
	}
}

首先C点为1 A点为1 B点为1 计算1点到1点的距离是否大于1点到1点加上1点到1点的距离，这显然是没有意义的，所以直接跳过
接下来是C为1 A为1 B为2，计算1点到2点的距离是否大于1点到1点加上1点到2点的距离，这同样是没有意义的，跳过
跳过一些无意义的部分，我们直接来到第一个有意义的点
C为1 A为2 B为3，计算2点到3点的距离是否大于2点到1点加上1点到3点的距离
从邻接表或图可知，2到1的距离是3，1到3的距离是5,而2到3的距离为inf，即无限远，所以2到3是可以以1点为中转站到达，当前的最短距离是5+3=8，所以此时我们就可以更改邻接表上的数据
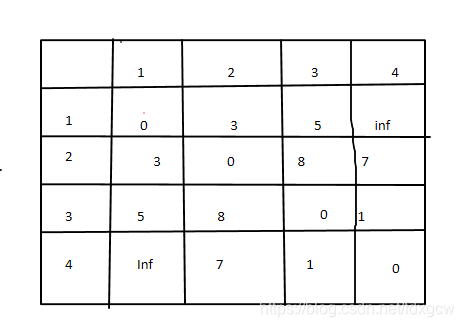
arr[2][3]=8;arr[3][2]=8
此时邻接表数据为
接下来是C=1,A=2,B=4;2到4为7，2到1为3，1到4为inf，所以这次不会产生变化
以此类推，就能计算出各个点之间两两之间的最短距离
代码如下
注：在最短路计算中常用0x3f3f3f3f来指代最大值或无限远，常用memset(a,0x3f,sizeof a)来对整个初始数组赋上无限远的初值

#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <queue>
using namespace std;
const int N = 1005;
int n, m, s, t, tot;
int map[N][N];

int main() {
	scanf("%d%d%d%d", &n, &m, &s, &t);
	memset(map, 0x3f, sizeof map);
	for (int i = 0; i <= n; i++) {
		map[i][i] = 0;
	}
	for (int i = 0; i < m; i++) {
		int u, v, w;
		scanf("%d%d%d", &u, &v, &w);
		map[u][v] = min(map[u][v], w); //两个点可能存在多条道路，去最小
		map[v][u] = min(map[v][u], w);
	}
	for (int k = 1; k <= n; k++) {//枚举所有的C点
		for (int i = 1; i <= n; i++) {//枚举所有A点
			for (int j = 1; j <= n; j++) {//枚举所有B点
				if (map[i][j] > map[i][k] + map[k][j]) {
					map[i][j] = map[i][k] + map[k][j];
				}
			}
		}
	}
	if (map[s][t] == 0x3f3f3f3f) {
		printf("-1\n");
	} else {
		printf("%d\n", map[s][t]);
	}
}