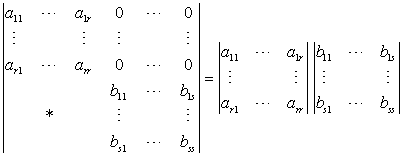
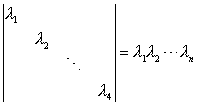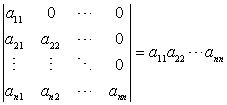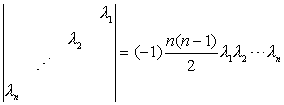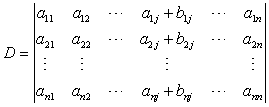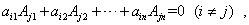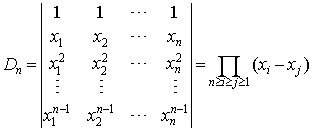1-行列式的基本公式

• 公式1
  
  
• 公式2
  
• 公式3
  

2-行列式的基本性质

• 性质1　行列式与它的转置行列式相等。
• 性质2　互换行列式的两行(列)，行列式变号。
  
  • 推论　如果行列式有两行(列)完全相同，则此行列式为零。X=-X–>X=0
• 性质3　行列式的某一行(列)中所有的元素都乘以同一数k，等于用数k乘此行列式。
  
  • 推论　行列式中某一行(列)的所有元素的公因子可以提到行列式符号的外面。
• 性质4　行列式中如果有两行(列)元素成比例，则此行列式等于零。
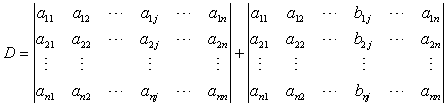
• 性质5：若行列式的某一行(列)的元素都是两数之和，例如第j列的元素都是两数之和：
  
  
• 性质6　把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去，行列式不变。

3-行列式的求值

余子式和代数余子式

（1）行公因子可提取到外部，但不能删除；
（2）行列式可进行行列级加减，不改变行列式值
（3）定理3.1 行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和。

• 推论 行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零
  

• 范德蒙德(Vandermonde)行列式
  

4-克拉默法则求解方程组

• 数学概念
  

• 定理4.1 如果线性方程组(1)的系数行列式D≠0，则(1)一定有解，且解是唯一的。

• 定理4.1’ 如果线性方程组(1)无解或有两个不同的解，则它的系数行列式必为零。

• 定理4.2 如果齐次线性方程组(2)的系数行列式D≠0，则齐次线性方程组(2)没有非零解。

• 定理4.2’ 如果齐次线性方程组(2)有非零解，则它的系数行列式必为零。

5-典型例题