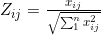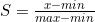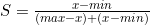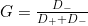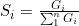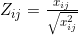| 时间 | 2020年5月4日 | 组别 | 数学建模 | 姓名 | Zkaisen |
|
本
周
完
成
工
作
总
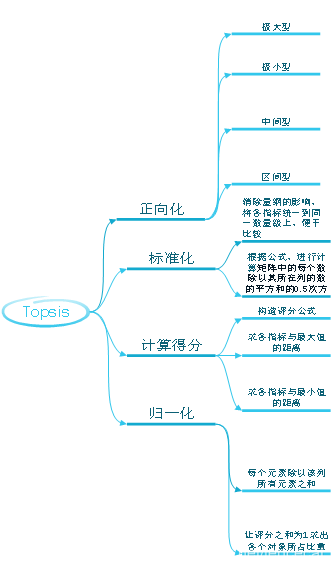
结 | 这一周我主要学习了TOPSIS法即优劣解距离向量法。 1.AHP的局限性 前两周主要学习了层次分析法,层次分析法存在这样一些局限性: (1)层次分析法主观性很强,我们建模过程中判断矩阵都是自己手动填写的。 (2)层次分析法方案层不能太多,太多的话,构建的判断矩阵很可能不能通过一致性检验。而且随机一致性指标RI表中n也只给到了15。 (3)层次分析法是根据成对比较法和1~9尺度表构建判断矩阵得到数据的,对于一些有已知数据题目,层次分析法是不能很好利用原始数据的。 2.TOPSIS优点 针对AHP的上述局限性,学习TOPSIS可以弥补层次分析法的一些缺点: (1)优劣解距离法可以充分利用原始数据信息,且其结果能充分反应各评价方案与最优方案的接近程度。 (2)对样本容量没有严格限制,数据计算简单易行,无需数据检验。(topsis法适用于两个以上) 3.Topsis法简介 1981年,C.L.Hwang和K.Yoon首次提出了Topsis,全称Technique for Order Preference by Similarity to an Ideal Solution,可翻译为逼近理想解排序法,国内常称为优劣解距离法。它是一种常用的综合评价方法。 4.Topsis的基本过程 (1)原始矩阵正向化,得到正向化矩阵 a.指标类型 指标类型一般分为四种,极大型指标、极小型指标、中间型指标、 区间型指标。 极大型指标越大越好,极小型指标越小越好,中间型指标越接近中 间值越好,区间型指标落在区间内最好。 b.正向化的公式 正向化就是将原始数据指标都转化为极大型指标。 极小型——极大型: 当指标值中没有“0”时也可用公式: 中间型——极大型: 区间型——极大型:
注:M为距离区间最远的距离,即 当x小于区间下限a时, 当x大于区间上限b时, (2)对正向化矩阵标准化 标准化公式: (3)计算得分并归一化 a.构造评分公式: 评分公式变形: Topsis的思想:最优解即最大值,最劣解即最小值。 b.计算D+与D-: 定义最大值:Z+向量用于存放标准化矩阵中每一列的最大值 定义最小值:Z-向量用于存放标准化矩阵中每一列的最小值 定义第i个(i=1,2,...,n)个评价对象与最大值的距离:等于第i行每一个元素与其所在列的最大值的差的平方和的0.5次方 定义第i个(i=1,2,...,n)个评价对象与最大值的距离:等于第i行每一个元素与其所在列的最小值的差的平方和的0.5次方 c.计算未归一化的得分记为G
d.对得分进行归一化
5.问题思考 (1)为什么要进行正向化? (2)为什么要进行标准化,标准化是为了消除量纲的影响,那么可不可以用下面的公式来实现? (2)构造评分公式的含义,背后的思想 6.代码思路及实现 (1)通过软件Matlab实现 a.先根据每一步的公式理清思路 b.根据分析,使用for循环实现较为可行 (学习编程软件中for循环相关操作) c.根据步骤分块实现不同的功能 d.代码编写过程中尽量使每一步结果都输出,这样当结果与预期 不符时方便纠错。并且可输入简单的数值对代码进行检验,查找错 误所在之处,进而修改完善。 e .找相关数据进行结果检验,验证结果的准确性。 (2)通过软件SPSS实现 a.论文中有可通过SPSS实现标准化,导入数据,进行相应操作后,标准化结果却与MATLAB中的结果不同。学习SPSS标准化,有两种不同的标准化方式,即z-score标准化和离差标准化。 b.默认的是z-score标准化。其公式不同于我们步骤中的公式。它是基于原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。将A的原始值x使用z-score标准化到x’。 步骤如下: 首先求出各变量(指标)的算术平均值(数学期望)xi和标准差si ;进行标准化处理:zij=(xij-xi)/si,其中zij为标准化后的值;xij为实际值。 最后将逆指标前的正负号对调。 z-score标准化后的变量值围绕0上下波动,大于0说明高于平均水平,小于0说明低于平均水平。 c.我们MATLAB中使用的公式是SPSS中标准化的规范化方法,也叫离差标准化,是对原始数据的线性变换,使结果映射到[0,1]区间。 可以通过SPSS的语法编辑窗口来编写代码实现TOPSIS(需要学习并掌握SPSS的基础语法才能实现代码的功能实现) (3)MATLAB代码简单思路
| ||||
|
遇 到 的 问 题 | 所遇到的问题: 1.没有理解在论文6.2.2中先用算术平均数计算对应的平均值? 后来懂了,他是通过VISSIM软件汇总数据,取平均值的. 2.表4中处理后的数据是同趋化后的数据吧,可是我通过代码求出的数据却和论文中的不同,本以为是标准化方法不同的原因,可是我用SPSS进行标准化后的数据进行得分计算,结果仍然不一样。 3.虽然通过论文学习了Matlab相关知识,但实现不了学习的论文中的内容. 论文中的数据都是自己通过统计得到的。 总结: 1.不懂的地方多思考,多百度 2.遇到问题,多尝试,用不同的方法来测试验证结果 3.学习优秀论文要注重学其方法,不必拘泥于一些具体实现上 (因为具体的功能实现可能需要具体的环境) | ||||
|
备
注
| Matlab代码 % TOPSIS法 % % 导入数据 % clear;clc;close all;%清屏,clc清空命令窗口,clear清空工作区,clos all清除图形 % 点击工作区右键,新建并为矩阵命名为X % 把数据复制到工作区 % 在excel中复制数据,在回到Excel中右键,点击粘贴excel中的数据(ctrl+shift+V) % 关掉这个窗口,右键另存,保存为mat文件 % (下次就不用复制粘贴了,只需要使用load命令即可加载数据) % load data_kaifangqian.mat [r,c]=size(X) Max_total=max(X)%每一列数据的最大值,它是一个行向量 Min_total=min(X)%每一列数据的最小值,它是一个列向量 B=zeros(1,c);%定义一个0矩阵用来存放指标类型 disp('请输入指标类型,0表示极大型,1表示极小型,2表示中间型,3表示区间型') for j=1:c %通过for循环依次从键盘输入指标类型对应的数字
B(j)=input('please enter a type:'); end disp(B)
%% %%指标正向化 C=zeros(1,c) A=zeros(r,c)%这里我用A矩阵存放正向化后的数据 for j=1:c if B(j)==0%无需正向化 for i=1:r A(i,j)=X(i,j);%直接将原数值赋值给矩阵A end elseif B(j)==1%该列数据为极小型,需要正向化 for i=1:r A(i,j)=Max_total(j)-X(i,j); end elseif B(j)==2%中间型指标,需要正向化 mid=input('中间值mid:')%中间值也就是公式中的x(best) for i=1:r C(i)=abs(X(i,j)-mid);%abs函数是绝对值函数 end Max_mid=max(C);%用Max_mid来存放离中间值最远的值,也就是公式中的M for i=1:r A(i,j)=1-C(i)./Max_mid;%代入公式计算正向化后的指标数值,并赋值给矩阵A end
elseif B(j)==3%指标类型是区间型指标的情况
a=input('请输入区间下限:')%区间下限,公式中的a b=input('请输入区间上限:')%区间上限,公式中的b e=(a-Min_total(j));%求出离区间下限最远的距离并赋值给e d=(Max_total(j)-b);%求出离区间上限最远的距离并赋值给d M=max(e,d);%比较e和d的值,并把最大值赋值给M for i=1:r if (X(i,j)>=a)&&(X(i,j)<=b) %如果指标刚好在区间内,那么正向化后的值为1 A(i,j)=1;
elseif X(i,j)<a %如果Xi小于a,用公式计算正向化后的数值并赋值给矩阵A A(i,j)=1-(a-X(i,j))./M;
elseif X(i,j)>b%如果xi大于b,用公式计算正向化后的数值并赋值给矩阵A A(i,j)=1-(X(i,j)-b)./M ; end end end end %%
%标准化 %方法一结合上节课层次分析法,通过repmat函数,sum函数和乘方运算来实现 Z=A./repmat(sum(A.*A).^0.5,r,1); disp(Z); %方法二通过for循环来实现 for i=1:r for j=1:c D=sum(A.*A).^0.5 ;% A.*A就是矩阵A的每一个元素平方,sum求和得到的是一个行向量,存放矩阵中每一列元素的和 Z=A./repmat(D,r,1); %repmat函数表示将A复制m*n块,及把A作为的元素,Z由m*n个A平铺而成。 end end disp(Z)
%% % % 求得分并进行归一化 S=zeros(r,1);%存放最终的归一化后的得分 G=zeros(r,1);%存放未归一化的得分 DP=zeros(r,1);%存放D+ DN=zeros(r,1);%存放D- E=zeros(r,c); F=zeros(r,c); Max_Z=max(Z);%存放标准化后每一列的最大值 Min_Z=min(Z);%存放标准化后每一列的最小值 for i=1:r for j=1:c E(i,j)=(Max_Z(j)-Z(i,j)).*(Max_Z(j)-Z(i,j));%就是求解D+公式中分母中根号下面的内容 F(i,j)=(Min_Z(j)-Z(i,j)).*(Min_Z(j)-Z(i,j));%就是求解D-公式中分母中根号下面的内容 end DP(i)=sum(E(i,:)).^0.5;%第i个(i=1,2,...,n)个评价对象与最大值的距离。这里用到了E(i,:),就是取第i行的所有数据 DN(i)=sum(F(i,:)).^0.5;%第i个(i=1,2,...,n)个评价对象与最小值的距离
G(i)=DN(i)/(DP(i)+DN(i)); end disp(DN) disp(DP) disp(G)
%%对得分进行归一化
for i=1:r S(i)=G(i)/sum(sum(G)); end disp(S) %% | ||||
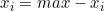
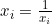
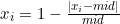 (其中mid为中间值)
(其中mid为中间值)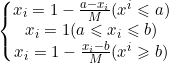
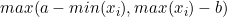 当x在区间内时,正向化后的值为1;
当x在区间内时,正向化后的值为1;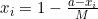 ;
;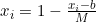 ;
;