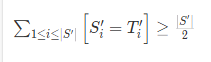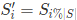比赛链接

A 生不逢七

题目描述(题目链接添加链接描述)：

睡前游戏中最简单又最好玩的游戏就是这个啦！

该游戏规则为：多名玩家轮流报数，当要报的数字中含有 7 或者是 7 的倍数时（例如 37，49），不能将该数报出来，要换一种提前规定好的方式报数，当一个人报错或者报慢了这个人就输了。

我们认为玩家是围成一圈进行游戏的，第 n 个人报完数之后，会轮到第 1 个人报数。

现在告诉你玩家的总人数以及你上一个人报的数（用数字表示，即便这个数含有 7 或者是 7 的倍数），你需要预测接下来 k轮你要报的数字，当你需要报的数字含有 7 或者是 7 的倍数时，你需要输出字符 p。

输入描述：
第一行一个整数 T，表示输入数据的组数。

接下来每组数据中均只有一行数据，每行三个整数 n，a，k，分别表示玩家数量，你的上一位玩家报的数，你需要模拟的游戏轮数。

数据保证 1≤T,n,k,a≤100。

输出描述：
共 T 行，每行输出 k 个整数或者字符 p

示例：
输入：

3
2 16 3
3 69 3
2 1 10

输出：

p 19 p
p p p
2 4 6 8 10 12 p 16 18 20

解题思路：

简单的签到题，

• 每次报的数是前一个数加1，最终的输出是是输出每轮自己报的数，下一次自己报的数也就是在上一次自己报的数上加上玩家数，
• 这道题也就可以理解为每一组数据，有k次循环，因为a是上一个人报的数，所以在第一轮也就是第一次循环，输出a+1,后面输出的数持续加n

解题代码：

C++：

#include<bits/stdc++.h>
using namespace std;
int fun(int a)//判断该数能不能报
{
    if(a%7==0)
        return 0;
    while(a)
    {
        if(a%10==7)
            return 0;
        a/=10;
    }
    return 1;
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n,a,k;
        cin>>n>>a>>k;
            a++;   
        for(int i=0;i<k;i++)
        {
            if(fun(a))
            cout<<a<<" ";
            else
                cout<<'p'<<" ";
            a+=n;
        }
        cout<<endl;
    }
    return 0;
}

C:

#include<stdio.h>
int fun(int a)
{
    if(a%7==0)
        return 0;
    while(a)
    {
        if(a%10==7)
            return 0;
        a/=10;
    }
    return 1;
}
int main()
{
    int t=0;
    scanf("%d",&t);
    while(t--)
    {
        int n,a,k;
        scanf("%d%d%d",&n,&a,&k);
        a++;
        while(k--)
        {
            if(fun(a))
            printf("%d ",a);
            else
            printf("p ");
            a=a+n;
        }
        printf("\n");
    }
    return 0;
}

B 交换数字

题目描述(题目链接)：

Baijiaohu有两个长度均为 n 且不包含前导零的数字 a,b ，现在他可以对这两个数字进行任意次操作：
选择一个整数1≤i≤n ,并交换 a,b 的第 i 位 。
请输出任意次操作后 a×b 的最小值，由于答案可能很大，请对 998244353 取模

输入描述：

第一行输入一个数字 n 代表两个数字的长度
第二到三行输入两个字符串 a,b
1≤n≤2×10⁵

输出描述：
输出一个 ans 表示最后的答案
请对 998244353 取模

示例1：
输入

3
159
586

输出

91884

示例2：
输入：

10
1578959751
1786548221

输出：

410002876

解题思路：

• 一开始我就觉得，要求a*b最小，那就把a和b其中一个数交换到每一位都是最小，这有些带猜，也是被我猜对了
• 正确的思路是想到4ab=(a+b)²-(a-b)²,只要a-b最大时，a*b就是最小了，也就是a最大，b最小时，

解题代码：

C++:

#include<bits/stdc++.h>
using namespace std;
#define mod 998244353
int main()
{
    int n;
    cin>>n;
    char a[n],b[n];//用字符串收取方便后面交换这两个数的每一位
    cin>>a>>b;
    for(int i=0;i<n;i++)
    {
        char c;
        if(a[i]>b[i])
        {
            c=a[i];
            a[i]=b[i];
            b[i]=c;
        }
    }
    long long a2=0,b2=0;
    for(int i=0;i<n;i++)
    {
        a2=(a2*10+a[i]-'0')%mod;
        b2=(b2*10+b[i]-'0')%mod;
    }
    cout<<a2*b2%mod;
    return 0;
}

C:

#include<stdio.h>
#define ll long long
#define mod 998244353
int main()
{
    int n;
    scanf("%d",&n);
    char a[n],b[n];
    scanf("%s%s",a,b);
    for(int i=0;i<n;i++)
    {
            if(a[i]>b[i])
            {
                char t=a[i];
                a[i]=b[i];
                b[i]=t;
            }
    }
        ll A=0,B=0;
        for(int i=0;i<n;i++)//把字符串再转成数字
        {
            A=(A*10+(a[i]-'0'))%mod;
            B=(B*10+(b[i]-'0'))%mod;
        }
        printf("%lld",A*B%mod);
    return 0;
}

C 老虎机

题目描述(题目链接)：

老虎机游玩规则：共有三个窗口，每个窗口在每轮游玩过程中会等概率从图案库里选择一个图案，根据最后三个窗口中图案的情况获得相应的奖励。

你有一个老虎机，你可以设定这个老虎机图案的数量和收益规则。

现在你设定了图案的数量为 𝑚，没有相同的图案得𝑎 元，一对相同的图案 𝑏 元，三相同的图案 𝑐 元。

你想知道在你设定的规则下，单次游玩期望收益是多少？答案对 998244353取模。

根据 逆元 的定义，如果你最后得到的答案是形如^a/_b的分数，之后你需要对𝑝 取模的话，你需要输出(a*b^mod-2) mod p来保证你的答案是正确的。

输入描述：
第一行一个整数 𝑇(1≤𝑇≤10⁴)。
接下来 T 行，每行四个整数 𝑚,𝑎,𝑏,𝑐(1≤𝑚,𝑎,𝑏,𝑐≤10⁶)。

输出描述:
一个整数表示答案，答案对 998244353 取模。

输入示例：

1
2 2 3 4

输出示例：

748683268

说明：
1/4 的概率出现三个相同的图案，收益为 4，3/4 的概率出现两个相同的图案，收益为 3，不可能出现没有相同图案的情况，期望收益为 13/4。

解题思路：

• 一道数学题，因为逆元，要用到快速幂的方法，快速幂就是把a^b分解为多个a²,
• 题目说了等概率从图案库选择一个图案，每个窗口选择图案的概率是1/m,总事件数也就是m³
• 没有相同的事件数是m(m-1)(m-2),除以总事件数m³,也就是概率：(m-1)(m-2)/m²,期望也就是概率再乘以a
• 全相同的事件数是m,概率是1/m²,
• 一对相同的图案的概率就是1-没有相同的概率-全相同的，化简后为，3(m-1)/m²
• 注意代码中求最后的期望时的A，B，C,都要每乘一个数都要取一次模，不然可能会过大，导致出错
• 可知，化简后三个事件概率的分母都是一样的，所以只需要调用一次快速幂

解题代码：

C++:

#include<bits/stdc++.h>
using namespace std;
const long long mod=998244353;
long long fun(long long a)//快速幂
{
    long long res=1;
    long long x=mod-2;
    a%=mod;
    while(x>0)
    {
        if(x%2==1)//幂为奇数时
            res=(res*a)%mod;
        a=(a*a)%mod;
        x/=2;
    }
    return res;
}
int main()
{
    long long t;
    cin>>t;
    while(t--)
    {
    long long m,a,b,c;
    cin>>m>>a>>b>>c;
    long long mm=m*m%mod;
    mm=fun(mm);
    mm%=mod;
    long long C=mm*c%mod;//全相同的期望
    long long A=mm*(m-2)%mod*a%mod*(m-1)%mod;//全不同的期望
    long long B=mm%mod*3*b%mod*(m-1)%mod;//一对相同的期望
    cout<<(A+B+C)%mod<<endl;        
    }

    return 0;
}

C:

#include<stdio.h>
#define ll long long
#define mod 998244353
ll fun(ll mm)
{
    ll m=1;
    ll x=mod-2;
    while(x>0)
    {
        if(x%2==1)
            m=m*mm%mod;
        mm=mm*mm%mod;
        x/=2;
    }
    return m;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        ll m,a,b,c;
        scanf("%lld%lld%lld%lld",&m,&a,&b,&c);
        ll mm=m*m%mod;
        mm=fun(mm);
        mm%=mod;
        ll A=mm*a%mod*(m-1)%mod*(m-2)%mod;
        ll B=mm*b%mod*3%mod*(m-1)%mod;
        ll C=mm*c%mod;
        printf("%lld\n",(A+B+C)%mod);
    }
    return 0;
}

D:幻兽帕鲁

题目描述(题目链接)

在幻兽帕鲁中，不同的帕鲁能干不同的工作，现在我们要对帕鲁进行分类以便他们能够更好的进行压榨。

你有 2ⁿ 只帕鲁，初始给每只帕鲁一个工号，并让帕鲁按 [0,2ⁿ-1] 工号的顺序排成一队。

当我们对区间 [l,r] 的帕鲁进行操作时，我们会对该区间的帕鲁按顺序进行临时编号 [0,r−l] ，记mid=(l+r)/2,我们将临时编号为偶数和奇数的帕鲁，分别按顺序置于区间 [l,mid] 和 [mid+1,r] ，并递归对这两个区间进行上述操作，直到区间长度为 1

现在我们对 [0,2ⁿ-1]的幻兽进行一次操作，然后给你m次询问，每次询问x位置的帕鲁工号是多少？

输入描述:
第一行两个整数n,m(0<n=<60,0<m<=10⁵)
接下来 m 行，每行一个整数 x 表示询问第 x 个位置的帕鲁的工号，位置从 0 开始计数。

输出描述：
输出每次询问的帕鲁的工号。

示例1：
输入：

2 4
0
1
2
3

输出：

0
2
1
3

示例2：
输入：

3 4
0
2
5
7

输出：

0
2
5
7

解题思路：

这题当时题目都没看明白，这题可以通过找规律来解，

• 这里图里举了个例子，n=4时的数据，可以看到结果的工号是原来的二进制的逆序
• 还有另一种思路，是最后编号为x的位置下的工号,就是开始工号为x的最后的编号，
• 要找最后编号为x的位置下的工号，思路就是用二分法，递归，设两个变量p,t
• p：当前操作的区间在整个区间 [0, 2ⁿ-1] 中的位置，初始为 1
• t：当前操作的区间的起始工号，初始为 0,由图所示，最后的工号会划分为一个偶数工号区间，一个奇数工号区间，这两个区间会在第一次操作就划开了

解题代码：

C++：
利用结果是二进制逆序的思路：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
    int n,m;
    cin>>n>>m;
    while(m--)
    {
        ll x;
        cin>>x;
        char s[n];
        memset(s,'0',sizeof(s));//初始化字符串
        int i=0;
        while(x)//将x转换为二进制字符串
        {
            s[i]=x%2+'0';
            x>>=1;
            i++;
        }
        ll y=0;//将二进制字符串转为十进制，
        for(int j=0;j<n;j++)
        {
            y=y*2+s[j]-'0';
        }
        cout<<y<<'\n';
    }
 return 0;
}

用二分法，递归：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll x;
ll qpow(ll a,ll n)//快速幂函数
{
    ll res=1;
    while(n)
    {
        if(n%2)
        res=res*a;
        a*=a;
        n>>=1;
    }
    return res;
}
ll work(ll l,ll r,ll p,ll t)
{
    if(l==r)
    return t;
    ll mid=(l+r)>>1;
    if(mid>=x) return work(l,mid,p<<1,t);//可以看到p是区间元素差值
    else
    return work(mid+1,r,p<<1,t+p);
}
int main()
{
    ll n,m;
    cin>>n>>m;
    while(m--)
    {
        cin>>x;
        ll l=0;
        ll r=qpow(2,n)-1;
        ll t=work(l,r,1,0);
        cout<<t<<'\n';
    }
    return 0;
}

C:

#include<stdio.h>
#include<string.h>
#define ll long long
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    while(m--)
    {
        ll x;
        scanf("%lld",&x);
        char s[n];
        memset(s,'0',sizeof(s));
        int i=0;
        while(x)
        {
            s[i]=x%2+'0';
            i++;
            x/=2;
        }
        ll y=0;
        for(i=0;i<n;i++)
        {
            y=y*2+s[i]-'0';
        }
        printf("%lld\n",y);
    }
    return 0;
}

E：奏绝

题目描述(题目链接)：

你拥有一个黑之章和白之章构成的序列，你可以用它进行演奏。

对于一次演奏的区间，如果这个区间的两个端点一个为黑之章，一个为白之章，那么该次演奏将会产生该区间长度的影响值，否则该次演奏影响值为0.

区间长度定义为左端点到右端点的距离，比如i到i+1的距离为1

对于 𝑚次询问，你要求出对于每次询问的区间，你在其所有子区间演奏的影响值的和，结果对998244353取模

输入描述：
第一行一个整数 𝑛,𝑚(1≤n,m≤2×10⁵ )。

接下来一行 01 序列 c_i (c_i∈{0,1}) 表示黑之章白之章的排列顺序，其中 1 表示黑之章，0 表示白之章。

接下来 𝑚 行，每行两个整数 l,r (1≤l≤r≤n)，表示一次询问的区间。

输出描述：
m 行，每行一个整数，表示对于每次询问的答案对 998244353 取模。

示例1：

输入：
5 4
01001
1 3
2 5
3 4
1 5

输出：
2
6
0
11

解题思路：

这题也算是找规律，不能暴力，暴力拿不了满分，会超时

• 找区间前缀和的规律，就题目给的示例01001来讨论，开一个数组sum来存储每个点到左端点区间的影响值，
• 当当前点为1时，sum[5]=sum[5-1]+(5-1)+(5-3)+(5-4),分析下，sum[5]=sum[5-1]+(5+5+5)-(1+3+4),可以看出与前面0的个数有关，还有0所在位置，再开两个数组统计前面0的个数c0，前面0的位置和s0,可得出sum[i]=sum[i-1]+i*c0[i]-s0[i],
• 当当前点为0时，又不一样，不过还是同样的想法，与前面1的个数有关，还有1所在位置，再开两数组c1,s1,得出sum[i]=sum[i-1]+c1[i]*i-s1[i]
• 题目要求求出某一区间的影响值ans,首先想到的是ans=sum[r]-sum[l-1],
• 但这还不够，因为还有区间内的1与区间外的0的影响值未去掉，还有区间内的0与区间外的1的影响值，
• 先推区间内的1与区间外的0，区间内1的数量：c1[r]-c1[l-1],区间内1的位置和：s1[r]-s1[l-1],区间外0的个数：c0[l-1],区间0的位置和：s0[l-1],得出(s1[r]-s1[l-1])*c0[l-1]-(c1[r]-c1[l-1])*s0[l-1]
• 区间内的0与区间外的1的影响值，区间内0的数量：c0[r]-c0[l-1],区间内0的位置和：s0[r]-s0[l-1],区间外1的个数：c1[l-1],区间外1的位置和：s1[l-1],得出(s0[r]-s0[l-1])*c1[l-1]-(c0[r]-c0[l-1])*s1[l-1]

解题代码：

如果是题目没读懂，可以看看我暴力的代码：

#include<bits/stdc++.h>
using namespace std;
# define mod 998244353
int main()
{
    int n,m;
    cin>>n>>m;

    string s;
    cin>>s;
    while(m--)
    {
        int l,r,count=0;//count总计影响值，硬遍历累加
        int a[n],index=0;
        memset(a,-1,sizeof(int));        
        cin>>l>>r;
        l--;
        r--;
        for(int i=l;i<=r;i++)
        {
            if(s[i]=='1')
            {
                a[index++]=i;
            }
        }
        if(index==0)
        cout<<0<<'\n';
        else
        {
            for(int i=0;i<index;i++)
            {
                for(int j=l;j<a[i];j++)
                {
                    if(s[j]=='0')
                    {
                        count+=a[i]-j;
                    }
                }
                for(int j=r;j>a[i];j--)
                {
                    if(s[j]=='0')
                    count+=j-a[i];
                }
            }
            cout<<count<<'\n';
        }
        
    }
  return 0;
}

满分的：
C++：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define mod 998244353
const ll N=4e5;
ll c0[N],c1[N],s0[N],s1[N],sum[N];
int main()
{
    int n,m;
    cin>>n>>m;
    char s[N]={'0'};
    cin>>s+1;
    for(int i=1;i<=n;i++)
    {
        c0[i]=c0[i-1]+(s[i]=='0');//统计0的个数
        c1[i]=c1[i-1]+(s[i]=='1');//统计1的个数
        s0[i]=s0[i-1]+i*(s[i]=='0');//统计0的位置和
        s1[i]=s1[i-1]+i*(s[i]=='1');//统计1的位置和
        if(s[i]=='1')
        sum[i]=sum[i-1]+c0[i]*i-s0[i];//影响值
        else
        {
         sum[i]=sum[i-1]+c1[i]*i-s1[i];            
        }
        s0[i]%=mod;
        s1[i]%=mod;
         sum[i]%=mod;
    }
    while(m--)
    {
        ll l,r,ans=0;
        cin>>l>>r;
        ans=sum[r]-sum[l-1]-(c0[l-1]*(s1[r]-s1[l-1])-s0[l-1]*(c1[r]-c1[l-1]));
        ans=ans-(c1[l-1]*(s0[r]-s0[l-1])-s1[l-1]*(c0[r]-c0[l-1]));
        ans=(ans%mod+mod)%mod;//有没有大佬说下这里为什么不能直接ans%=mod,在网上搜只搜到了ans=(ans%mod+mod)%mod可以处理负数的情况，可是按照我这思路感觉不到会有负数的情况
        cout<<ans<<'\n';
    }
    return 0;
}

C:

#include<stdio.h>
# define mod 998244353
#define N 400000
typedef long long ll;
ll c0[N],c1[N],s0[N],s1[N],sum[N];
char s[N];
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    scanf("%s",s+1);
    for(int i=1;s[i];i++)
    {
        c0[i]=c0[i-1]+(s[i]=='0');
        c1[i]=c1[i-1]+(s[i]=='1');
        s0[i]=s0[i-1]+i*(s[i]=='0');
        s1[i]=s1[i-1]+i*(s[i]=='1');
        if(s[i]=='1')
        {
            sum[i]=sum[i-1]+i*c0[i]-s0[i];
        }
        else
        {
            sum[i]=sum[i-1]+i*c1[i]-s1[i];
        }
        s0[i]%=mod;
        s1[i]%=mod;
        sum[i]%=mod;
    }
    while(m--)
    {
        ll l,r,ans=0;
        scanf("%lld%lld",&l,&r);
        ans=sum[r]-sum[l-1];
        ans=ans-((s1[r]-s1[l-1])*c0[l-1]-(c1[r]-c1[l-1])*s0[l-1]);
        ans=ans-((s0[r]-s0[l-1])*c1[l-1]-(c0[r]-c0[l-1])*s1[l-1]);
        ans=(ans%mod+mod)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

F:本初字符串

题目描述(题目链接):

定义一个字符串S的本初为T,当且仅当 S 和 T 自我复制足够多的次数，使其长度相等后，对应位置相同的字符的位置，不小于复制之后的字符串的长度的一半，给定S，求满足条件的 最短 的 T，若仍有多个相同长度的 T 满足条件，请输出其中 字典序最小 的 T。

形式化地讲，记一个字符串 S 的长度为 ∣S∣，S 和 T 分别自我复制若干次产生的新字符串为 S′ 和 T′ ，我们若称一个字符串 S 的本初为 T，需要满足
|S’| = |T’|

请注意公式中并没有取整符号。
式子中出现的中括号为艾弗森括号，如果内部的表达式为真则值为1，反之值为0，[1=1] 的值为 1，而 [1=0] 的值为 0。

一个新字符串 S′是字符串S 自我复制得来，可以认为对于任意i∈[0,∣S′∣)，都有​

输入描述：
一行一个整数 T 表示数据组数，接下来每组数据一行一个字符串 S (∑∣S∣≤2×10⁵)，保证输入均为小写字母。

输出描述：
T 组数据，对于每组数据，一行一个字符串，表示 S 的本初。

示例1

输入：

2
ab
abc

输出：

a
aac

解题思路：

思路大伙去看看别人的吧(￣ ‘i ￣;)

我只说下代码的逻辑：
找出字符串s的s.size()的因子，本初字符串t的长度就是其中一个因子，t模拟s的子串进行比对，按照题意

解题代码：

C++:

#include <iostream>
#include <string>
#include <vector>
using namespace std;

string find(const string& s, int len) {
    vector<vector<int>> count(len, vector<int>(26));//count用于统计每个位置上各个字符出现的次数
    vector<int> vis(len + 1);
    int n = s.length();//字符串s的长度

    for (int i = 0; i < n; i++) {
        count[i % len][s[i] - 'a']++;//将字符串 s 中的字符按照其在 T 中的位置进行分组统计
    }
/*
 对于上面这一段for可能不好理解，举个例子比如abc和abcabcabc,按照题意要将abc复制到跟abaabcabc一样长再比对，
 在这个复制的过程中abc中的a会对应着abcabcabc中位置1，4，7，剩下两个字符也是这样，
*/
    for (int i = len - 1; i >= 0; i--) {//从T的最后一位往前构建子串来比对
        for (int j = 0; j < 26; j++) {//这里就是从字符串 s 中的字符按照其在 T 中的位置进行分组统计中找出每一组最多的那个字符
            vis[i] = max(vis[i], vis[i + 1] + count[i][j]);
        }
    }

    if (vis[0] * 2 < n) {//vis[0]也就是完整的t与s的相同字符数，如果乘以2仍小于s的长度，也就不符题意了
        return "";
    }

    string ans(len, ' ');//初始化ans
    int pre = 0;//用于记录前面已经构建的字符
    for (int i = 0; i < len; i++) {
        for (int j = 0; j < 26; j++) {
            if ((pre + count[i][j] + vis[i + 1]) * 2 >= n) {//确定是否选择当前字符 j 放在位置 i，
                /*
                这个if也有点绕，这里就是确保本初字符串T的字典序最小的可能，
                比如如果(pre+vis[i+1])*2就等于n，也就意味着本初字符串t的第一个字符可以随意选择，
                前面对vis这个向量的作用理解了的话，说的这应该懂了
                */
                ans[i] = static_cast<char>(j + 'a');//static_cast是静态类型转换
                pre += count[i][j];//累加当前位置 i 处字符 j 的出现次数
                break;//找到最小符合的，就跳出
            }
        }
    }

    return ans;
}

int main() {
    int t;
    cin >> t;
    for (int i = 0; i < t; i++) {
        string s;
        cin >> s;
        int n = s.length();//字符串s的长度
        for (int j = 1; j <= n; j++) {
            if (n % j == 0) {//找出字符串长度的因子，传入find函数
                string ans = find(s, j);
                if (!ans.empty()) {
                    cout << ans << endl;
                    break;
                }
            }
        }
    }
    return 0;
}

C:

#include<stdio.h>
#include<string.h>
#define MAXSIZE 200000
char s[MAXSIZE]={'\0'};
char ans[MAXSIZE]={'\0'};
void find(int n)
{
    int len=strlen(s);
    int a[n][30];
    memset(a,0,sizeof(a));//没想到二维数组也可以这样初始化
    int vis[n+1];
    memset(vis,0,sizeof(vis));
    for(int i=0;i<len;i++)
    {
        a[i%n][s[i]-'a']++;
    }
    for(int i=n-1;i>=0;i--)
    {
        for(int j=0;j<26;j++)
        {
            vis[i]=vis[i]>(vis[i+1]+a[i][j])?vis[i]:(vis[i+1]+a[i][j]);
        }
    }
    if(vis[0]*2<len)
        return;
    int pre=0;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<26;j++)
        {
            if((pre+a[i][j]+vis[i+1])*2>=len)
            {
                ans[i]=j+'a';
                pre+=a[i][j];
                break;
            }
        }
    }
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%s",s);
        int len=strlen(s);
        for(int i=1;i<=len;i++)
        {
            if(len%i==0)
            {
                memset(ans,'\0',sizeof(ans));
                find(i);
                if(strlen(ans)!=0)//判断是否为空
                {
                 printf("%s\n",ans);
                 break;                    
                }

            }
        }
    }
    return 0;
}