李沐动手学深度学习V2-双向循环神经网络Bidirectional RNN和代码实现

一. 双向循环神经网络和代码实现

1. 介绍

在序列学习中，以往假设的目标是：在给定观测的情况下（例如在时间序列的上下文中或在语言模型的上下文中），对下一个输出进行建模，虽然这是一个典型情景，但不是唯一的，例如我们考虑以下三个在文本序列中填空的任务：

我___。
我___饿了。
我___饿了，我可以吃半头猪。

根据可获得的信息量，我们可以用不同的词填空，如“很高兴”（“happy”）、“不”（“not”）和“非常”（“very”）。很明显每个短语的“下文”传达了重要信息（如果有的话），而这些信息关乎到选择哪个词来填空，所以无法利用这一点的序列模型将在相关任务上表现不佳。
例如如果要做好命名实体识别（例如，识别“Green”指的是“格林先生”还是绿色），不同长度的上下文范围重要性是相同的。

2. 双向模型

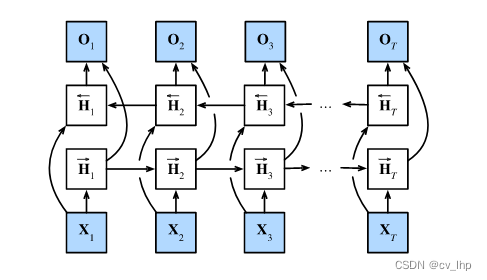
在前向模式下“从第一个词元开始运行”的循环神经网络，同时需要增加一个“从最后一个词元开始从后向前运行”的双向循环神经网络，下图所示描述了具有单个隐藏层的双向循环神经网络的架构。

3. 定义

对于任意时间步 $t$ ，给定一个小批量的输入数据 $\mathbf{X}_t \in \mathbb{R}^{n \times d}$ （样本数： $n$ ，每个示例中的输入数： $d$ ），并且令隐藏层激活函数为 $\phi$ 。在双向架构中，我们设该时间步的前向和反向隐状态分别为 $\overrightarrow{\mathbf{H}}_t \in \mathbb{R}^{n \times h}$ 和 $\overleftarrow{\mathbf{H}}_t \in \mathbb{R}^{n \times h}$ ，其中 $h$ 是隐藏单元的数目。前向和反向隐状态的更新如下：
$\begin{aligned} \overrightarrow{\mathbf{H}}_t &= \phi(\mathbf{X}_t \mathbf{W}_{xh}^{(f)} + \overrightarrow{\mathbf{H}}_{t-1} \mathbf{W}_{hh}^{(f)} + \mathbf{b}_h^{(f)}),\\ \overleftarrow{\mathbf{H}}_t &= \phi(\mathbf{X}_t \mathbf{W}_{xh}^{(b)} + \overleftarrow{\mathbf{H}}_{t+1} \mathbf{W}_{hh}^{(b)} + \mathbf{b}_h^{(b)}), \end{aligned}$
其中，权重 $\mathbf{W}_{xh}^{(f)} \in \mathbb{R}^{d \times h}, \mathbf{W}_{hh}^{(f)} \in \mathbb{R}^{h \times h}, \mathbf{W}_{xh}^{(b)} \in \mathbb{R}^{d \times h}, \mathbf{W}_{hh}^{(b)} \in \mathbb{R}^{h \times h}$ 和偏置 $\mathbf{b}_h^{(f)} \in \mathbb{R}^{1 \times h}, \mathbf{b}_h^{(b)} \in \mathbb{R}^{1 \times h}$ 都是模型参数。
接下来，将前向隐状态 $\overrightarrow{\mathbf{H}}_t$ 和反向隐状态 $\overleftarrow{\mathbf{H}}_t$ 连接起来，获得需要送入输出层的隐状态 $\mathbf{H}_t \in \mathbb{R}^{n \times 2h}$ 。在具有多个隐藏层的深度双向循环神经网络中，该信息作为输入(相当于当做 $X_{t}$ )传递到下一个双向层。
最后，输出层计算得到的输出为 $\mathbf{O}_t \in \mathbb{R}^{n \times q}$ （ $q$ 是输出单元的数目）：

$\mathbf{O}_t = \mathbf{H}_t \mathbf{W}_{hq} + \mathbf{b}_q.$

这里，权重矩阵 $\mathbf{W}_{hq} \in \mathbb{R}^{2h \times q}$ 和偏置 $\mathbf{b}_q \in \mathbb{R}^{1 \times q}$ 是输出层的模型参数。
事实上这两个方向可以拥有不同数量的隐藏单元，因为这两个方向的隐藏单元是拼接起来的而不是相加在一起。

4. 模型计算代价及其应用

双向循环神经网络的一个关键特性是：使用来自序列两端的信息来估计输出。也就是说使用来自过去和未来的观测信息来预测当前的观测，但是在对下一个词元进行预测的情况中，这样的模型并不是我们所需的。因为在预测下一个词元时，我们终究无法知道下一个词元的下文是什么，所以将不会得到很好的精度。具体地说在训练期间，我们能够利用过去和未来的数据来估计现在空缺的词；而在测试期间，我们只有过去的数据，因此精度将会很差，下面的训练和预测结果将说明这一点。
另一个严重问题是，双向循环神经网络的计算速度非常慢。其主要原因是网络的前向传播需要在双向层中进行前向和后向递归，并且网络的反向传播还依赖于前向传播的结果，因此梯度求解将有一个非常长的链。
双向层的使用在实践中非常少，并且仅仅应用于部分场合。例如，填充缺失的单词、词元注释（例如用于命名实体识别：当前词具有一词多意，需要结合上下文判断，或者判断当前词是名词还是动词）以及作为序列处理流水线中的一个步骤对序列进行编码（例如用于机器翻译）。

5. 双向循环神经网络的错误应用

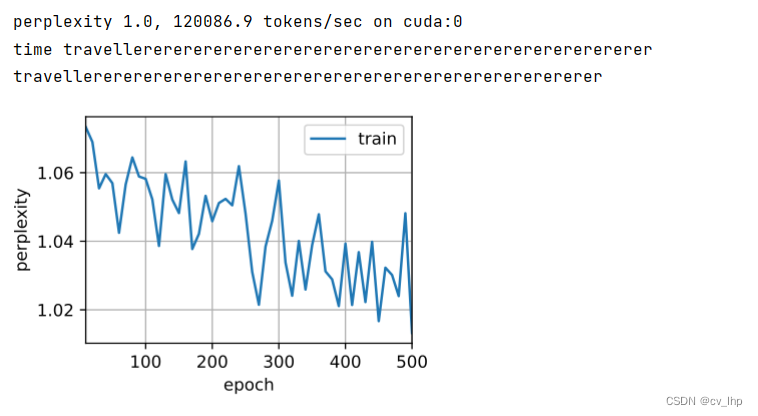
由于双向循环神经网络使用了过去的和未来的数据，所以我们不能盲目地将这一语言模型应用于任何预测任务。尽管模型训练出的困惑度是合理的，但该模型预测未来词元的能力却可能存在严重缺陷。用下面的代码进行预测当前词的下一个词为例进行引以为戒，以防在错误的环境中使用它们，训练和预测结果如下图所示：虽然训练结果的困惑度为1左右，但预测结果却是很差，很明显预测很差，没有预测出正确结果。双向循环神经网络的错误应用的全部代码如下：

import torch
import d2l.torch
from torch import nn
# 加载数据
batch_size,num_steps = 32,35
train_iter,vocab = d2l.torch.load_data_time_machine(batch_size,num_steps)
vocab_size,num_hiddens,device = len(vocab),256,d2l.torch.try_gpu()
input_size = vocab_size
num_layers = 2
#bidirectional=True表示使用双向的LSTM,num_layers=2表示网络有两层隐藏层,因此此模型为双向深度LSTM循环神经网络
deep_lstm = nn.LSTM(input_size,num_hiddens,num_layers=num_layers,bidirectional=True)
model = d2l.torch.RNNModel(deep_lstm,vocab_size)
model = model.to(device)
# 训练模型
num_epochs,lr = 500,1
d2l.torch.train_ch8(model,train_iter,vocab,lr,num_epochs,device,use_random_iter=False)

双向深度LSTM模型训练和预测结果

6. 李宏毅机器学习对双向循环神经网络的讲解

Bidirectional RNN

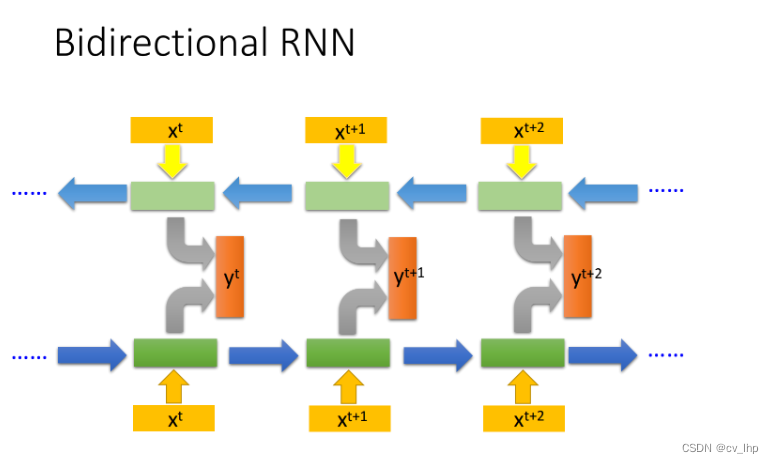
RNN 还可以是双向的，你可以同时训练一对正向和反向的RNN，把它们对应的hidden layer $x^t$ 拿出来拼接在一起，作为输入都接给一个output layer，然后得到最后的 $y^t$ ，如下图所示。

使用Bi-RNN的好处是，NN在产生输出的时候，它能够看到的范围是比较广的，RNN在产生 $y^{t+1}$ 的时候，它不只看了从句首 $x^1$ 开始到 $x^{t+1}$ 的输入，还看了从句尾 $x^n$ 一直到 $x^{t+1}$ 的输入，这就相当于RNN在看了整个句子之后，才决定每个词汇具体要被分配到哪一个槽中，这会比只看句子的前一半效果要更好。
Bidirectional RNN

7. 小结

在双向循环神经网络中，每个时间步的隐状态由当前时间步的前后数据同时决定。
双向循环神经网络主要用于序列编码和给定双向上下文的观测估计。
由于梯度链更长，因此双向循环神经网络的训练代价非常高。
将前向隐状态 $\overrightarrow{\mathbf{H}}_t$ 和反向隐状态 $\overleftarrow{\mathbf{H}}_t$ 连接起来，获得需要送入输出层的隐状态 $\mathbf{H}_t \in \mathbb{R}^{n \times 2h}$ 。在具有多个隐藏层的深度双向循环神经网络中，该信息作为输入(相当于当做 $X_{t}$ )传递到下一个双向层。

8. 链接