代价函数
J ( θ ) = J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( θ 0 + θ 1 x ( i ) − y ( i ) ) 2 J(\theta) = J(\theta_{0}, \theta_{1}) = \cfrac{1}{2m} \sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right)^{2}} = \cfrac{1}{2m} \sum\limits_{i = 1}^{m}{\left(\theta_{0} + \theta_{1} x^{(i)} - y^{(i)}\right)^{2}} J(θ)=J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2=2m1i=1∑m(θ0+θ1x(i)−y(i))2
梯度下降
Δ θ j = ∂ ∂ θ j J ( θ 0 , θ 1 ) \Delta{\theta_{j}} = \cfrac{\partial}{\partial{\theta_{j}}} J(\theta_{0}, \theta_{1}) Δθj=∂θj∂J(θ0,θ1)
θ j : = θ j − α Δ θ j = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_{j} := \theta_{j} - \alpha \Delta{\theta_{j}} = \theta_{j} - \alpha \cfrac{\partial}{\partial{\theta_{j}}} J(\theta_{0}, \theta_{1}) θj:=θj−αΔθj=θj−α∂θj∂J(θ0,θ1)
$$
\left[
\begin{matrix}
\theta_{0} \
\theta_{1}
\end{matrix}
\right] :=
\left[
\begin{matrix}
\theta_{0} \
\theta_{1}
\end{matrix}
\right] -
\alpha
\left[
\begin{matrix}
\cfrac{\partial{J(\theta_{0}, \theta_{1})}}{\partial{\theta_{0}}} \
\cfrac{\partial{J(\theta_{0}, \theta_{1})}}{\partial{\theta_{1}}}
\end{matrix}
\right]
$$
$$
\begin{aligned}
\left[
\begin{matrix}
\cfrac{\partial{J(\theta_{0}, \theta_{1})}}{\partial{\theta_{0}}} \
\cfrac{\partial{J(\theta_{0}, \theta_{1})}}{\partial{\theta_{1}}}
\end{matrix}
\right] &=
\left[
\begin{matrix}
\cfrac{1}{m} \sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right)} \\
\cfrac{1}{m} \sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right) x^{(i)}}
\end{matrix}
\right] =
\left[
\begin{matrix}
\cfrac{1}{m} \left(e^{(1)} + e^{(2)} + \cdots + e^{(m)}\right) \\
\cfrac{1}{m} \left(e^{(1)} x^{(1)} + e^{(2)} x^{(2)} + \cdots + e^{(m)} x^{(m)}\right)
\end{matrix}
\right] \\ &=
\cfrac{1}{m}
\left[
\begin{matrix}
1 & 1 & \cdots & 1 \\
x^{(1)} & x^{(2)} & \cdots & x^{(m)}
\end{matrix}
\right]
\left[
\begin{matrix}
e^{(1)} \\
e^{(2)} \\
\vdots \\
e^{(m)}
\end{matrix}
\right] \\ &=
\cfrac{1}{m} X^{T} e = \cfrac{1}{m} X^{T} (X \theta - y)
\end{aligned}
$$
Δ θ = 1 m X T e \Delta{\theta} = \cfrac{1}{m} X^{T} e Δθ=m1XTe
θ : = θ − α Δ θ = θ − α 1 m X T e \theta := \theta - \alpha \Delta{\theta} = \theta - \alpha \cfrac{1}{m} X^{T} e θ:=θ−αΔθ=θ−αm1XTe
Python实现
# -*- coding: utf-8 -*-
# @Time : 2024/12/19 1:25
# @Author : 从心
# @File : linear_regression_gradient_descent.py
# @Software : PyCharm
import numpy as np
import matplotlib.pyplot as plt
x = np.array([4, 3, 3, 4, 2, 2, 0, 1, 2, 5, 1, 2, 5, 1, 3])
y = np.array([8, 6, 6, 7, 4, 4, 2, 4, 5, 9, 3, 4, 8, 3, 6])
m = len(x)
x = np.c_[np.ones((m, 1)), x]
y = y.reshape(m, 1)
alpha = 0.01
iter_cnt = 1000
cost = np.zeros(iter_cnt)
theta = np.zeros((2, 1))
for i in range(iter_cnt):
h = x.dot(theta)
error = h - y
cost[i] = 1 / (2 * m) * error.T.dot(error)
# cost[i] = 1 / (2 * m) * np.sum(np.square(error))
delta_theta = 1 / m * x.T.dot(error)
theta -= alpha * delta_theta
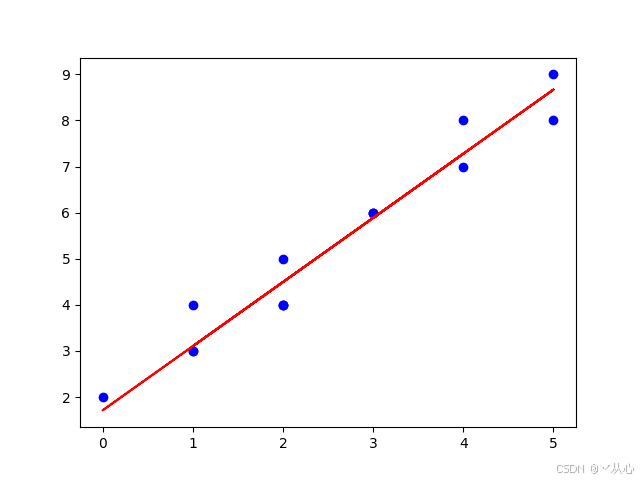
plt.scatter(x[:, 1], y, c='blue')
plt.plot(x[:, 1], h, 'r-')
plt.savefig('../visualization/fit.png')
plt.show()
plt.plot(cost)
plt.savefig('../visualization/cost.png')
plt.show()