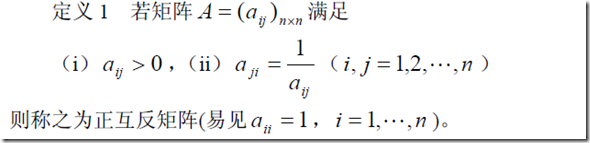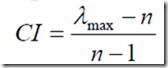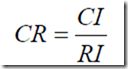概念:
层次分析法(Analytic Hierarchy Process ,简称 AHP )是对一些较为复杂、较为模糊的问题作出决策的简易方法,它特别适用于那些难于完全定量分析的问题。它是美国运筹学家T. L. Saaty 教授于上世纪 70 年代初期提出的一种简便、灵活而又实用的多准则决策方法
一、步骤
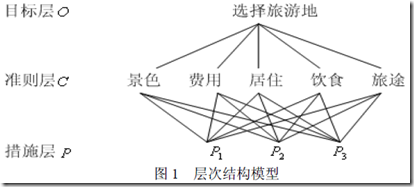
1、建立递阶层次结构模型
2、构造出各层次中的所有判断矩阵
3、层次单排序及一致性检验
4、层次总排序及一致性检验
二、递阶层次的建立与特点
1、分层:
(1)最高层:这一层次中只有一个元素,一般它是分析问题的预定目标和理想结果。
(2)中间层:这一层次中包含为了实现目标所涉及的中间环节,主要是一些考虑指标和一些准则。
(3)最底层:这一层次中包含为了实现目标可供选择的各种方案。
2、注意点:
一般不要1层不要超过9个因素
3、一个demo
二、构造判断矩阵
由于准则层中的各准侧的权值可能不同,所以应该设置一个权重。
1、比较判别矩阵的元素意义
设现在要比较n个因子对某因素Z的影响大小,采用两两比较建立比较判别矩阵
,xi与xj对Z的影响之比为aij。然后反过来xj与xi的影响之比为aji=1/aij。
2、比较判别矩阵的定义
3、关于比较判别矩阵元素的确定
使用数字1-9以及其倒数作为标度。
三、层次单排序及一致性检验
1、原理
判断矩阵A对应于最大特征值得特征向量W,经归一化即为同一层次相应元素对于上一层次元素相对重要性的排序权值。称为层次单排序
因此,我们通过来检验A是否为一致矩阵,当
比n大的越多,A的非一致性程度也就越严重,所以我们可以通过这种方法来检验一致性。
2、步骤
(1)计算一致性指标CI
(2)查询平均随机一致性指标RI,对应n=1到9,RI值分别为
这是通过随机的方法生成的一组标准指标。
(3)计算一致性比例CR
当CR<0.1,认为矩阵的一致性是可以接受的。
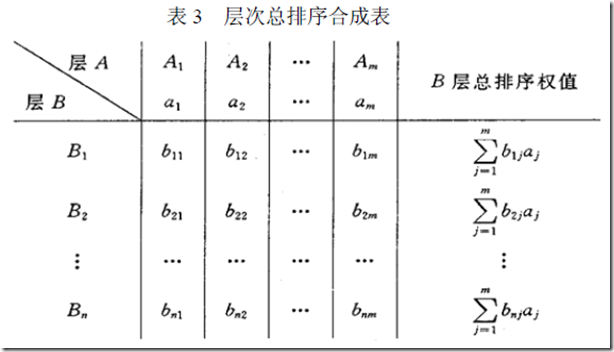
四、层次总排序及一致性检验
1、说明
(1)A为上一层次(高的层次),B为当前层次
(2)a1,a2,a3……am为A层次的总排序权重。
(3)b1j……bnj是B层对Aj的单排序权重。
(4)从最高层到最底层
现求B层中各因素关于总目标的权重,即求B层各因素的层次总排序权重b1,b2……bn。就按照上图中的方法进行计算。
2、然后对于层次总排序也要进行一致性检验。
当CR<0.10,认为层次总排序结果具有较满意的一致性并接受该分析结果。
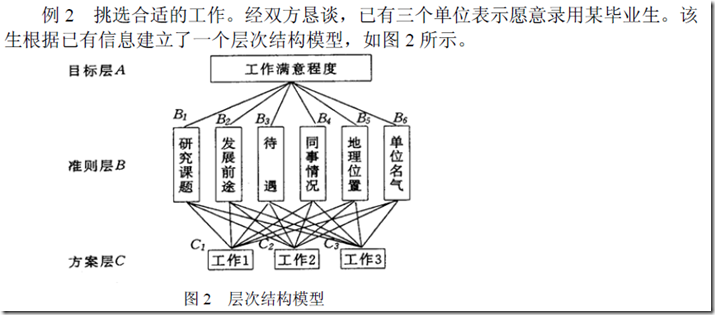
(二)层次分析法的应用
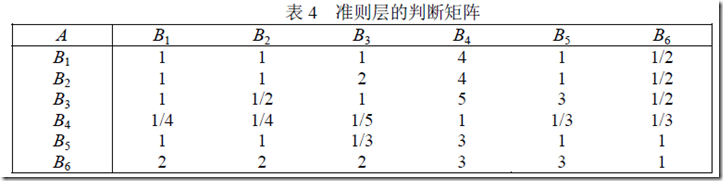
1、准则层的排序矩阵
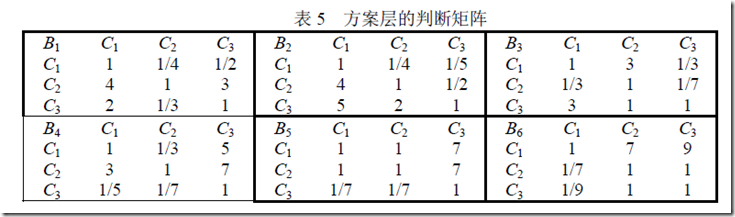
2、方案层的排序矩阵
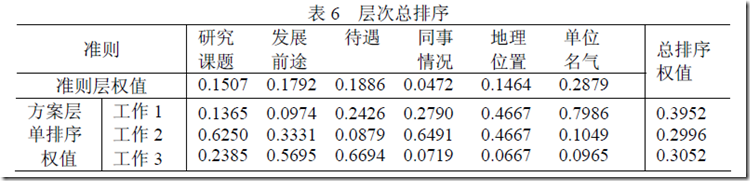
3、层次排序总结果
所以最满意的工作是1。