Algorithms practice:leetcode33 Search in Rotated Sorted Array
Description
There is an integer array ,nums, sorted in ascending order (with distinct values).
Prior to being passed to your function, nums is possibly rotated,at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated, at pivot index 3 and become [4,5,6,7,0,1,2].
Given the array nums, after the possible rotation ,and an integer target, we need to return ,the index of the target ,if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.
Example
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
Example 3:
Input: nums = [1], target = 0
Output: -1
Constraints
Constraints:
1 <= nums.length <= 5000
-104 <= nums[i] <= 104
All values of nums are unique.
nums is an ascending array that is possibly rotated.
-104 <= target <= 104
code
class Solution {
public:
int search(vector<int>& nums, int target) {//O(N) O(log(n))
int left =0;
int right = nums.size()-1;
while(left<=right)
{
int mid = (left+right)/2;
if (nums[mid] == target)
{
return mid;
}
if(nums[left] <=nums[mid]) // [left , mid] order subarray
{
if(nums[left] <=target && target< nums[mid])
{
right = mid-1;
}
else//( target> nums[mid] || target< nums[right])
{
left = mid+1;
}
}
else
{
// [mid , right] order subarray
if(nums[mid] <target && target<= nums[right])
{
left = mid+1;
}
else //( target> nums[mid] || target< nums[right])
{
right = mid-1;
}
}
}
return -1;
}
};
讲稿
today we talk about leetcode33 Search in Rotated Sorted Array.
here is a problem.
读完题之后
The first time I was reading the question, to be honest, I didn’t understand the question. Because it is confusing, and it’s not your fault to not understand this question. Why are we getting this confusing question in interviews? Why are interviewers trying to give us a hard time? the Interview is mock working senario, and we are getting confusing and complex requirements all the time, we should be capable of getting useful information from the complex conditions and able to solve the problem with code.
So let’s take a look together, and to find out which part is confusing, and what the question is really asking for.
For this question,The keyword is “rotate”, and it tells us how to rotate with the formula.
So let’s try an example with numbers.
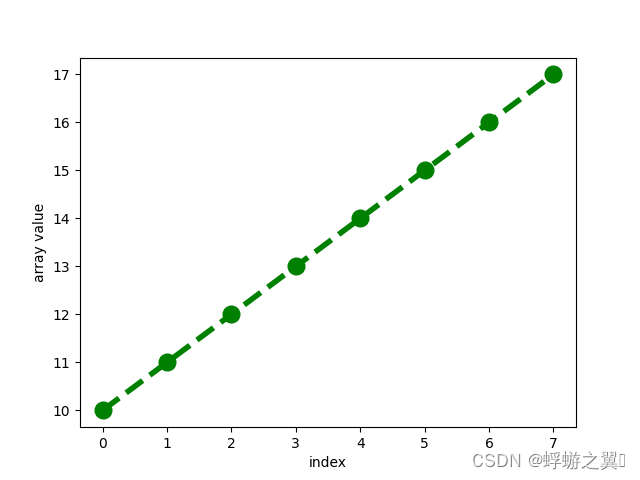
the original array is [10,11,12,13,14,15,16,17]
look at this picture: the vertical axis represents elements in array while the horizontal axis represents indexs of the elements.
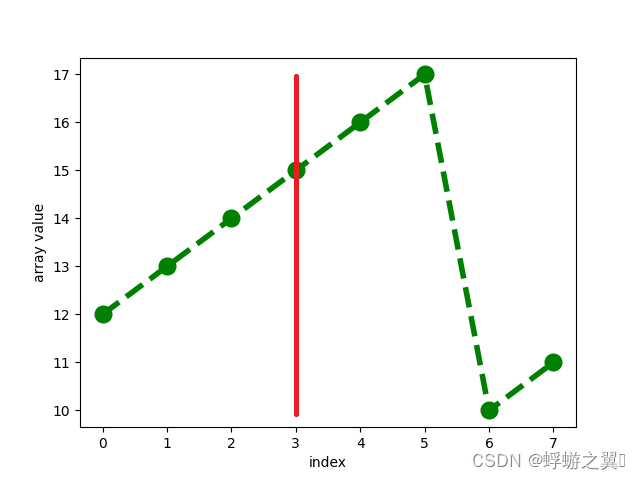
Suppose the pivot index is 3, We cut the array at pivot 3, move the left part to the end of the array. then, we get rotated array at pivot index 3 :
[13,14,15,16,17, 10,11,12]
here I list all rotated arrays with pivot from 0 to 7.
If the pivot index is zero then the array Doesn’t change/Remains the same.
so now you guys must know what rotating an array means.
as I mentioned before, the pivot can be any number from 0 to 7.
If the pivot is 1 then the rotated array looks like this.
If the pivot is 2 then the rotated array looks like this.
If the pivot is 3 then the rotated array looks like this.
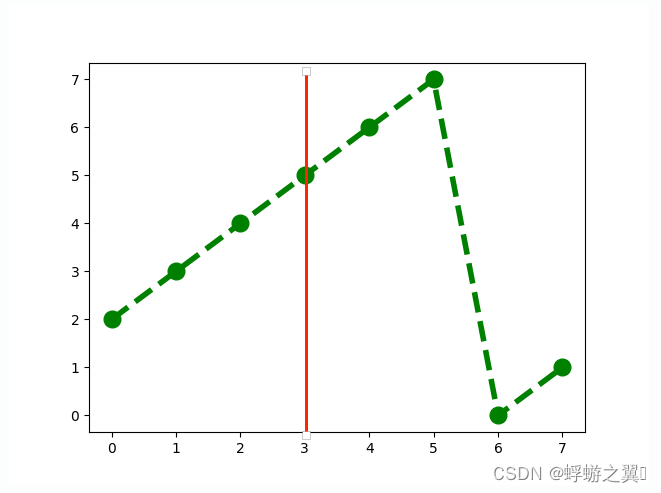
If the pivot is 4 then the rotated array looks like this.
If the pivot is 5 then the rotated array looks like this.
If the pivot is 6 then the rotated array looks like this.
If the pivot is 7 then the rotated array looks like this.
the next step is to think about what algorithm we want to use to solve the problem. my first thought is to figure out what the pivot is and that requires a linear search.but the time complexity will be O(n), it fails to fulfill the requirment. And the time complexity of binary search is O(logn), so I want to try binary search next.
let me give you an example.
the vertical axis represents elements in array while the horizontal axis represents indexs of the elements.
The main idea is to divide the search space into two halves from the middle . If the middle element is the target, the process terminates. If not, we decide which subarray to continue the search in (If not, we decide in which sub-array to continue the search.). The key to the problem is how to choose the subarray.
Here whole array is not sorted but we can figure out 2 sorted halves. one half of the array (either the left or the right) will always be sorted. We just have to identify the sorted half and eliminate the other half
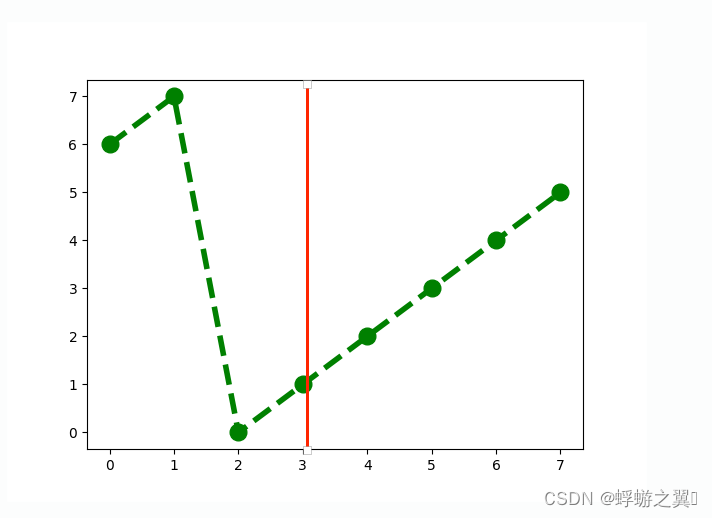
Now please take a closer look at this picture now I’m going to split the rotated array in half.
we can see the pivot index k = 2 and nums is [12,13,14,15,16,17, 10,11]
, and the target is 13, Now let’s try to split this rotated array in half from the middle.
we select index 3 as the middle element.
The sub-array on the left is [12 13 14 15], and the sub-array on the right is [16 17 10 11].
The left sub-array is in ascending order, and first we determine if the target is in this array.
if target >= nums[left] and target =< nums[middle]
if the target is larger than or equals nums[left] and smaller than or equals nums[middle], then we know the target can be found in this subarray.
In this case, our target is 13, which satisfies the conditions 12<13 and 13<15. Therefore, the target must be in this sub-array. So, we use this sub-array in the next iteration. Sometimes the target is not in the left subarray. in that case, we use the right sub-array in the next iteration. We will talk about what to do in that case later.
now we write the code:
firstly, we declare two int variables as Pointers: a left pointer and a right pointer and assign 0 to the left pointer ,assign nums.size()-1 to the right pointer .
int left =0;
int right = nums.size()-1;
we use while loop. In each iteration , we first need to calculate the middle pointer as (left +right )/2 (divided by 2). If the middle element is the target, we return the index of the middle element. if not, we search the target in the subarray in asending order. how do we determine which one that is?
while(left<=right)
{
int mid = (left+right)/2;
if (nums[mid] == target)
{
return mid;
}
....
}
}
we first check the left one.
if nums[left] <=nums[mid], then we know the elements in the left subarray are in asending order.
the next step is to check if the target is in it. If it is,We are gonna use the left subarray in the next iteration.
that means we no longer need the right subarray, we can get rid of it by assign mid -1 to the right pointer.
if(nums[left] <=nums[mid]) // [left , mid] order subarray
{
if(nums[left] <=target && target< nums[mid])
{
right = mid-1;
}
else//( target> nums[mid] || target< nums[right])
{
left = mid+1;
}
}
if the target is not in the left subarray, Then it must be in the right one. that means we don’t need the left subway. so how do we get rid of it? (问)
we can get rid of it by assign mid+1 to the right pointer.
In the scenario we just discussed, the left subarray is in Ascending order, Now let’s talk about what to do if the right sub array is in Ascending order.
else
{
// [mid , right] order subarray
if(nums[mid] <target && target<= nums[right])
{
left = mid+1;
}
else //( target> nums[mid] || target< nums[right])
{
right = mid-1;
}
the next step is to check if the target is in it. if the target is larger than or equals nums[mid] and smaller than or equals nums[right], then we know the target can be found in this subarray. We are gonna use the right subarray in the next iteration.
that means we no longer need the left subarray, we can get rid of it by assign mid +1 to the left pointer.
if the target is not in the right subarray, Then it must be in the left one. that means we no longer need the right subway.
we can get rid of it by assign mid-1 to the right pointer.
// [mid , right] order subarray
if(nums[mid] <target && target<= nums[right])
{
left = mid+1;
}
else //( target> nums[mid] || target< nums[right])
{
right = mid-1;
}
if the target is not in nums array, then we return -1 at the end.
that’s how we solve the problem.
It takes a while to clear your thought and find the correct solution. It’s not hard, but takes practice.
words
已整理
-
integer [ˈɪntɪdʒə]: In mathematics, an integer is an exact whole number such as 1, 7, or 24 as opposed to a number with fractions or decimals.
In C++, there are different types of variables (defined with different keywords), for example:
int - stores integers (whole numbers), without decimals, such as 123 or -123
double - stores floating point numbers, with decimals, such as 19.99 or -19.99 -
array [əreɪ]: An array of objects is a collection of them that is displayed or arranged in a particular way.
eg: Arrays are used to store multiple values in a single variable, instead of declaring separate variables for each value.(C++ https://www.w3schools.com/cpp/cpp_arrays.asp) -
ascending [əˈsɛndɪŋ] : If a group of things is arranged in ascending order, each thing is bigger, greater, or more important than the thing before it.
I shall list my objections to the plan in ascending order of importance.我将会把我反对这个计划的理由按重要性从小到大一一列出。 -
Descending [dɪˈsendɪŋ] :When a group of things is listed or arranged in descending order, each thing is smaller or less important than the thing before it.
The results, ranked in descending order (= from the highest to the lowest) are as follows: 结果按递减顺序排列如下。 -
distinct [dɪˈstɪŋkt]: values every element in the array is unique
C++ Program to Counting distinct elements in an array. -
Prior [ˈpraɪə®] :
未整理
Initialization is the process of assigning a value to the Variable. [2]
Declare and initialize a variable with an integer value [3]
binary search 二分搜索算法
terminate 终止(进程)
subarray
ascending
iteration迭代
pointer 指针
we declare two int variables 申明变量
assign 0 to left point 赋值
ascending order 升序排列
distinct values every element in the array is unique
柯林斯词典
Prior to v-ing
passed to your function 补充例句 pass by value 按值传参(补全)
resulting :
0-indexed: Zero-based numbering is a way of numbering in which the initial element of a sequence is assigned the index 0, rather than the index 1 as is typical in everyday non-mathematical or non-programming circumstances. Under zero-based numbering, the initial element is sometimes termed the zeroth element,[1] rather than the first element; zeroth is a coined ordinal number corresponding to the number zero. In some cases, an object or value that does not (originally) belong to a given sequence, but which could be naturally placed before its initial element, may be termed the zeroth element. There is not wide agreement regarding the correctness of using zero as an ordinal (nor regarding the use of the term zeroth), as it creates ambiguity for all subsequent elements of the sequence when lacking context.
Zero-based array indexing is a way of numbering the items in an array such that the first item of it has an index of 0, whereas a one-based array indexed array has its first item indexed as 1.
Prior to being passed to your function
equation
decide on: to choose someone or something from a number of possible choices
In these graphs, the vertical axis represents the position of the object while the horizontal axis represents the time elapsed: the dependent variable, position, depends on the independent variable, time.
link
https://leetcode.com/problems/search-in-rotated-sorted-array/description/
- C++ Variables
- https://www.learncpp.com/cpp-tutorial/variable-assignment-and-initialization/
- https://www.codeease.net/programming/python/Declaration-and-Initialization-of-Variables
- https://leetcode.com/problems/search-in-rotated-sorted-array/solutions/3879263/100-binary-search-easy-video-o-log-n-optimal-solution/
-1 negtive one
断句 <5词语, 一般动词加重
先将大框架,再一点点讲细节
读题框架
解题框架(算法)
在学生最少准备时,有所收获
我们将数字带入到公式中得到如下结果。(英语如何翻译?)
坐标的物理意义
变量的物理意义
- 看到题目:畏难,心理恐惧
- 看中文“旋转”,一下子就明白了,看英文有困难。理解英文困难