简单来讲,求解积分的过程实际上就是求导的逆过程,微分与积分互为互逆运算。
4.1.1 不定积分的概念
定义1 设函数f(x)是定义在区间I上的函数,若存在函数 F(x),对于任意x∈I都有F'(x)=f(x)或dF(x)=f(x)dx,则称F(x)是f(x)在区间I上的一个原函数
对于此概念需要注意的是,受制于常数项C,若有一个原函数F(x),原函数必然存在无穷多个原函数F(x)+C。
定义2 如果函数F(x)是函数f(x)在区间 I 上的一个原函数,则称f(x)的全体原函数的集合{F(x)+C|C∈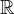
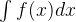
简记为
∫ 称为积分号,f(x)称为被积函数,x为积分变量,特别需要注意的是,从积分开始我们的运算将不仅仅限制于x的运算,被积变量见会出现多种不同的变量.
4.1.2可积的条件
定理1 如果f(x)在区间 I 上连续,那么f(x) I 上必然存在原函数,即连续函数必有原函数.
从定理1 我们可以看出,与可导的条件--光滑相比,积分运算的条件要更容易满足.
4.1.3积分的几何意义
称任一原函数的图像为被积函数的一条积分曲线,其全体原函数的图像称为被积函数的积分曲线簇,即积分的几何意义实际上是求出了原函数的一组图像。
4.1.4不定积分的性质
性质1 ![\left [ \int f(x)dx \right ]{}'=f(x)](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNsZWZ0JTIwJTVCJTIwJTVDaW50JTIwZiUyOHglMjlkeCUyMCU1Q3JpZ2h0JTIwJTVEJTdCJTdEJTI3JTNEZiUyOHglMjk%3D)
对积分进行求导会回到被积函数,对积分进行微分会回到被积函数,性质1实际上说明了积分与微分互为逆运算。
性质2 或
性质2的右侧公式实际上等价于,即以f(x)为积分变量对1求积分,这里就体现出了积分变量的多样化,因此在求解定积分的过程中,要关注积分变量。
性质3
性质4
由性质3和4我们可以得到更一般的结论
性质5
即
而这说明不定积分运算是一个线性运算。
4.1.5直接积分法
利用不定积分的定义求解不定积分往往并不方便,于是选择借助不定积分的性质和基本积分表,利用适当的数学运算求解不定积分,这种方法称为不定积分法。


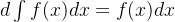
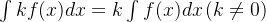
![\int \left [ \sum_{i=1}^{n} kifi(x)\right ]dx=\sum_{i=1}^{n}ki\left [ \int fi(x)dx \right ]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNpbnQlMjAlNUNsZWZ0JTIwJTVCJTIwJTVDc3VtXyU3QmklM0QxJTdEJTVFJTdCbiU3RCUyMGtpZmklMjh4JTI5JTVDcmlnaHQlMjAlNURkeCUzRCU1Q3N1bV8lN0JpJTNEMSU3RCU1RSU3Qm4lN0RraSU1Q2xlZnQlMjAlNUIlMjAlNUNpbnQlMjBmaSUyOHglMjlkeCUyMCU1Q3JpZ2h0JTIwJTVE)