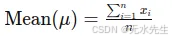一、说明
机器学习中的统计
随着我们深入研究机器学习领域,了解统计学在该领域的作用至关重要。统计学是机器学习的支柱,它提供了理解数据和获得有意义见解的工具和方法。在这篇文章中,我们将探讨统计的定义、它在机器学习中的重要性,以及描述性统计和推理统计之间的区别。
二、统计概述
统计学是数学的一个分支,涉及数据的收集、分析、解释、表示和组织。它提供了一个基于数据做出决策和预测的框架。在机器学习的背景下,统计学可以帮助我们理解我们正在处理的数据,准确地对其进行建模,并得出可靠的结论。
机器学习中的定义和重要性
统计学可以定义为从数据中学习的科学。它涉及设计实验和调查、收集数据、总结信息和进行推理的方法。在机器学习中,统计数据至关重要,因为:
-
数据理解:在构建任何机器学习模型之前,了解数据很重要。统计技术有助于汇总和可视化数据,揭示模式、异常和关系。
-
模型构建:统计模型构成了许多机器学习算法的基础。回归、分类和聚类等技术都源于统计方法。
-
模型评估:Statistics 提供指标和测试来评估机器学习模型的性能。这可确保模型可靠且预测准确。
-
推理和预测:通过统计推理,我们可以根据样本数据对总体进行预测。这在机器学习中进行预测或识别趋势时特别有用。
三、描述性统计与推断性统计
统计学大致可分为两种类型:描述性统计和推论统计。两者都在数据分析过程中发挥着重要作用,但它们的用途不同。
3.1 描述统计学
描述性统计总结并描述数据集的主要特征。它们提供有关样本和度量的简单摘要。这些摘要可以是图形或数字。以下是一些关键概念:
- 集中趋势的测量:这些值包括平均值 (平均值)、中位数 (中间值) 和众数 (最频繁的值),它们有助于识别数据集的中心。
- 离差度量: 这些指标包括范围(最大值和最小值之间的差值)、方差和标准差,它们表示数据中的散布或可变性。
- 数据可视化:直方图、箱形图和散点图等图形表示有助于可视化数据并识别模式或异常值。
描述性统计提供了一种以合理的方式简化大量数据的方法。每个描述性统计数据都将大量数据简化为更简单的摘要。
3.2 推论统计
描述性统计旨在总结手头的数据,而推论统计用于从数据样本中对更大的总体进行预测或推断。这包括:
- 采样:从总体中选择一个代表性群体,以得出有关整个总体的结论。
- 假设检验:对总体提出主张或断言,并通过数据分析检验这些主张。
- 置信区间: 提供可能包含相关群体参数的值范围。
- 回归分析:了解变量之间的关系并进行预测。
推论统计使我们能够对总体做出概率陈述,并了解与我们的结论相关的不确定性。
四、描述性统计中的均值、中位数和众数
在分析数据时,了解其中心趋势至关重要。集中趋势的度量提供表示数据集的中心点或典型值的单个值。三种最常见的度量是均值、中位数和众数。每个 Cookie 都提供了独特的见解,并在不同的上下文中非常有用。让我们深入研究这些度量中的每一个。
意味 着
平均值(通常称为平均值)是数据集中所有值的总和除以值的数量。它是一个度量值,它提供表示数据分布中心点的单个值。
均值公式:
这里:
xi 表示数据集中的每个值。
n 是数据集中值的数目。
示例:
考虑数据集:5、10、15、20、25
平均值 = (5 + 10 + 15 + 20 + 25) / 5 = 75/5 = 15
Python 代码:
import numpy as np
from scipy import stats
data = np.array([5, 10, 15, 20, 25])
# Calculate the mean
mean = np.mean(data)
print("Mean:", mean)
# Mean: 15.0
优点:
- 易于计算和理解。
- 使用所有数据点,提供全面的度量。
缺点:
- 对异常值敏感,异常值会显着扭曲平均值。
中位数
中位数是数据集的中间值,当值按升序或降序排列时。如果观测值数为偶数,则中位数是两个中间数字的平均值。
查找中位数的步骤:
1。按升序排列数据。
2. 确定中间值。
示例:
考虑数据集:5、10、15、20、25。
- 按升序排列(已完成): 5, 10, 15, 20, 25
2.中间值(中位数)为 15。
python 中的代码:
import numpy as np
from scipy import stats
data = np.array([5, 10, 15, 20, 25])
# Calculate the median
median = np.median(data)
print("Median:", median)
# Median: 15.0
注意: 对于偶数个观测值,请考虑数据集:5、10、15、20。
- 按升序排列: 5, 10, 15, 20
2.中间值为 10 和 15。 - 中位数 = (10 + 15) / 2 = 12.5
优点:
- 不受异常值的影响,使其成为集中趋势的稳健衡量标准。
- 在偏态分布中更准确地反映数据集的中心。
缺点:
- 没有利用所有数据点,可能会忽略有价值的信息。
模式
mode 是数据集中出现频率最高的值。数据集可能具有一种模式、多个模式,或者如果没有数字重复,则根本没有模式。
示例:
考虑数据集:5、10、15、20、20、25
- 模式为 20,因为它出现得最频繁。
python 中的代码:
import numpy as np
from scipy import stats
data = np.array([5, 10, 15, 20, 25])
# Calculate the mode
mode = stats.mode(data)
print("Mode:", mode.mode)
# Mode: 5
优点:
- 易于识别。
- 对于我们希望了解最常见类别的分类数据很有用。
缺点:
- 可能不是唯一的;多种模式会使解释复杂化。
- 并不总是代表数据集,尤其是连续数据。
选择正确的度量
- 平均值:非常适合没有异常值的对称分布。
- 中位数:最适合偏态分布或具有异常值的数据。
- 模式: 对于分类数据以及识别数据集中最常见的值非常有用。
了解这些集中趋势的度量对于任何数据分析都至关重要,为更高级的统计技术和数据驱动的决策奠定了基础。通过选择合适的度量,您可以更好地解释数据并提取有意义的见解。
在我们的机器学习之旅中,我们在第 33 期中探讨了集中趋势的测量。