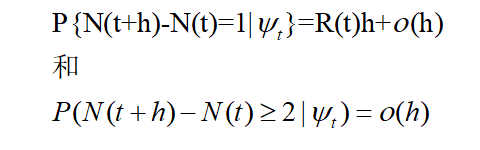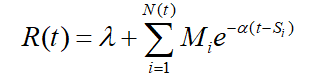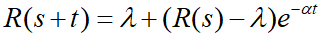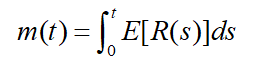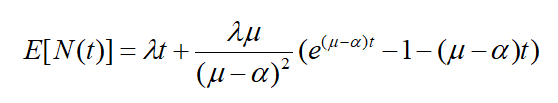• 最近由于项目需要，需要了解下hawkes过程相关理论，可是在百度或者其他搜索引擎上却搜索不到相关内容，倒是搜出来不少有关文章，可是大都是基于hawkes理论的应用。于是下面是我对hawkes过程的介绍：
  • 不同于非时齐的泊松（Possion）过程的强度函数$\lambda$(t)是个确定的函数，存在计数过程在时刻t强度函数{N(t),t>=0}的值，记为，它是个随机变量，其值依赖于直至时刻t的过程的历史。也就是说，若将直至时刻t的过程的历史记为$\psi$t，则在时刻t的强度率是一个随机变量，其值由所确定，且使
    
  • hawkes过程是具有随机强度函数的计数过程的例子之一。这种计数过程假定了存在一个基本的强度值$\lambda$>0，且对每个事件附以一个称为标志值的非负的随机变量，其值独立于以前发生的一切事件，且具有分布F。假定每当一个事件发生时，随机强度函数的当前值就增加了这个事件的标志值得量，且这个增加的量以指数速率按时间递减。更确切地，若到时刻t为止，已发生事件的总数为N(t)，事件的发生时间S1<S2<…<SN(t)，记第i个事件的标志值为Mi,i=1,…,N(t),则
    
  • 换句话说，hawkes过程是满足如下条件的计数过程：
  • 1.R(0)=$\lambda$;
  • 2.每当一个事件发生时，过程的随机强度增加一个等于此事件的标准值得量；
  • 3.若在s和s+t之间没有事件发生，则
• 因为每当一个事件发生时强度增加，所以称hawkes过程为自激过程。
• 下面介绍两条引理：
• 1.满足N(0)=0的计数过程N(t)，其随机强度函数为R(t)，记m(t)=E[N(t)]，则
  
• 2.若在hawkes过程中标志值的均值为$\mu$，则对此过程有