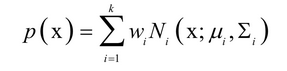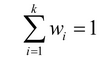高斯混合模型通过多个正态分布的加权和来描述一个随机变量的概率分布,概率密度函数定义为:
其中x为随机向量,k为高斯分布的个数,w(i)为权重,u为高斯分布的均值向量,E为协方差矩阵。所有权重之和为1,即:
任意一个样本可以看作是先从k个高斯分布中选择出一个,选择第i个高斯分布的概率为w(i),再由第i个高斯分布产生出这个样本数据x。高斯混合模型可以逼近任何一个连续的概率分布,因此可以看作是连续性概率分布的万能逼近器。之所以要保证权重的和为1,是因为概率密度函数必须满足在
的积分值为1。
指定高斯分布的个数,给定一组训练样本,可以通过期望最大化EM算法确定高斯混合模型的参数。每次迭代时,在E步计算期望值,在M步最大化期望值,如此循环交替。