python数据结构之栈和队列
3.1栈
3.1.1栈的定义
特点:
- 后进先出,先进后出
- 允许插入、删除的一端为栈顶,另一端为栈底
- 无元素为空栈
- 插入操作称为进栈或如栈,删除操作称为退栈或出栈
基本运算
empty():判断是否为空
push(e):将元素e插入作为栈顶元素
pop():出栈,返回栈顶元素
gettop():返回当前栈顶元素
3.1.2栈的顺序存储结构及其基本运算算法的实现
- 顺序存储结构
用列表data存放栈中元素,称为顺序栈,data[0]端为栈底,data[-1]端为栈顶,len(data)为栈中实际的元素个数
| 元素索引 | 0 | 1 | …… | i | …… | n-1 |
|---|---|---|---|---|---|---|
| data列表 | a0 | a1 | …… | a i | …… | an-1 |
栈底 top⬆️
- 顺序栈四要素
- 栈空:len(data)==o或者not data
- 栈满:不考虑
- 元素e进栈:将e加到栈顶
- 出栈:删除栈顶元素,返回该元素
- 顺序栈基本运算
#初始化
class SqStack:
def __init__(self):
self.data=[]
#判断栈是否为空
def empty(self):
if len(self.data)==0:
return True
return False
#进栈
def push(self,e):
self.data.append(e)
#出栈
def pop(self):
assert not self.empty()
return self.data.pop()
#取栈顶元素
def gettop(self):
assert not self.empty()
return self.data[-1]
3.1.3栈的链式存储结构
- 特点:
- 首结点是栈顶结点,尾结点是栈底结点
- 四要素:
- 栈空:head.next==None
- 栈满:不考虑
- 元素e进栈:将包含该元素的结点s插入,作为首结点
- 出栈:返回首结点值,并删除该结点
- 链栈基本运算
#初始化
class LinkNode():
def __init__(self,data=None):
self.data=data
self.next=None
class LinkList():
def __init__(self):
self.head=LinkNode()
self.head.next=None
#判断是否为空
def empty(self):
if self.head.next==None:
return True
return False
#进栈
def push(self,e):
p=LinkNode(e)
p.next=self.head.next
self.head.next=p
#出栈
def pop(self):
assert self.head.next!=None
p=self.head.next
self.head.next=p.next
return p.data
#取栈顶元素
def gettop(self):
assert self.head.next!=None
return self.head.next.data
3.2队列
3.2.1队列的定义
特点:
- 插入的一端称为队尾,进行删除的一端为队头或队首
- 插入新元素为进队或入队,新元素进队后就成为新的队尾元素
- 从队列删除元素为出队或离队,出队后其后继元素为新的队首元素
- 队列也称为先进先出表
基本运算
empty():判断是否为空
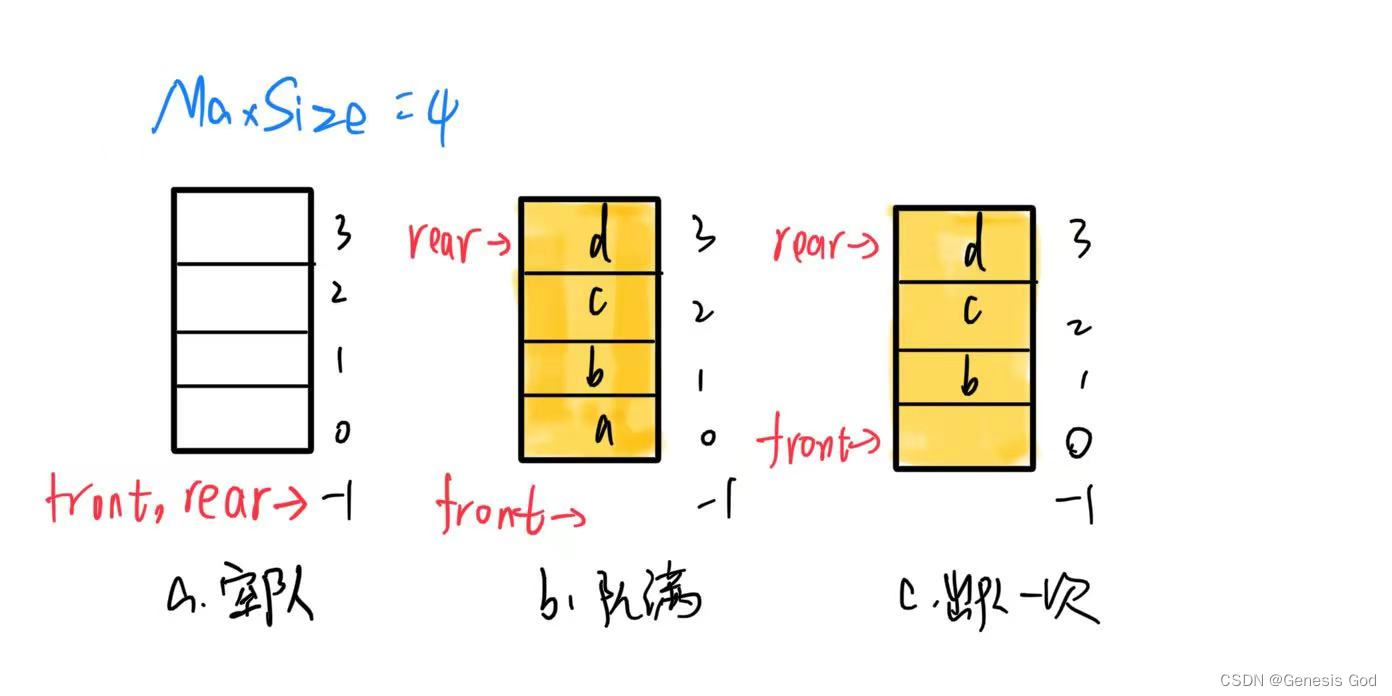
3.2.2队列的顺序存储结构及其基本运算算法的实现
- 顺序存储结构——顺序队
front:队头元素的前一个位置
rear:队尾元素的位置
| 数组下标 | 0 | …… | …… | MaxSize-1 | ||||
|---|---|---|---|---|---|---|---|---|
| data数组 | … | a0 | …… | a i | …… | an-1 | … |
⬆️ ⬆️
front rear
- 非循环队列
- 四要素:
- 队空条件:front==rear
- 队满条件:rear==MaxSize-1
- 元素e进队操作:队尾指针rear+1,然后将e放在该位置
- 出队操作:front+1,然后取出该位置的元素
- 基本运算
#初始化
MaxSize=100
class SqQueue:
def __init__(self):
self.data=[None]*MaxSize
self.front=-1
self.rear=-1
#判断是否为空
def empty(self):
return self.front==self.rear
#进队
def push(self,e):
assert not self.front==self.rear
self.rear+=1
self.data[self.rear]=e
#出队
def pop(self):
assert not self.empty()
self.front+=1
return self.data[self.front]
#取队头元素
def gethead(self):
assert not self.empty()
return self.data[self.front+1]
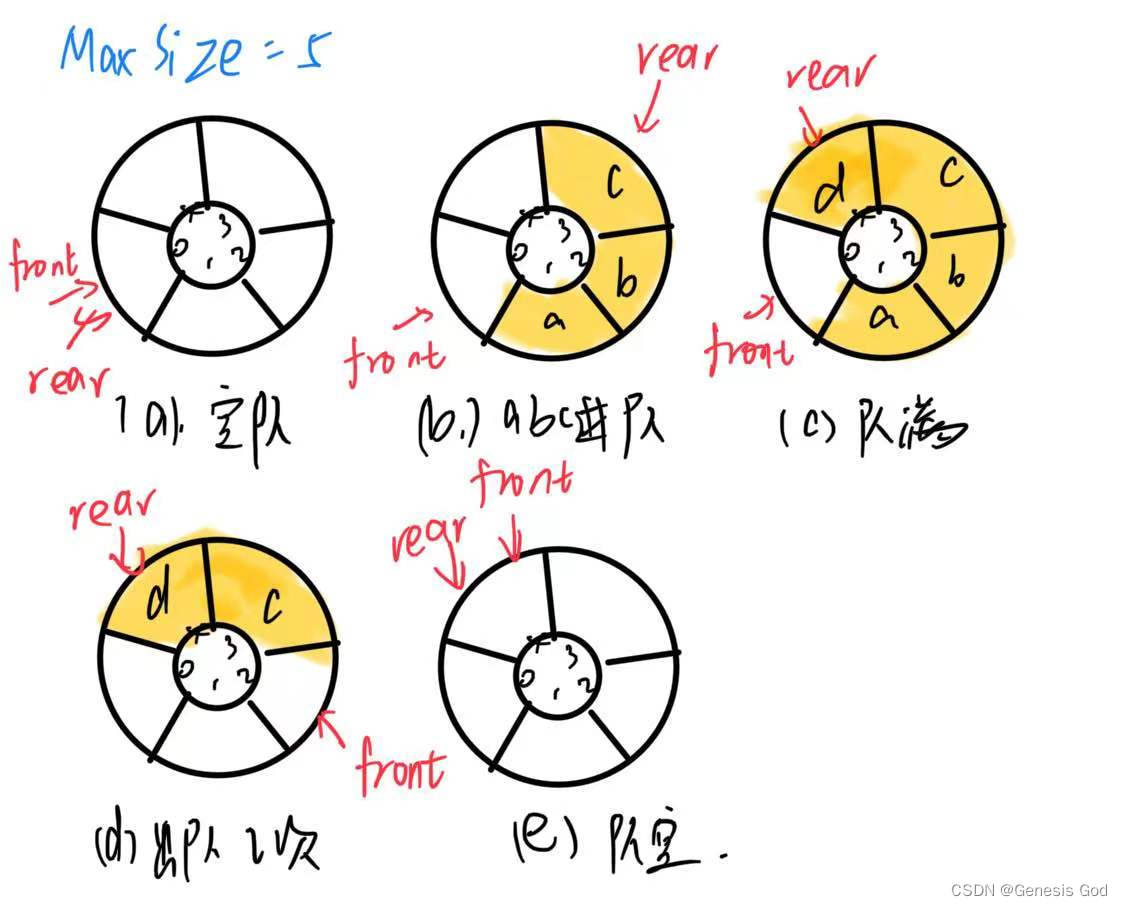
- 循环队列
- 特点:
- 队首指针循环进1,front=(front+1)%MaxSize
- 队尾指针循环进1,rear=(rear+1)%MaxSize
- 循环队列的队首与队尾指针初始化均为0,即front=rear=0
- 四要素:
- 队空条件:front==rear
- 队满条件:(rear+1)%MaxSize==front
- 元素e进队操作:rear=(rear+1)%MaxSize
- 出队操作:front=(front+1)%MaxSize
#初始化
MaxSize=100
class CSqQueue:
def __init__(self):
self.data=[None]*MaxSize
self.front=0
self.rear=0
#判断是否为空
def empty(self):
return self.front==self.rear
#进队
def push(self,e):
assert (self.rear+1)%MaxSize!=self.front
self.rear=(self.rear+1)%MaxSize
self.data[self.rear]=e
#出队
def pop(self):
assert not self.empty()
self.front=(self.front+1)%MaxSize
return self.data[self.front]
#取队头元素
def gethead(self):
assert not self.empty()
head=(self.front+1)%MaxSize
return self.data[head]
3.2.3队列的链式存储结构
- 特点
- 这里的单链表不带头结点
- 使用两个指针标识,front指向队头结点,rear指向队尾结点
- 用来存储单链表的的队列为链队
- 四要素
- 栈空:front=rear=None,可以仅以front=None表示
- 栈满:不考虑
- 元素e进队:将包含该元素的结点s插入到单链表尾部,并让队尾指针指向它
- 出队:取出队首结点的data值并将其从链队中删除
- 基本运算
#初始化
class LinkNode():
def __init__(self,data=None):
self.data=data
self.next=next
class LinkQueue():
def __init__(self):
self.front=None
self.rear=None
#判断是否为空
def empty(self):
return self.front==None
#进队
def push(self,e):
s=LinkNode(e)
if self.empty():
self.front=self.rear=s
else:
self.rear.next=s
self.rear=s
#出队
def pop(self):
assert not self.empty()
if self.front==self.rear:
e=self.front.data
self.front=self.rear=None
else:
e=self.front.data
self.front=self.front.next
return e
#取队头元素
def gethead(self):
assert not self.empty()
e=self.front.data
return e
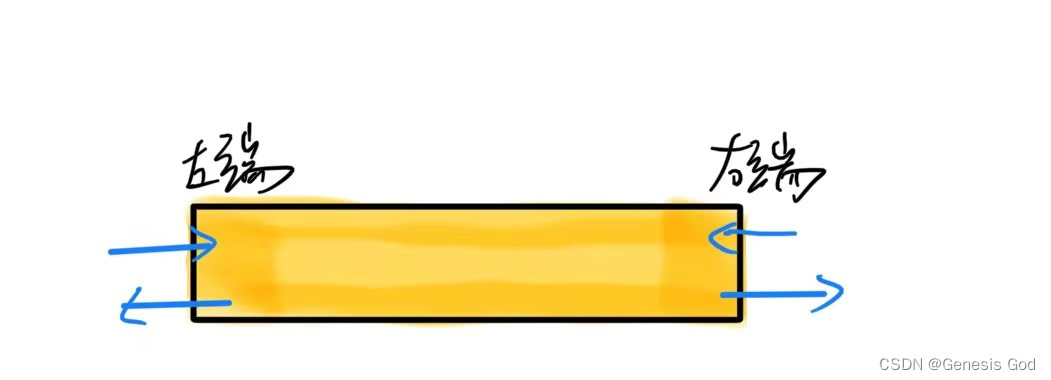
3.2.4 双端队列
- 特点
- 可以在两段进行进队和出队,具有队列和栈的特性
- double-ended queue简称deque,在collections集合里
- 创建双端队列
- 创建一个空双端队列
qu=deque() - 创建一个固定长度的双端队列
qu=deque(maxlen=N),此时qu为空,固定长度为N,当新的元素加入而双端队列满时,自动删除最老的元素 - 由一个列表元素创建一个双端队列
qu=deque(L),此时qu包含列表L中的元素
-
双端队列的方法
deque.clear():清除所有元素
deque.append(x):在队列右端添加x,时间复杂度O(1)
deque.appendleft(x):在队列左端添加x,时间复杂度O(1)
deque.pop():在队列右端出队一个元素,时间复杂度O(1)
deque.popleft():在队列左端出队一个元素,时间复杂度O(1)
deque.remove(x):在队列中删除首个和x匹配的元素,时间复杂度O(n)
deque.count(x):计算队列中元素为x的个数,时间复杂度O(n)
deque.extend(L):在队列右端添加列表L的元素
deque.entendleft(L):在队列左端添加列表L的元素
deque.reverse():逆置列表中所有元素
deque.rotate(n):移位,n为正,向右移,n为负,向左移 -
用双端队列实现栈
- 方法1:左端为栈底,右端为栈顶,append()为进栈方法,pop()为出栈方法
- 方法2: 左端为栈顶,右端为栈底,appendleft()为进栈方法,popleft()为出栈方法
例:
from collections import deque
st=deque()
st.append(1)
st.append(2)
st.append(3)
while len(st)>0:
print(st.pop(),end='')
print()
- 用双端队列实现普通队列
- 左端为队头(出队端),右端为队尾(进队端),用popleft()作为出队方法,append()作为进队方法
- 右端为队头(出队端),左端为队尾(进队端),用pop()作为出队方法,appendleft()作为进队方法
例:
from collections import deque
qu=deque()
qu.append(1)
qu.append(2)
qu.append(3)
while len(qu)>0:
print(qu.popleft(),end='')
print()