提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

一、什么是马尔科夫决策模型

   马尔科夫链是由俄罗斯数学家安德烈・马尔科夫（Andrey Markov）在 20 世纪初提出的。马尔科夫在研究随机过程时发现，某些随机过程具有一种特殊的性质，即未来的状态只取决于当前的状态，而与过去的历史无关，这就是著名的马尔科夫性质。
   马尔科夫决策模型（Markov Decision Process，MDP）是一种用于在不确定性环境下进行决策的数学框架，

二、马尔科夫决策的原理

   马尔科夫决策的核心公式是贝尔曼方程，其原理是基于马尔科夫性质构建动态决策框架，通过计算状态价值函数来确定最优策略，以实现长期累计奖励的最大化。以下是具体内容：
核心公式：贝尔曼方程
   V(s) = max_a∈A ∑_s’∈S P_ss’^a [R(s,a,s’) + γV(s’)]
其中：V (s) 表示状态 s 的价值函数，它代表从状态 s 出发，按照最优策略运行所能获得的长期累计奖励的期望。
a 是一个动作，A 是所有可能的动作的集合，即动作空间。
s’ 是系统在下一个时间步可能转移到的状态，S 是所有可能的状态的集合，即状态空间。
P_ss’^a 表示在当前状态 s 采取动作 a 的情况下，转移到下一个状态 s’ 的概率，即状态转移概率。
R (s,a,s’) 是奖励函数，表示在状态 s 采取动作 a 转移到状态 s’ 时所获得的奖励值。
γ 是折扣因子，是一个介于 0 和 1 之间的数，用于权衡未来奖励和当前奖励的重要性。
   马尔科夫性质：马尔科夫决策基于马尔科夫性质，即系统在未来时刻的状态仅取决于当前时刻的状态和所采取的动作，与过去的历史状态无关。用数学公式表示为：P (S_(t + 1)|S_t,A_t,S_(t - 1),A_(t - 1),…) = P (S_(t + 1)|S_t,A_t)。这一性质大大简化了对复杂系统的建模和分析，使得我们可以专注于当前状态和动作对未来状态的影响。

三、主要组成部分

1.状态空间

   系统所有可能处于的状态的集合，如机器人的不同位置、库存的不同水平等。不同的应用场景有不同的状态定义，它确定了模型中所有可能出现的情况。
动作空间：在每个状态下可以采取的动作的集合，例如机器人的移动方向、库存管理中的补货策略等。动作空间定义了决策者在每个状态下能够采取的行动，这些行动会影响系统的状态转移和最终的奖励。

2.状态转移概率

   描述了在特定状态下采取特定动作后，系统转移到其他各个状态的可能性。它是基于历史数据或对系统的理解而确定的，用于计算系统在不同决策下的状态变化情况。

3.奖励函数

   用于衡量系统在不同状态转移和动作下的收益或成本。通过奖励机制，模型可以引导智能体选择能够获得更高累计奖励的动作，以实现目标，如最大化利润、最小化成本等。

4.折扣因子

   随着时间步的推移，未来的奖励在当前决策中的重要性会逐渐降低，折扣因子就是用来体现这种时间价值的衰减。它使得模型更加关注近期的收益和决策效果，避免无限期地考虑未来奖励。

5.决策过程与目标

   在每个时间步 t，智能体处于当前状态 S_t，根据某种策略 π 选择一个动作 A_t。策略 π 是一个从状态到动作的映射，表示在不同状态下应采取的动作。然后系统根据状态转移概率 P_ss’^a 转移到下一个状态 S_(t + 1)，并获得相应的奖励 R_(t + 1)。智能体的目标是通过选择合适的策略 π，最大化长期累计奖励的期望，即 E [∑_(t = 0)^∞ γ^tR_(t + 1)]。

6.求解最优策略

   通过不断迭代贝尔曼方程来计算每个状态的价值函数 V (s)。在每次迭代中，对于每个状态 s，计算在不同动作 a 下的期望价值，即 ∑_s’∈S P_ss’^a [R (s,a,s’) + γV (s’)]，然后选择使期望价值最大的动作作为当前状态的最优动作，更新价值函数。经过多次迭代后，价值函数收敛，此时确定的动作策略即为最优策略。

四、马尔科夫决策的案例

1.案例背景

   假设一家电子产品零售商需要管理其智能手机的库存。市场需求存在不确定性，但可以分为高需求、中需求和低需求三种状态。零售商可以采取三种行动：大量补货、适量补货和不补货。

2.定义状态空间

   状态空间 S = {高需求状态，中需求状态，低需求状态}。

3.定义动作空间

   动作空间 A = {大量补货，适量补货，不补货}。

4.定义状态转移概率

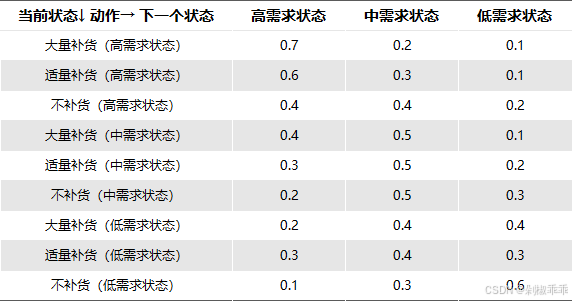
假设根据历史数据估计出以下状态转移概率：
   如果当前处于高需求状态：采取大量补货后，有 70% 的概率保持高需求状态，20% 的概率变为中需求状态，10% 的概率变为低需求状态。采取适量补货后，有 60% 的概率保持高需求状态，30% 的概率变为中需求状态，10% 的概率变为低需求状态。采取不补货后，有 40% 的概率保持高需求状态，40% 的概率变为中需求状态，20% 的概率变为低需求状态。
   如果当前处于中需求状态：采取大量补货后，有 40% 的概率变为高需求状态，50% 的概率保持中需求状态，10% 的概率变为低需求状态。
采取适量补货后，有 30% 的概率变为高需求状态，50% 的概率保持中需求状态，20% 的概率变为低需求状态。采取不补货后，有 20% 的概率变为高需求状态，50% 的概率保持中需求状态，30% 的概率变为低需求状态。
   如果当前处于低需求状态：采取大量补货后，有 20% 的概率变为高需求状态，40% 的概率变为中需求状态，40% 的概率保持低需求状态。采取适量补货后，有 30% 的概率变为高需求状态，40% 的概率变为中需求状态，30% 的概率保持低需求状态。采取不补货后，有 10% 的概率变为高需求状态，30% 的概率变为中需求状态，60% 的概率保持低需求状态。
用矩阵形式表示状态转移概率 P_ss’^a 如下：

5.定义奖励函数

奖励函数 R (s, a, s’) 表示在状态 s 采取动作 a 转移到状态 s’ 所获得的奖励值，这里奖励值以利润来衡量。假设：
   如果当前处于高需求状态：采取大量补货，每卖出一部手机获得利润 100 元，但如果有剩余库存，每部手机存储成本为 10 元。采取适量补货，每卖出一部手机获得利润 90 元，剩余库存存储成本为 8 元。采取不补货，每卖出一部手机获得利润 80 元，但可能因缺货损失一些潜在利润。
   如果当前处于中需求状态：采取大量补货，每卖出一部手机获得利润 80 元，剩余库存存储成本为 12 元。采取适量补货，每卖出一部手机获得利润 70 元，剩余库存存储成本为 10 元。采取不补货，每卖出一部手机获得利润 60 元，但可能因缺货损失一些潜在利润。
   如果当前处于低需求状态：采取大量补货，每卖出一部手机获得利润 60 元，剩余库存存储成本为 15 元。采取适量补货，每卖出一部手机获得利润 50 元，剩余库存存储成本为 12 元。
采取不补货，每卖出一部手机获得利润 40 元，但可能因缺货损失一些潜在利润。
用矩阵形式表示奖励函数如下：

6.定义折扣因子

设定折扣因子 γ = 0.9，表示未来奖励在当前决策中的重要性权重。

7.求解最优策略

首先计算每个状态的价值函数 V (s)，通过不断迭代贝尔曼方程：
V (s) = max_a∈A ∑_s’∈S P_ss’^a [R (s, a, s’) + γV (s’)]
假设初始时每个状态的价值函数都为 0，经过多次迭代后，得到以下近似的价值函数：
V (高需求状态) ≈ 某个具体数值   V (中需求状态) ≈ 某个具体数值
V (低需求状态) ≈ 某个具体数值
然后根据价值函数确定最优策略：
   在高需求状态时，计算采取不同动作后的期望收益，选择期望收益最高的动作作为最优动作。
在中需求状态和低需求状态时，同样进行类似计算，确定最优动作。

8.求解决策过程

   假设当前处于中需求状态，根据上述最优策略确定采取的动作（比如适量补货）。然后根据状态转移概率，系统可能转移到高需求状态、中需求状态或低需求状态中的一种，并获得相应的奖励。接着，根据新的状态和最优策略进行下一轮决策。

五、代码实现

import numpy as np

# 状态空间
states = ['高需求状态', '中需求状态', '低需求状态']

# 动作空间
actions = ['大量补货', '适量补货', '不补货']

# 状态转移概率矩阵
transition_probabilities = np.array([
    [0.7, 0.2, 0.1],
    [0.6, 0.3, 0.1],
    [0.4, 0.4, 0.2],
    [0.4, 0.5, 0.1],
    [0.3, 0.5, 0.2],
    [0.2, 0.5, 0.3],
    [0.2, 0.4, 0.4],
    [0.3, 0.4, 0.3],
    [0.1, 0.3, 0.6]
]).reshape(3, 3, 3)

# 奖励函数（假设示例值，实际需根据具体业务计算）
def reward_function(state, action, next_state):
    if state == '高需求状态':
        if action == '大量补货':
            return 100 if next_state == '高需求状态' else -10
        elif action == '适量补货':
            return 90 if next_state == '高需求状态' else -8
        else:
            return 80 if next_state == '高需求状态' else -5
    elif state == '中需求状态':
        if action == '大量补货':
            return 80 if next_state == '高需求状态' else -12
        elif action == '适量补货':
            return 70 if next_state == '高需求状态' else -10
        else:
            return 60 if next_state == '高需求状态' else -7
    else:
        if action == '大量补货':
            return 60 if next_state == '高需求状态' else -15
        elif action == '适量补货':
            return 50 if next_state == '高需求状态' else -12
        else:
            return 40 if next_state == '高需求状态' else -10

# 折扣因子
gamma = 0.9

# 初始化价值函数
values = np.zeros(len(states))

# 迭代更新价值函数
for _ in range(100):
    new_values = np.zeros(len(states))
    for s in range(len(states)):
        max_value = float('-inf')
        for a in range(len(actions)):
            value = 0
            for s_next in range(len(states)):
                value += transition_probabilities[s][a][s_next] * (reward_function(states[s], actions[a], states[s_next]) + gamma * values[s_next])
            max_value = max(max_value, value)
        new_values[s] = max_value
    values = new_values

# 根据价值函数确定最优策略
optimal_policy = [None] * len(states)
for s in range(len(states)):
    max_value = float('-inf')
    best_action = None
    for a in range(len(actions)):
        value = 0
        for s_next in range(len(states)):
            value += transition_probabilities[s][a][s_next] * (reward_function(states[s], actions[a], states[s_next]) + gamma * values[s_next])
        if value > max_value:
            max_value = value
            best_action = actions[a]
    optimal_policy[s] = best_action

print("价值函数：", values)
print("最优策略：", optimal_policy)

总结

马尔科夫决策模型通过考虑各种因素的影响，可以为在不确定环境下的决策提供了一种有效的方法，帮助决策者找到最优策略，以在长期运行中获得最大的收益或达到其他目标。