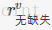【机器学习】决策树算法的基本原理

　　参考周志华老师的《机器学习》一书，对决策树算法进行总结。
　　决策树(Decision Tree)是在已知各种情况发生概率的基础上，通过构建决策树来求取净现值期望值大于等于0的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的图解法。
　　决策树算法是一种有监督学习算法，代表的是对象属性和属性值之间的映射关系。树中的每个结点表示某个对象。分叉路径代表可能的属性值。每个叶子结点为从根结点到该叶子结点所经历的路径所表示的对象的值。常用的决策树算法有ID3，C4.5，CART，随机森林等。

１.构建决策树的基本步骤：

(1)将数据集D看做一个结点
(2)遍历每个变量并计算一种划分方式，找到最好的划分点（属性）
(3)划分成结点D1和D2
(4)对D1和D2执行第(2)(3)步，直到满足停止生长条件。
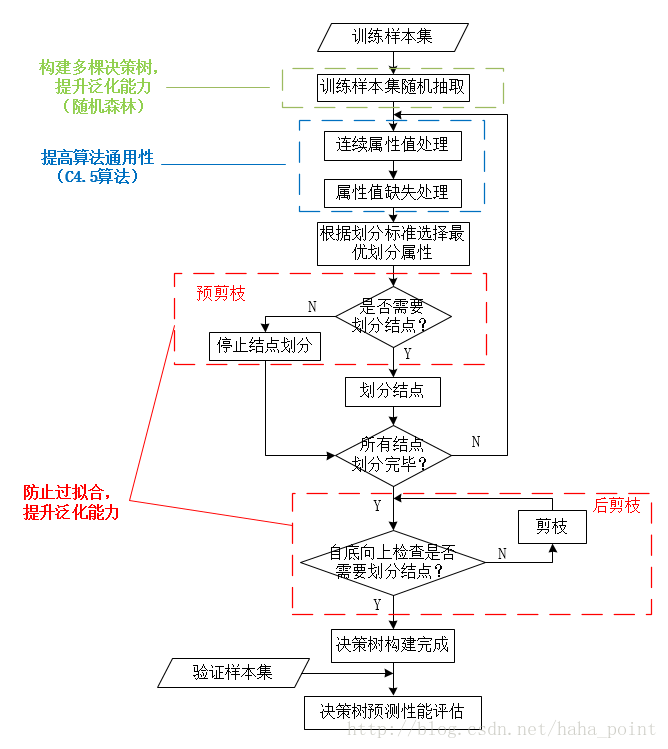
下图为决策树构建的流程图。注意，虚线框标注部分不是决策树构建必备步骤，有些是最基本的决策树算法的改进和扩展。
决策树构建流程图

２.结点划分标准

决策树根据信息纯度来构建，信息增益、信息增益率、Gini不纯度等经常被用来度量信息纯度，进行决策树构建。

ID3算法(1975年被提出)以“信息熵”为核心，计算每个属性的信息增益Gains(X,Y)，计算方法见公式(1)(2)。结点划分标准是选取信息增益最高的属性作为划分属性。ID3算法只能处理离散属性，并且类别值较多的输入变量比类别值少的输入变量更有机会成为当前最佳划分点。

G a i n s (X, Y) = E n t (X) - E n t (X | Y) = E n t (X) - \sum i = 0 v | D v | | D | E n t (D v) (1)

$Gains(X,Y)= Ent(X)-Ent(X|Y)= Ent(X)-\sum_{i=0}^v \frac{|D^v|}{|D|}Ent(D^v)\ (1)$

E n t (X) = - \sum i = 0 v p i log 2 p i (2)

$Ent(X)=-\sum_{i=0}^v p_{i}\log_{2}p_{i}\ (2)$ 其中，v是属性a的属性值取值个数。pi为第i类标签出现的概率。

C4.5算法使用信息增益率(公式(3))来选择属性，存在取值数目较少属性的偏好，因此，采用一个启发式搜索方法，先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择信息增益率最高的属性作为划分属性。基于这些改进，C4.5算法克服了ID3算法使用信息增益选择属性时偏向选择取值多的属性的不足。但信息增益率

G a i n s R (D) = G a i n s ( X , Y ) E n t ( Y ) (3)

$GainsR(D)= \frac{Gains(X,Y)}{Ent(Y)}\ (3)$

CART算法生成的决策树为结构简单的二叉树，每次对样本集的划分都计算Gini系数，Gini系数越小则划分越合理。Gini系数又称基尼不纯度，表示一个随机选中的样本在在子集中被分错的可能性。当一个结点中所有样本都属于一个类别时，Gini系数为0.

G i n i (D) = \sum i = 0 n P (i) (1 - P (i)) = \sum i = 0 n P (i) 2 - \sum i = 0 n P (i) 2 = 1 - \sum i = 0 n P (i) 2 (4)

$Gini(D)= \sum_{i=0}^n P(i)(1-P(i))= \sum_{i=0}^n P(i)^2- \sum_{i=0}^n P(i)^2=1- \sum_{i=0}^n P(i)^2\ (4)$

3.停止分裂,防止过拟合

　　过拟合是指直接生成的完全决策树，对训练样本的特征描述得“过于精确”，无法实现对新样本的合理分析。过拟合的决策树失去了一般的代表性，无法对新数据进行分类或预测。
　　针对过拟合，解决方法有:
　　(1)最小叶子结点限制、最大决策树深度限制。即当前结点中的记录数低于一个最小阈值，则停止分割，采取多数表决法决定叶结点的分类；当决策树结点划分次数大于最大深度时，停止决策树生长。
　　(2)对树进行剪枝。通过判断结点划分前后决策树泛化能力的变化，在完全分割训练样本前停止决策树生长(预剪枝)、决策树完全生长之后按照特定标准去掉某些子树(后剪枝)。一般情况下，后剪枝决策树的欠拟合风险小，泛化性能优于预剪枝决策树。但后剪枝是在完全决策树生成之后进行，自底向上对所有非叶子结点进行逐一判断，训练开销比预剪枝、未剪枝决策树大。

4.连续与缺失值处理

　　连续属性值的处理以C4.5算法为例进行介绍。C4.5算法除了改进信息增益对取值多的属性的偏好，还通过二分法实现了对连续属性值的处理。根据样本属性值计算属性候选划分点Ta，选取信息增益最大的划分点。

T a = {a i + a i + 1 2, 1 \leq i \leq n - 1} (5)

$Ta=\{{ \frac{a_i+a_{i+1}}{2}},1\le{i}\le{n-1}\}\ (5)$

　　通常离散属性在决策树构建过程中仅使用一次。与离散属性不同的是，当前结点划分属性为连续属性时，该属性可作为其后代结点的划分属性。也就是说，在父结点上使用属性A>123划分结点后，子结点仍可采用属性A>155进行结点划分。
　　对于缺失值的处理，主要通过计算各属性的取值在无缺失样本、有缺失样本中的概率，按照概率对信息增益、Gini不纯度计算进行加权即可。

G a i n s (D, a) = ρ \times G a i n (D 无 缺 失, a) = ρ \times (E n t (D 无 缺 失) - \sum i = 0 v r v 无 缺 失 E n t (D v 无 缺 失)) (6)

$Gains(D,a)=ρ×Gain(D_{无缺失},a)=ρ×(Ent(D_{无缺失})-\sum_{i=0}^v r_{无缺失}^v Ent(D_{无缺失}^v))\ (6)$

其中，ρ为无缺失样本所占比例。公式6参数表示无缺失样本中属性a为av的样本所占比例。