机器学习算法-线性回归
一. 理论基础
1.1 凸函数
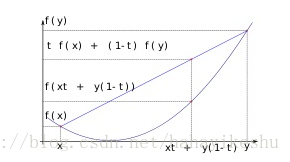
某个向量空间的凸子集(区间)上的实值函数,如果在其定义域上的任意两点 ,有 f(tx + (1-t)y) <= tf(x) + (1-t)f(y),则称其为该区间上的凸函数;
更直观的理解:
1.2 线性
线性不等于直线
线性函数的定义是:一阶(或更低阶)多项式,或零多项式。
当线性函数只有一个自变量时,y = f(x);
但如果有多个独立自变量,表示为:
f ( x 1 , x 2 , . . . . . . ) = a + b 1 x 1 + . . . . . . . . + b k x k f(x_1,x_2,......) = a+b_1x_1+........+ b_kx_k f(x1,x2,......)=a+b1x1+........+bkxk
总结: 特征是一维的,线性模型在二维空间构成一条直线;特征是二维的,线性模型在三维空间中构成一个平面;若特征是三维的,则最终模型在四维空间中构成一个体;以此类推……
1.3 极大似然估计
极大似然估计:从样本中随机抽取n个样本,而模型的参数估计量使得抽取的这n个样本的观测值的概率最大。最大似然估计是一个统计方法,它用来求一个样本集的概率密度函数的参数。
二. 线性回归模型(目标函数)
2.1 线性回归定义
利用线性函数对一个或多个自变量 (x 或 ( x 1 , x 2 , . . . . . . . , x k x_1,x_2,.......,x_k x1,x2,.......,xk))和因变量(y)之间的关系进行拟合的模型
2.2 线性回归模型
一般线性模型表示:
y ^ = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . . . . θ n x n \hat{y} = θ_0+θ_1x_1+\theta_2x_2+......\theta_nx_n y^=θ0+θ1x1+θ2x2+......