优化器：对参数进行调整，降低误差减小损失
torch.optimizer
parameters(模型参数)，lr(float)–>(学习速率)

代码：

import torch
import torchvision.datasets
from torch import nn
from torch.nn import Sequential, Conv2d, MaxPool2d, Flatten, Linear, CrossEntropyLoss
from torch.utils.data import DataLoader

# 加载数据集，转换成tensor类型
dataset = torchvision.datasets.CIFAR10(root="./dataset_ts",train=False, download=True,
                                       transform=torchvision.transforms.ToTensor())
dataloader = DataLoader(dataset, batch_size=1)

# 创建网络
class Tui(nn.Module):
    def __init__(self):
        super(Tui, self).__init__()
        self.model1 = Sequential(
            Conv2d(3, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 32, 5, padding=2),
            MaxPool2d(2),
            Conv2d(32, 64, 5, padding=2),
            MaxPool2d(2),
            Flatten(),
            Linear(1024, 64),
            Linear(64, 10)
        )

    def forward(self, x):
        x = self.model1(x)
        return x

#定义计算loss
loss = CrossEntropyLoss()

tui = Tui()
# 设置优化器
optim = torch.optim.SGD(tui.parameters(), lr=0.01)

for epoch in range(20):
    running_loss = 0.0
    for data in dataloader:
        imgs, targets = data
        outputs = tui(imgs)
        result_loss = loss(outputs, targets)#计算数据集经过神经网络后的输出和真实数据输出之间的误差
        optim.zero_grad()# 梯度清零————要把网络模型当中每一个 调节 参数梯度 调为0，参数清零
        result_loss.backward()# 反向传播求解梯度————调用存损失函数的反向传播，求出每个节点的梯度，
        optim.step()#   更新权重参数————调用优化器，对每个参数进行调优，循环
        running_loss = running_loss + result_loss#对整体损失的求和

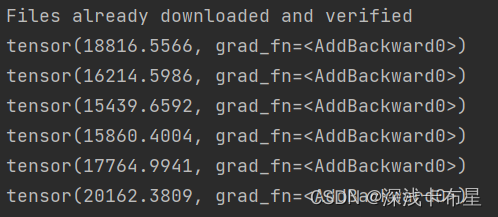
    print(running_loss)

运行结果：

总得来说，这三个函数的作用是：

先将梯度值归零，：optimizer.zero_grad()；
然后反向传播计算得到每个参数的梯度值：loss.backward()；
最后通过梯度下降执行一步参数更新：optimizer.step()；
由于pytorch的动态计算图，当我们使用loss.backward()和opimizer.step()进行梯度下降更新参数的时候，梯度并不会自动清零。并且这两个操作是独立操作。

基于以上几点，正好说明了pytorch的一个特点是每一步都是独立功能的操作，因此也就有需要梯度清零的说法，如若不显示的进行optimizer.zero_grad()这一步操作，backward()的时候就会累加梯度，也就有了梯度累加这种trick。

参考：
小土堆-优化器
https://blog.csdn.net/Crystalxxtt/article/details/124928155
https://blog.csdn.net/u013250861/article/details/120572718