文章目录
提示:以下是本篇文章正文内容,下面案例可供参考,以下纯属学习笔记。其中借助到了许多资料。书籍。
前序r d p q
除了在分布函数名前面加’r’表示生成随机数外,还可以加“p,q,d”
r- :表示生成相应分布的随机数
d- :生成相应分布的密度函数
p- :生成相应分布的累积概率密度函数
q- :生成相应分布的分位数函数(累积概率密度函数的逆函数)
例如:
dnorm: 生成正态分布密度函数
pnorm:生成正态分布累积概率密度函数
qnorm: 生成正态分布分位数函数
一、一元随机数的产生
1.均匀分布随机数runif
语法结构:runif(n,min=0,max=1)
runif(3,1,3)
省略参数min和max,默认在[0,1]上生成均匀分布随机数。
runif()默认每次生成的随机数不同,但有多种生成随机数的方法
当我们要求每次生成的随机数相同时,可以使用**set.seed()**设定随机数种子,其参数取整数,代表播的第几颗种子,后面在该种子下产生随机数。
(示例):
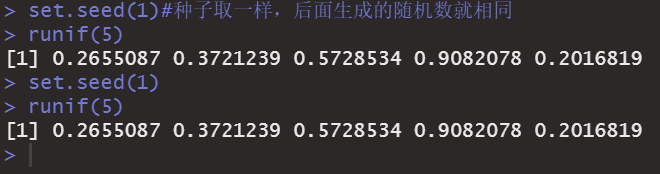
set.seed(1)#种子取一样,后面生成的随机数就相同
runif(5)
set.seed(1)
runif(5)
2.正态分布随机数的产生rnorm
涉及两个参数:位置参数mu(均值)、尺度参数sigma(标准差)生成正态分布随机数的函数是rnorm(),语法结构为:
rnorm(n,mean = ,sd = )
rnorm(5,10,5) #产生 5 个均值为 10 ,标准差为 5 的正态分布随机数
产生1000个正态分布随机数,做它们的概率直方图hist,再添加正态分布的密度函数线。
hist()表示画直方图,用法格式:
hist(v,main,xlab,xlim,ylim,breaks,col,border)
v 是包含直方图中使用数据的向量
main 直方图的标题
col 设置条的颜色
border 设置每个条的边框颜色
xlab 描述x轴(y轴是密度)
xlim 指定x轴上的值范围
ylim 指定y轴上的值范围
breaks设置条的宽度
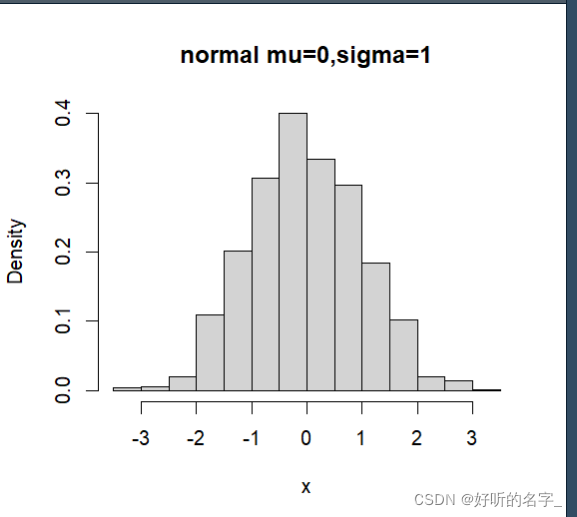
x=rnorm(1000)
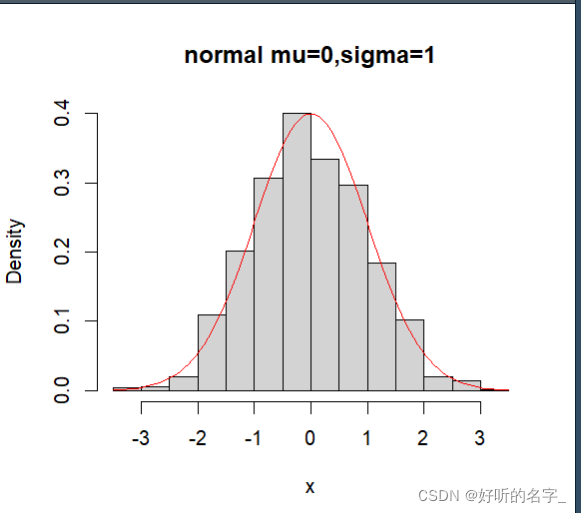
hist(x,prob=T,main="normal mu=0,sigma=1")
curve(dnorm(x),add=T,col=“red”)#添加正态分布密度函数线
add为逻辑值,add=T表示添加到一个已经存在的绘图中,
如果add=NA 则开始一个新的绘图
如果没有打开图形设备,则视为FALSE。
curve(dnorm(x),add=T,col="red")
3.指数分布随机数产生rexp
如果x服从指数分布,记为x~exp(λ),其中λ等于x的均值的倒数。
产生指数分布随机数的函数为:rexp(),
用法格式为rexp(n,lamda=1/mean),n为生成随机数的个数。
示例:
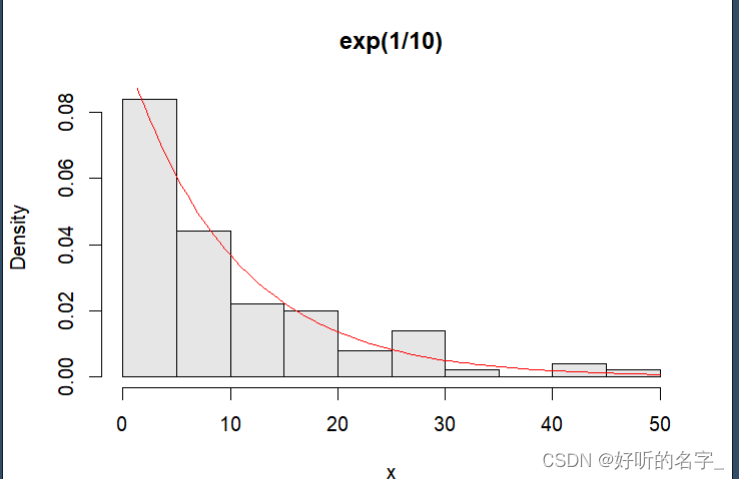
x=rexp(100,1/10) # 生成 100 个均值为 10 的指数分布随机数
hist(x,prob=T,col=gray(0.9),main="exp(1/10)") #gray表示灰色里面参数表示灰度
x
curve(dexp(x,1/10),add=T,col="red") #添加指数分布密度函数线(模拟指数分布曲线图)
rexp()和逆变换法比较
Nsim=10^4
U=runif(Nsim)
U
X=-log(U)
Y=rexp(Nsim)
par(mfrow=c(1,2)) #表示在1个界面画2个图
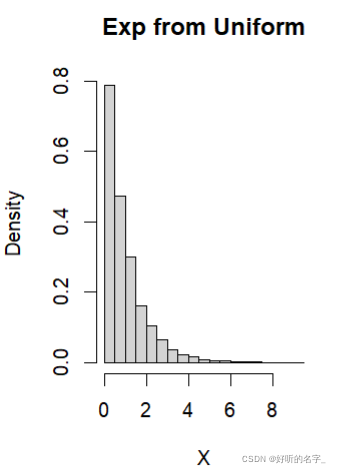
hist(X,freq=F,main="Exp from Uniform")
画X的直方图
freq为逻辑值,如果为TRUE表示直方图图形是频率的表示,即结果的计数成分
如果是FALSE,则绘制概率密度,即成分为密度(直方图的总面积为1)
curve(dexp(x,1),add=T,col="red")
#在直方图上添加密度函数曲线
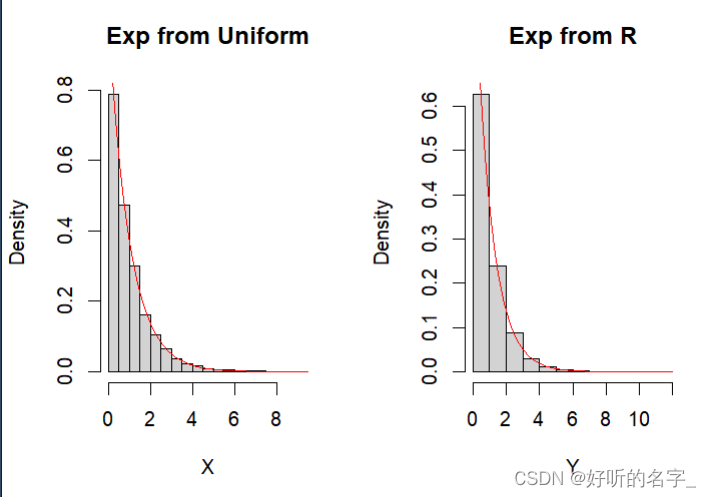
hist(Y,freq=F,main="Exp from R")
# 画Y的直方图
curve(dexp(x,1),add=T,col="red")
#在直方图上添加密度函数曲线
由以上两个直方图可以看出,这两者生成的随机数和指数分布X~Exp(1)都很接近.
4.二项分布随机数的产生rbinom
二项分布是指n次独立重复贝努力试验成功次数的分布。
每次贝努力试验的结果只有 成功和失败 两种,记成功的概率为p
如果变量x服从二项分布,记为:x~B(n,p),n表示试验次数,p表示成功概率。
生成二项分布随机数的格式为:
rbinom(n,size,prob)
n表示生成的随机数数量
size表示进行贝努力试验的次数
prob表示一次贝努力试验成功的概率
size=1; p=0.5
rbinom(10,size,p) #这里实质为两点分布
二项分布是离散分布,但随着试验次数n的增大,二项分布越接近于正态分布。
par(mfrow=c(2,2))#将4个图按照行排成2行2列
p=0.25
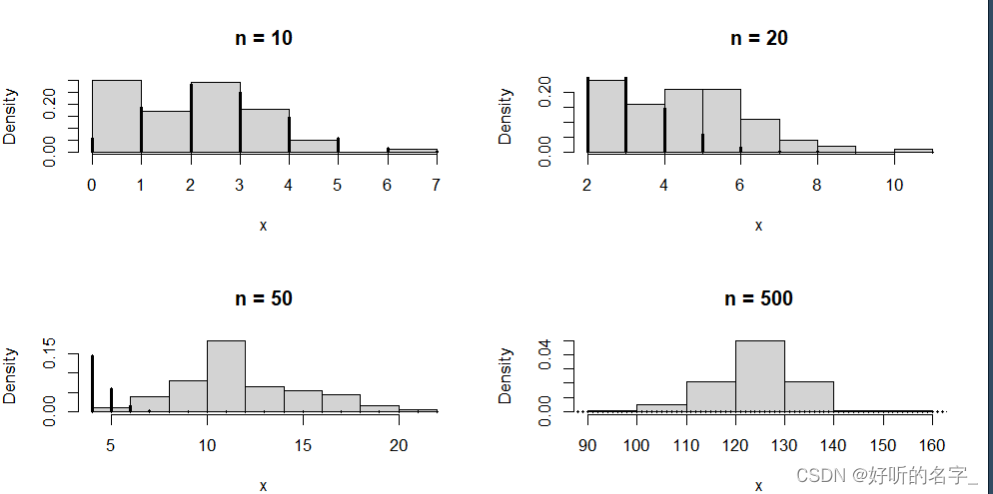
for( n in c(10,20,50,500))
{ x=rbinom(100,n,p)
hist(x,prob=T,main=paste("n =",n))#paste 拼接
xvals=0:n
points(xvals,dbinom(xvals,size,p),type="h",lwd=3)#在指定坐标上绘制一连串的点
}
可以发现随着试验次数n的增加,二项分布越来越接近正态分布。
除了前面介绍的几种分布的随机数外, 还可以生成Poisson分布、t分布和F分布等多种分布的随机数,只要在相应分布名前面加’r’就可以了。
例如,泊松分布(poisson)随机数的产生:
泊松分布也是离散分布
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布
密度函数为:p(X=k)=((λ^k)*(exp(-λ)))/(k!)(k=0,1,…)
记为:X~P(λ), 其中λ=E(X)=V(X)
产生泊松分布随机数的函数为: rpois(n,λ)
rpois(10,7)
求标准正态分布P(x <= 2 )的累积概率
pnorm(2)
## 已知标准正态分布累积概率为P(x<=a)=0.95,求对应的分位数a.
qnorm(0.95)
## 服从正态分布x~N(1,2),求p(x<=a)=0.05,求a
qnorm(0.05,1,sqrt(2))
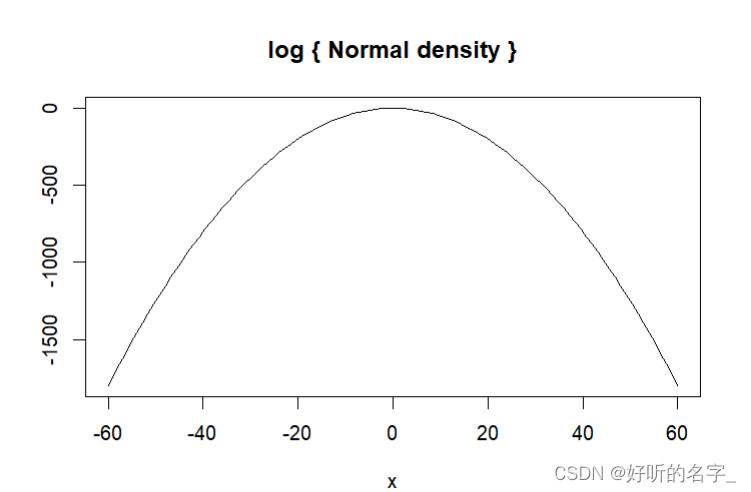
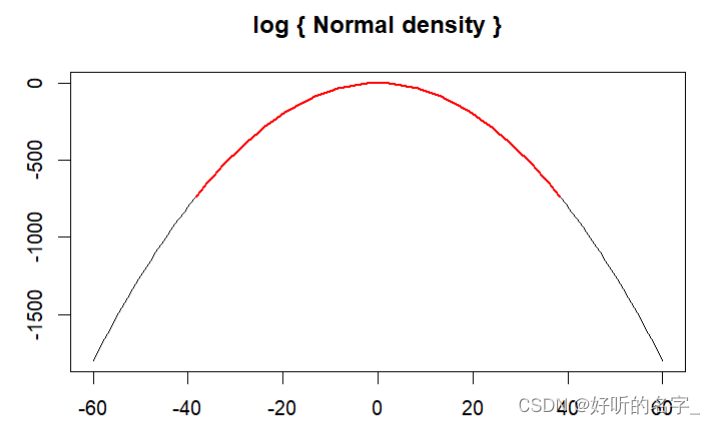
plot(function(x) dnorm(x, log = TRUE), ylab="",-60, 60,
main = "log { Normal density }")
正态分布密度函数dnorm()中的log为逻辑值,如果为TURE,则概率p以log§给出。
curve(log(dnorm(x)), add = TRUE, col = "red", lwd = 2)
t分布
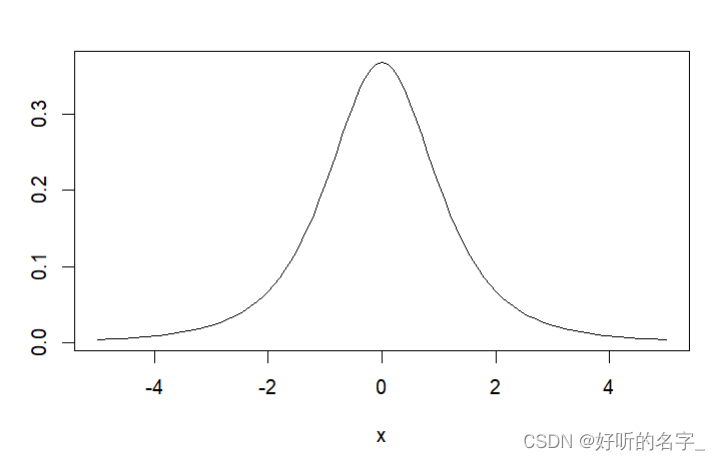
plot(function(x) dt(x,3),ylab="",-5,5)
#dt(x,3)表示服从自由度为3的t分布密度函数
F分布
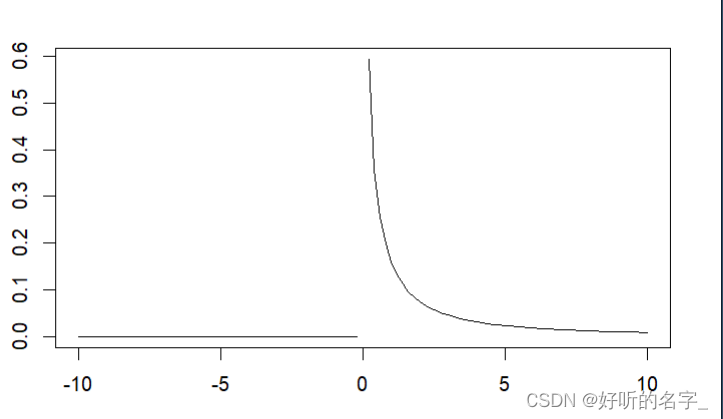
plot(function(x) df(x,1,1),ylab="",-10,10)
#绘制自由度为1,1的F分布密度函数曲线
二、多元随机数的产生mv,rm,pm
1.多元正态分布随机数
产生多元正态分布随机数的方法:
**方法一:**可以使用MASS包中的 mvrnorm()函数
用法格式:
mvrnorm(n = 1, mu, Sigma, tol = 1e-6, empirical = FALSE, EISPACK = FALSE)
n:生成的随机数个数
mu: 均值向量
Sigma: 协方差矩阵
tol: 容忍度(精度)
empirical:逻辑参数,取TRUE时,mu和Sigma取经验均值和协方差阵
**例:**如果需要产生均值都是0、协方差矩阵为
V=matrix(c(10,3,3,2),2,2)的二元正态分布随机数,
library(MASS)
Sigma <- matrix(c(10,3,3,2),2,2)
Sigma
x=mvrnorm(n=1000, rep(0, 2), Sigma)
x
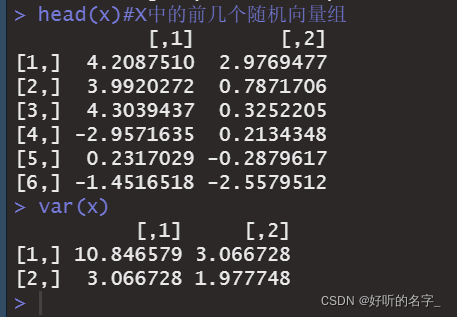
head(x)#X中的前几个随机向量组
var(x)
**方法二:**利mvtnorm包中的rmvnorm()函数, 格式如下:
n 为生成随机数的个数
mean 为均值向量
sigma 为协方差矩阵
method 提供了三种对sigma矩阵进行分解的方法:
特征根分解‘eign’(默认),奇异值分解‘sv’,以及cholesky分解‘chol’。
例:生成均值为(1,2),协方差阵为
V=matrix(c(10,3,3,2),2,2) 的二元正态分布随机数。
install.packages("mvtnorm")
library(mvtnorm)
sigma <- matrix(c(10,3,3,2), ncol=2)
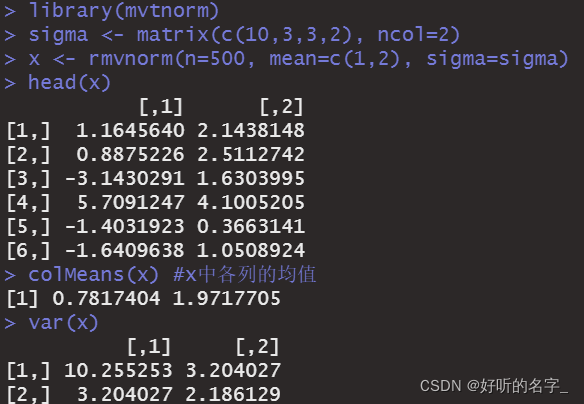
x <- rmvnorm(n=500, mean=c(1,2), sigma=sigma)
head(x)
colMeans(x) #x中各列的均值
var(x)
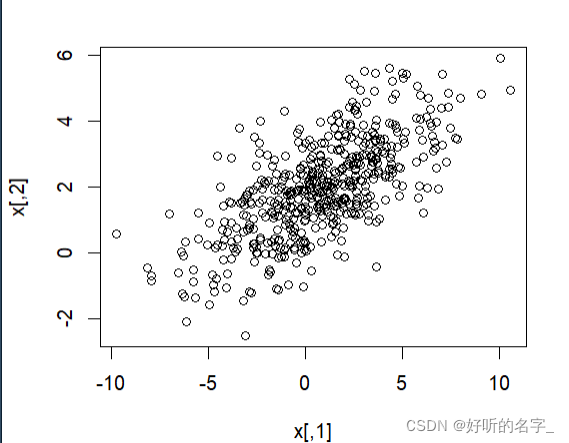
plot(x)# 绘制二元正态分布随机数X的散点图。
从散点图可知,两个正态分布随机数呈正相关关系。
可以从协方差阵里面算出相关系数。
设置图形参数:
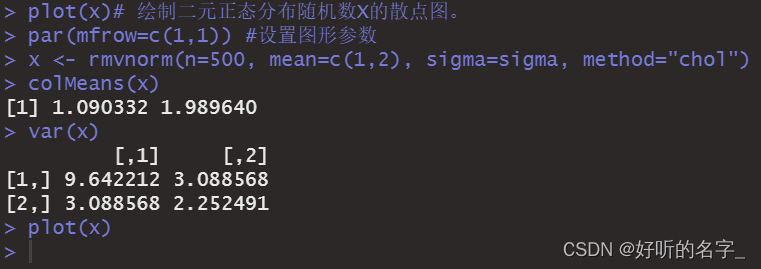
par(mfrow=c(1,1)) #设置图形参数
x <- rmvnorm(n=500, mean=c(1,2), sigma=sigma, method="chol")
colMeans(x)
var(x)
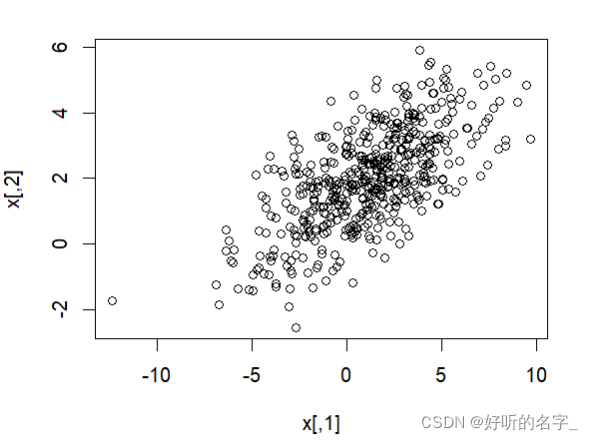
plot(x)
2.多元正态分布的累积概率、密度函数、分位数
与一元随机数类似,可以利用pmvnorm()计算累积概率
用法格式:
pmvnorm(lower=-Inf, upper=Inf, mean=rep(0, length(lower)),
corr=NULL, sigma=NULL)
lower 是求累积概率的下限,默认为负无穷
upper 是求累积概率的上限,默认为正无穷
mean 是多元正态分布的均值向量
corr 是多元正态分布的相关系数矩阵
sigma 是协方差矩阵
其中,相关系数corr和协方差矩阵sigma只要知道一个即可。
**例:**求
五元正态分布随机数的均值为0,相关系数矩阵为
c(1,0.5,0.5,0.5,0.5,
0.5,1,0.5,0.5,0.5,
0.5,0.5,1,0.5,0.5,
0.5,0.5,0.5,1,0.5,
0.5,0.5,0.5,0.5,1)
下限为(-1,-1,-1,-1,-1),上限为(3,3,3,3,3)的累积概率。dig单位矩阵
(mean <- rep(0, 5))#均值向量
(lower <- rep(-1, 5))#下限
(upper <- rep(3, 5))#上限
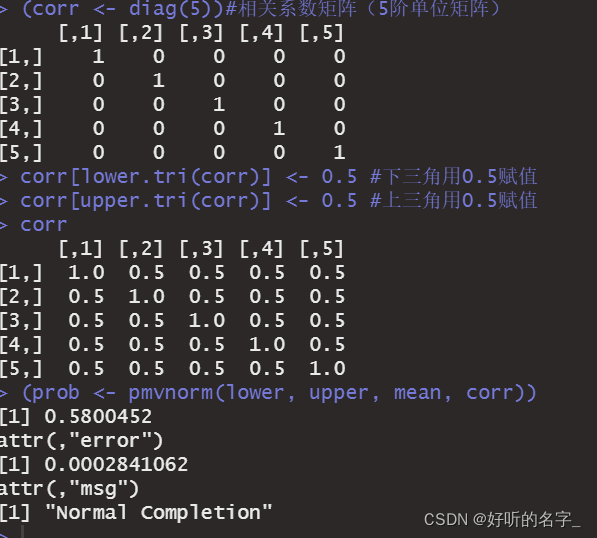
(corr <- diag(5))#相关系数矩阵(5阶单位矩阵)
corr[lower.tri(corr)] <- 0.5 #下三角用0.5赋值
corr[upper.tri(corr)] <- 0.5 #上三角用0.5赋值
corr
(prob <- pmvnorm(lower, upper, mean, corr))
误差为:0.00028
正常运行
**同理,**可以用dmvnorm()求多元正态分布的密度函数
用qmvnorm()求多元正态分布的分位数。
3.多元t分布随机数
多元t分布随机数,可以利用mvtnorm包中的rmvt()函数
用法:
rmvt(n, sigma = diag(2), df = 1)
n是需要生成的随机数个数
sigma 是事先给定的协方差矩阵
df 是t分布的自由度,默认为1.
library(mvtnorm)
x <- rmvt(n=100, sigma = diag(2), df = 3)
x
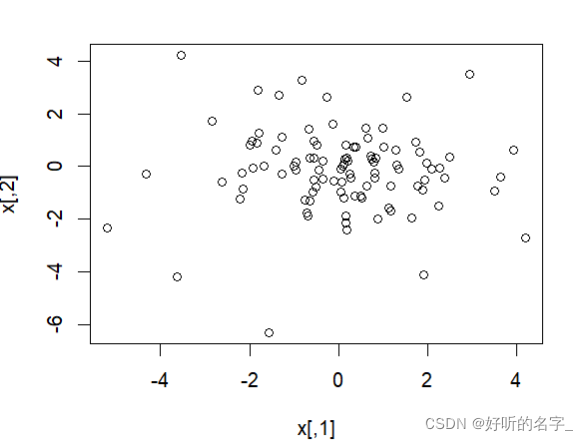
plot(x)#画二元t分布随机数x的散点图
sigma=diag(2)+1
sigma
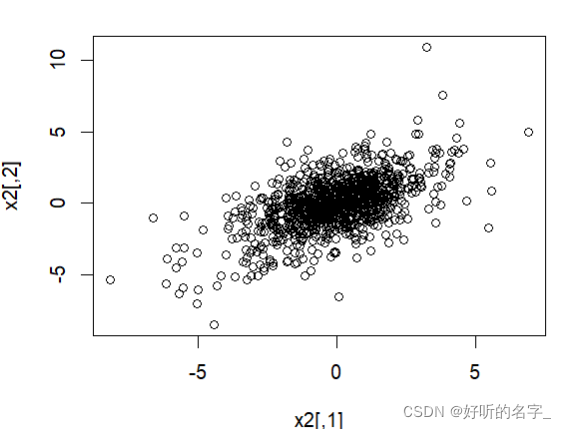
x2 <- rmvt(n=1000,df=5,sigma=sigma)
head(x2)
plot(x2)
三、随机抽样sample
1.放回与无放回抽样
利用R进行抽样很简单,运用sample()函数即可,语法结构如下:
sample(x, n, replace = FALSE, prob = NULL)
x表示总体向量(数值、字符、逻辑向量均可)
n表示样本容量
replace=F,表示无放回抽样(默认);replace=T,表示有放回抽样
prob,可以设置各个抽样单元不同的入样概率,进行不等概率抽样。
**例1:**利用R模拟抛一枚硬币,H表示正面,T表示背面,重复抛10次的情况。
**例2:**模拟抛一枚六面的骰子,重复抛10次。
**例3:**模拟从100个产品中无放回随机抽取10个。
**例4:**模拟:抛两颗六面的骰子,抛10次。
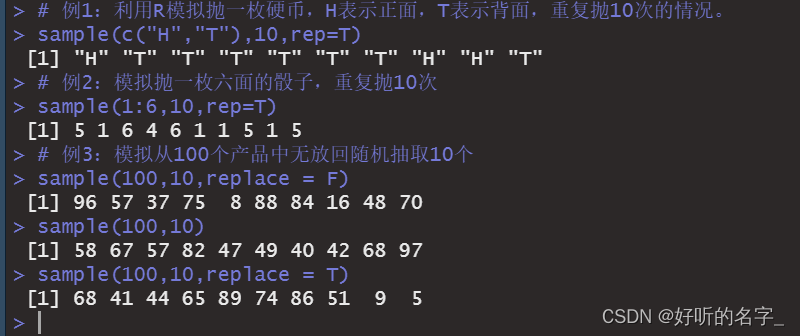
# 例1:利用R模拟抛一枚硬币,H表示正面,T表示背面,重复抛10次的情况。
sample(c("H","T"),10,rep=T)
# 例2:模拟抛一枚六面的骰子,重复抛10次
sample(1:6,10,rep=T)
# 例3:模拟从100个产品中无放回随机抽取10个
sample(100,10,replace = F)
sample(100,10)
sample(100,10,replace = T)#有放回
**例4:**模拟:抛两颗六面的骰子,抛10次
先给出抽样的总体:
(dice=as.vector(outer(1:6,1:6,paste)))
以上命令表示,抛两颗六面的骰子的可能结果。
outer(a,b,function)中,function为空时,表示a,b两个向量的外积,等价于a%o%b
outer(1:6,1:6,paste)中,function为paste,表示a中的第一个元素与b中的每一个元素分别组合,组成第一行;接着a中的第二个元素与b中的每个元素分别组合,组成第2行,这样直到a中的最后一个元素组合完毕。
outer(1:6,1:6,paste)的结果是一个矩阵形式,as.vector()表示强制将()里面的对象转换为向量形式。
sample(dice,10,replace=T)
2.重抽样
bootstrap重抽样,属于重复抽样方法。
基本思想:
在原始数据的范围内做有放回的再抽样,样本量仍为n,原始数据中每个观测单位每次
被抽中的概率相等,为1/n,所得的样本称为bootstrap样本。
R内置数据faithful中的"eruptions(喷发)"变量,用于记录火山喷发时间,属于不常见的分布。
下面对"eruptions(喷发)"变量数据进行bootstrap重抽样:
data(faithful)#读入数据
faithful
head(faithful)
attach(faithful)
sample(eruptions,10,rep=T) #从数据中抽一个样本量为10的子样本
Sample=sample(eruptions,272,rep=T) #从数据中抽一个样本量为272的子样本
Sample
par(mfrow=c(1,2))#设置作图窗口为1行2列
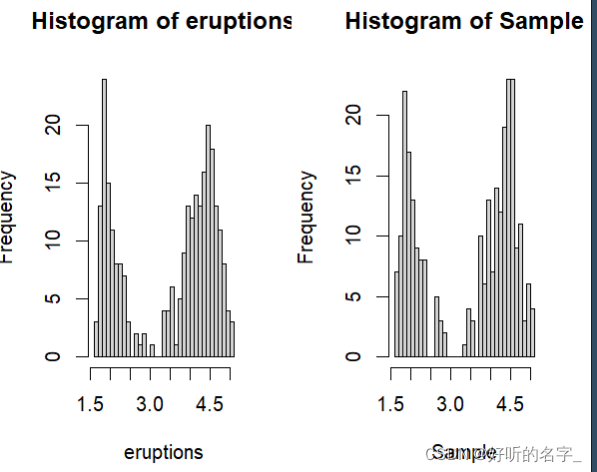
hist(eruptions,breaks=25)
hist(Sample,breaks=25);
# 从两个直方图可以看出,两个图形比较接近。
par(mfrow=c(1,1)) #设置作图窗口为一行一列
detach() #解除数据绑定
四、统计模拟
几种常见的模拟方法
1. 二项分布模拟中心极限定理
设x~B(n,p),则X的标准化变量 y=(Z-np)/((np(1-p))^(1/2))
当n趋于无穷大时,y的分布依概率收敛于标准正态分布。
下面利用统计模拟方法检验该定理的正确性。
首先生成二项分布随机数的标准化变量
n=10;p=0.25
x=rbinom(1,n,p) #生成1个服从参数为n,p的二项分布随机数
y=(x-n*p)/sqrt(n*p*(1-p)) #对x进行标准化
y
这只是一个随机数标准化后的结果,需要产生很多随机数并观察它们的分布情况。
比如产生1000个这样的随机数:
m =1000 # 模拟次数
n=100; p=0.25
b=rbinom(m,n,p) # 产生1000个随机数
x=(b-n*p)/sqrt(n*p*(1-p)) # 标准化
hist(x,prob=T,main=paste("n =",n))
curve(dnorm(x),add=T,col=2) # 添加正态曲线
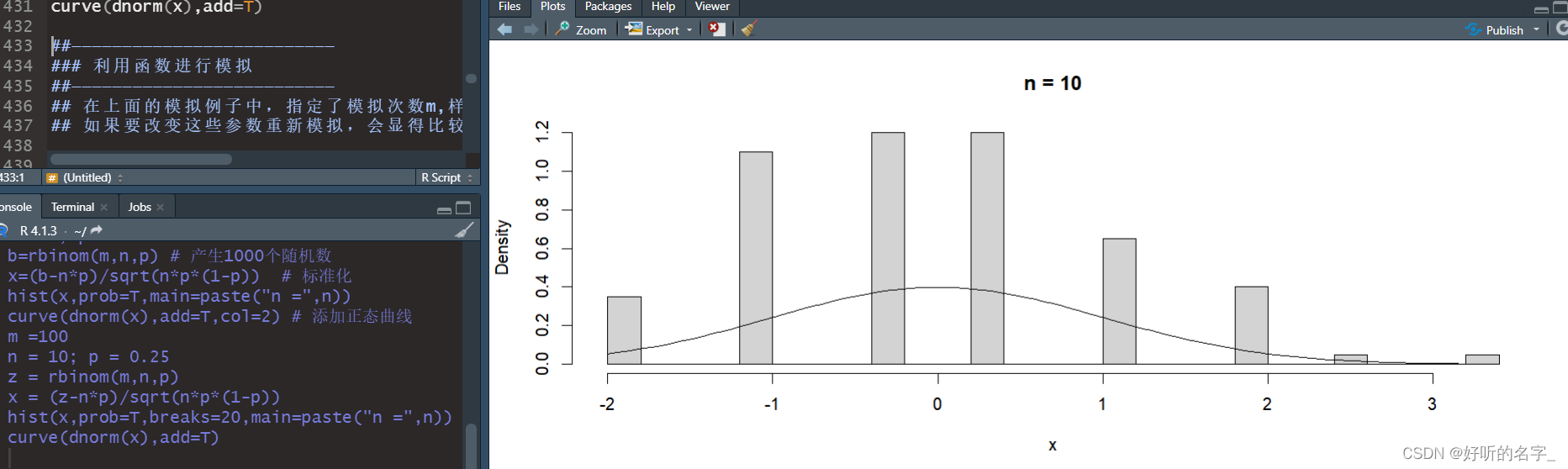
m =100
n = 10; p = 0.25
z = rbinom(m,n,p)
x = (z-n*p)/sqrt(n*p*(1-p))
hist(x,prob=T,breaks=20,main=paste("n =",n))
curve(dnorm(x),add=T)
2.利用函数进行模拟
在上面的模拟例子中,指定了模拟次数m,样本量n,概率p。
如果要改变这些参数重新模拟,会显得比较麻烦,可以考虑写成一个模拟函数进行模型。
sim.clt <- function (m=100,n=10,p=0.25)
{ z = rbinom(m,n,p)
x = (z-n*p)/sqrt(n*p*(1-p))
hist(x,prob=T,breaks=20,main=paste("n =",n,"p =",p))
curve(dnorm(x),-4,4,add=T,col=2)
}
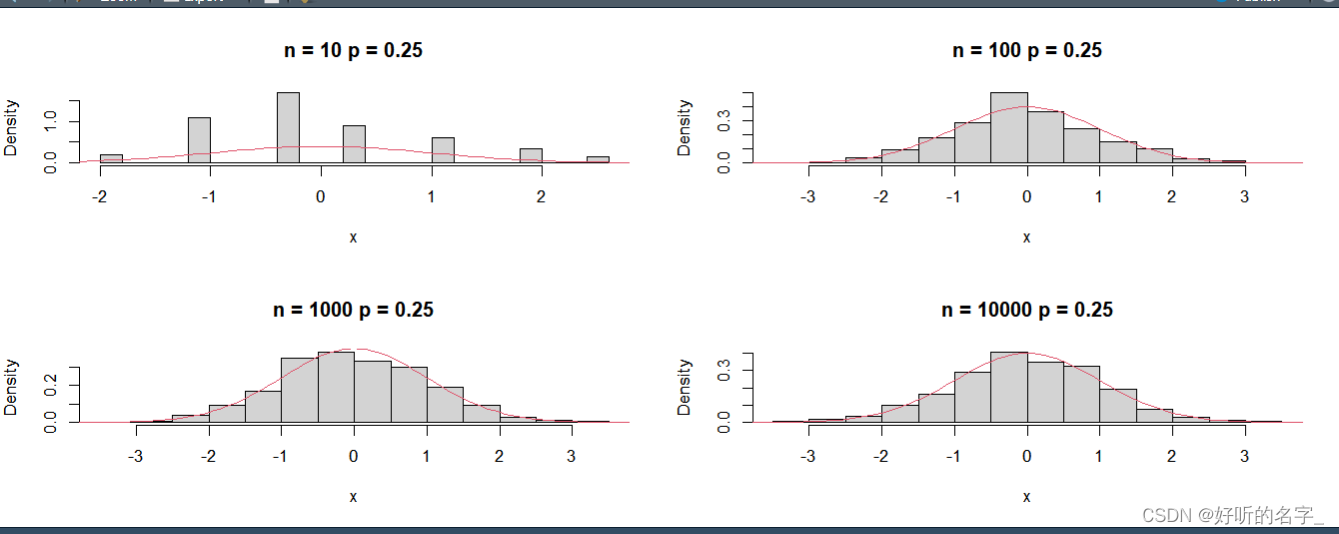
par(mfrow=c(2,2))
sim.clt() # 默认m=100,n=10,p=0.25
sim.clt(1000,100)
sim.clt(1000,1000)
sim.clt(1000,10000)
par(mfrow=c(1,1))
3.正态概率模拟
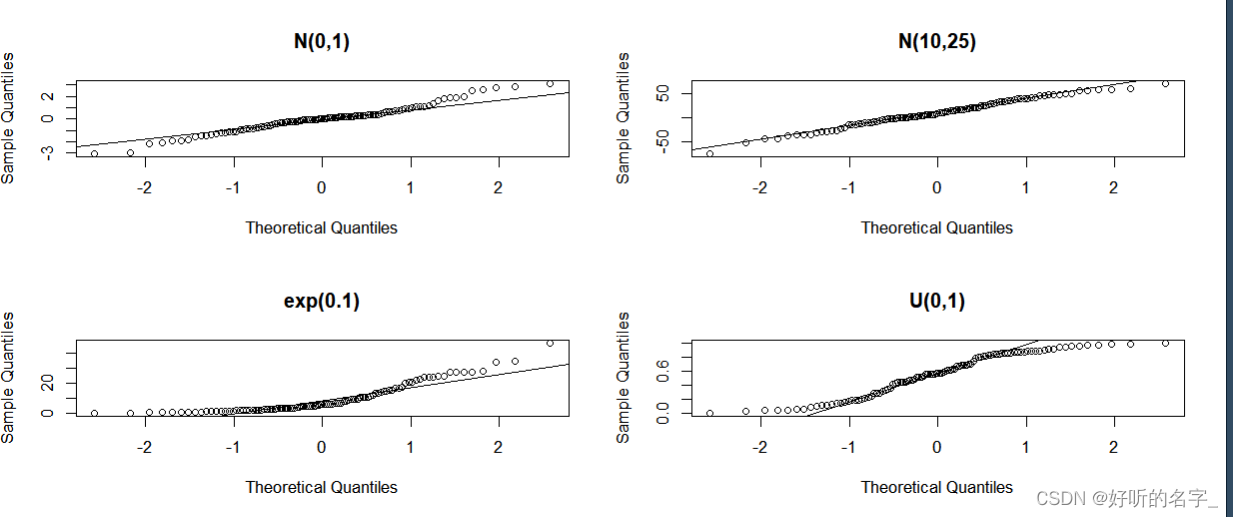
par(mfrow=c(2,2))
x=rnorm(100,0,1)
qqnorm(x,main="N(0,1)")
qqline(x)
x=rnorm(100,10,25);qqnorm(x,main="N(10,25)");qqline(x)
x=rexp(100,1/10);qqnorm(x,main="exp(0.1)");qqline(x)
x=runif(100,0,1);qqnorm(x,main="U(0,1)");qqline(x)
par(mfrow=c(1,1))
4.模拟函数的建立方法
sim.fun <- function (m,f,...)
{
sample <- 1:m
for (i in 1:m) {
sample[i] <- f(...)
}
sample
}
f <- function (n=10,p=0.5) {
S = rbinom(1,10,p)
(S- n*p)/sqrt(n*p*(1-p) )
}
x=sim.fun(1000,f(n=1000))
hist(x,prob=T)
f1=function(n=10) (mean(runif(n))-1/2)/(1/sqrt(12*n))
x=sim.fun(1000,f1(n=1000))
hist(x,prob=T,main="n=1000")
curve(dnorm(x),-4,4,add=T,col=2)
#lines(dnorm(x))
f <- function(n=100,mu=10) (mean(rexp(n,1/mu))-mu)/(mu/sqrt(n))
x=sim.fun(10,f)
f2 <- function(n=10,mu=0,sigma=1){
r=rnorm(n,mu,sigma)
(mean(r)-mu)/(sigma/sqrt(n))
}
x = sim.fun(1000,f2)
hist(x,breaks=10,prob=T)
x = sim.fun(1000,f,30,5,2)
hist(x,breaks=10,prob=T)
f <- function(n,mu=10)(mean(rexp(n,1/mu)-mu))/(mu/sqrt(n))
x=seq(-3,3,0.01)
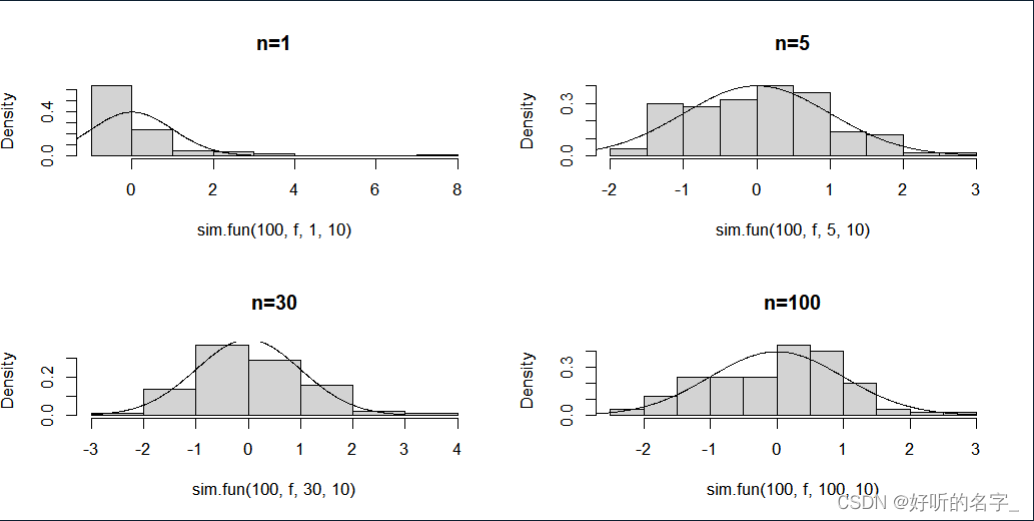
par(mfrow=c(2,2))
hist(sim.fun(100,f,1,10),prob=T,main="n=1")
points(x,dnorm(x,0,1),type="l")
hist(sim.fun(100,f,5,10),prob=T,main="n=5")
points(x,dnorm(x,0,1),type="l")
hist(sim.fun(100,f,30,10),prob=T,main="n=30")
points(x,dnorm(x,0,1),type="l")
hist(sim.fun(100,f,100,10),prob=T,main="n=100")
points(x,dnorm(x,0,1),type="l")
par(mfrow=c(1,1))
参考教材:《R数据分析方法与案例详解》