文章目录
1-3. 概念题
4. 如何限制空间
1.约束版本
对于线性回归问题,限定参数向量
w的大小,即||w||₂ ≤ c。这里c是一个预先设定的常数,用于限制w的长度。这个约束条件直接对参数向量的长度进行了限制,确保其不会过大或过小。
2.无约束版本min 1 2 N ∣ ∣ X w − y ∣ ∣ 2 2 + λ 2 ∣ ∣ w ∣ ∣ 2 2 \min\frac{1}{2N}||Xw - y||_2^2+\frac{\lambda}{2}||w||_2^2 min2N1∣∣Xw−y∣∣22+2λ∣∣w∣∣22
N是样本数量,X是输入数据矩阵,w是参数向量,y是目标值向量。这个目标函数由两部分组成:第一部分是均方误差项,表示模型对数据的拟合程度;第二部分是正则化项,通过惩罚参数向量w的长度来防止过拟合。参数λ用于控制正则化的强度。
通过调整λ的值,可以在拟合数据和限制参数大小之间进行权衡。当λ较大时,正则化项的作用更强,参数向量w会更趋向于零向量,从而防止过拟合;当λ较小时,正则化项的作用较弱,模型更注重拟合数据。例如,在实际应用中,可以通过交叉验证等方法来选择合适的
λ值,以获得最佳的模型性能。
5. 梯度下降的计算
6. 随机梯度下降
在随机梯度下降(Stochastic Gradient Descent,SGD)中,批大小(batch size)对训练过程有着重要的影响,具体如下:
一、批大小较小时的影响
- 随机梯度噪声大:
- 当批大小很小时,每次用于计算梯度的样本数量少。由于样本的随机性,每次计算得到的梯度与使用全量数据计算的真实梯度之间的偏差较大,这就导致了随机梯度的噪声非常大。
- 例如,在图像分类任务中,如果批大小为 1 或 2,那么每个小批次的样本可能具有很大的特殊性,计算出的梯度可能会在不同的方向上剧烈波动,使得模型难以稳定地朝着最优解方向前进。
- 不易收敛:
- 由于随机梯度的噪声大,模型在训练过程中会频繁地在不同方向上进行大幅度的参数更新,难以稳定地收敛到一个较好的解。
- 比如,在回归问题中,小批大小可能导致模型在训练过程中不断地在最优解附近振荡,无法准确地找到最小损失值对应的参数值。
- 此外,小批大小还可能使模型陷入局部最优解,因为在噪声较大的情况下,模型更容易被一些局部的、不稳定的梯度方向所引导。
二、批大小较大时的影响
- 运行速度慢:
- 当批大小较大时,每次参与梯度计算的样本数量多。这虽然可以使计算得到的梯度更接近真实梯度,减少随机梯度的噪声,但同时也会增加计算量和内存占用。
- 例如,在大规模数据集上,如果批大小设置得非常大,可能会导致每次迭代需要花费很长时间来计算梯度,从而使整个训练过程的运行速度变得非常慢。
- 特别是在硬件资源有限的情况下,如内存较小的设备,大的批大小可能会导致内存溢出等问题,进一步影响训练的效率。
- 可能陷入局部最优:
- 较大的批大小可能会使模型在训练过程中过于“平滑”地更新参数,缺乏对不同局部区域的探索能力。
- 这意味着模型可能更容易陷入局部最优解,而错过全局最优解。
- 例如,在复杂的神经网络训练中,大的批大小可能会使模型在某些局部最优解附近停留,而无法跳出该区域去寻找更好的解。
综上所述,在随机梯度下降中,选择合适的批大小非常重要。一般来说,需要根据数据集的大小、硬件资源以及模型的复杂度等因素来综合考虑,以平衡随机梯度的噪声和训练的效率,从而获得更好的训练效果。
7. Softmax计算
8. 岭回归思想
岭回归的基本思想如下:
一、问题背景
在传统的线性回归中,通常使用最小二乘法来求解模型参数,其目标是最小化损失函数 1 2 ∣ ∣ X w − y ∣ ∣ 2 2 \frac{1}{2}||Xw - y||_2^2 21∣∣Xw−y∣∣22,其中(X)是输入数据矩阵,(w)是模型参数向量,(y)是目标值向量。然而,在实际应用中,当数据特征较多或者存在相关性时,普通的线性回归容易出现过拟合的问题。
二、基本思想引入
为了解决过拟合问题,岭回归在普通线性回归的损失函数基础上引入了对参数向量(w)的约束。具体来说,岭回归希望同时限定 ∣ ∣ w ∣ ∣ 2 2 ||w||_2^2 ∣∣w∣∣22(即(w)的长度平方)的大小,要求(w)的长度满足 ∣ ∣ w ∣ ∣ 2 2 ≤ c ||w||_2^2\leq c ∣∣w∣∣22≤c,其中(c)是一个预先设定的常数。这样做的直觉是,通过限制参数向量的长度,可以有效地缩小解空间的大小。
三、作用及意义
- 解决过拟合:限制解空间的大小有助于防止模型过度拟合训练数据。当解空间被限制时,模型不能自由地适应训练数据中的噪声和细微变化,从而减少了过拟合的风险。例如,在高维数据中,可能存在许多特征之间的相关性,而普通线性回归可能会过度依赖某些特征,导致过拟合。岭回归通过限制参数向量的长度,使得模型在选择特征时更加谨慎,从而提高了模型的泛化能力。
- 稳定性提升:对参数向量的约束还可以使模型更加稳定。在数据存在噪声或不确定性的情况下,岭回归可以减少参数估计的方差,使得模型对不同的数据集具有更好的鲁棒性。例如,在实际应用中,数据的采集和测量可能存在误差,岭回归可以帮助模型在面对这些误差时更加稳定地进行预测。
总之,岭回归的基本思想是在普通线性回归的基础上,通过引入对参数向量长度的约束,来解决过拟合问题并提高模型的稳定性和泛化能力。
9. 套索回归基本思想
通过这样的约束,套索回归能够促使模型在众多特征中选择出最重要的一部分特征,将不重要的特征对应的参数设置为零,从而实现特征选择和提高模型的解释性,同时也有助于防止过拟合,提高模型的泛化能力。
10. Sigmoid函数
11. 岭回归范数
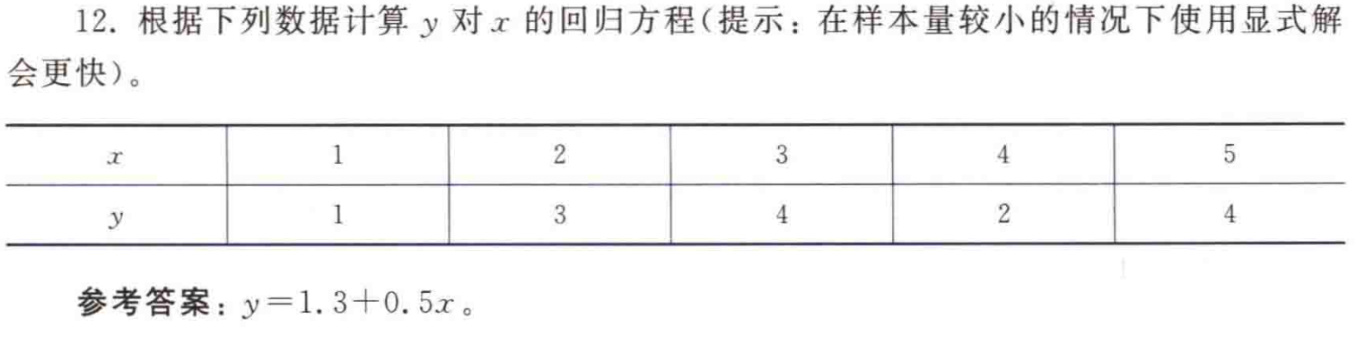
12. 计算回归方程
参考:《人工智能基础-姚期智》