一个数组的最大子数组和可能存在于三种情况中:

1. 该数组的左子数组中

2.该数组的右子数组中

3.可能横跨左右子数组

所以，我们可以将问题分解成一个个的子问题，其中情况1和2可用递归求解，而情况3则需要计算

s1=max{ } (1 <= i <= n/2), s2=max{ } （n/2+1 <= j <=n），其中情况3中s1必然包含了,

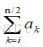
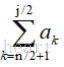
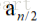
s2中必然包含了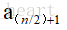，因为情况3跨越了左右子数组。s1 + s2为情况3的最大子数组。

代码(记录了最大数组和的范围)：

/*
 * 利用分治法求最大子数组问题
 */
public class TestOne {

	public static int leftFlag;	//负责记录最大子数组和的开始下标
	public static in