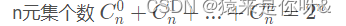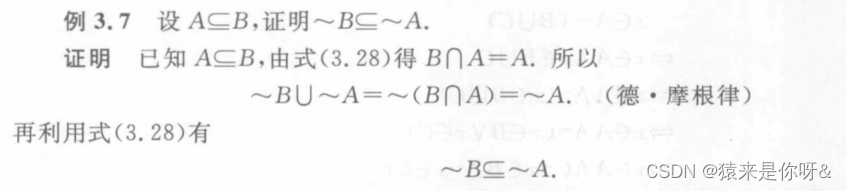本章知识点
1.集合:一些可确定的、可分辩的事物构成的整体
元素,集合中的特定的事物
N代表自然数集合(包括0),Z代表整数集合,Q代表有理数集合,R代表实数集合,C代表复数集合

2.子集合(子集):设A、B为集合,如果B中的每个元素都是A中的元素,则B是A的子集,称B被A包含,或A包含B 记 B⊆A
包含的符号化 B⊆A⇔∀x(x∈B→y∈A)
相等:设A、B为集合,如果A⊆B且B⊆A,则称A 与B相等,记作A=B.
记为A=B⇔A⊆B∩B⊆A
真子集:设A、B为集合,如果 BCA且B≠A,则称B是A的真子集,记作 B⊂A.不是真子集则为非子集或相等
空集:不含任何元素的集合,记作∅．
空符号化表示为∅={x|x≠x } .
空集是一切集合的子集,且空集是唯一的
∅:无元素
{∅}:含空集元素

3.n元集:含n个元素的集合
m元子集:n元集的含m个(m<=n)元素的子集

n元集的子集的总数是0元子集和1元子集…n元子集的总和
幂集:集合A的全体子集构成的集合,记为P(A)
符号化:P(A)={x|x⊆A}
P(A)={∅,{a},{b},{c},{a,b} ,{a,c },{b,c},{a,b,c}}.

注:求幂集时一定要有2^n个
全集:在一个具体问题中,如果涉及的集合都是某个集合的子集,则称这个集合为全集，记为E(或U)

4、集合的基本运算
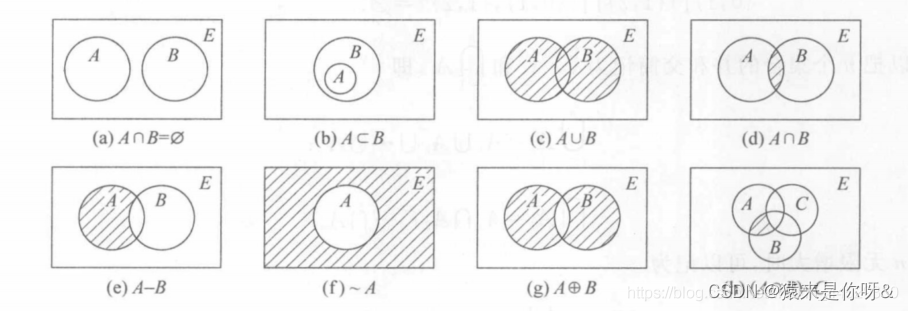
五种集合运算符:并(∪)交(∩)相对补(-)绝对补(~)对称差(⊕)
并集:A∪B={x|x∈A∨x∈B}
交集:A∩B={x|x∈A∧x∈B}
相对补集:A-B=A-AB={x|x∈A∧x∉B}
不交:两集合的交集为空集
n个集合的交集

绝对补集:设E为全集,A⊆E,则称A对E的相对补集为A的绝对补集,记作～A=E-A={x|x∈E∧x∉A}={x∉A}

对称差:去掉集合A和B所共有的再合并或者先求并集再去掉交集
记为A⊕B=A⊕B=(A-B)∪(B-A)=(A∪B)-(A∩B)
文氏图：

5.集合运算律:

例：

6.基数:集合A={1,2,…,n},含有n个元素,这个集合的基数是n,记为card A = n 表示集合中所含元素多少的量,也可记为|A|=n
|∅|=0
有穷集:设A为集合,若存在自然数n(0也是自然数),使得|A|=card A=n
反之无穷集
{a ,b,c}是有穷集,而N、Z、Q、R都是无穷集.

7.包含排斥原理:

例: