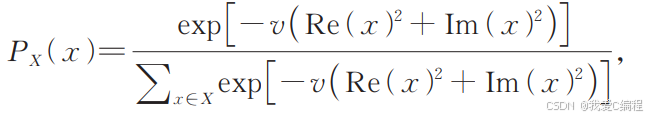基于遗传算法的256QAM星座图的最优概率整形matlab仿真,对比优化前后整形星座图和误码率

1.算法仿真效果

2.算法涉及理论知识概要

3.MATLAB核心程序

4.完整算法代码文件获得

1.算法仿真效果

matlab2022a仿真结果如下（完整代码运行后无水印）：

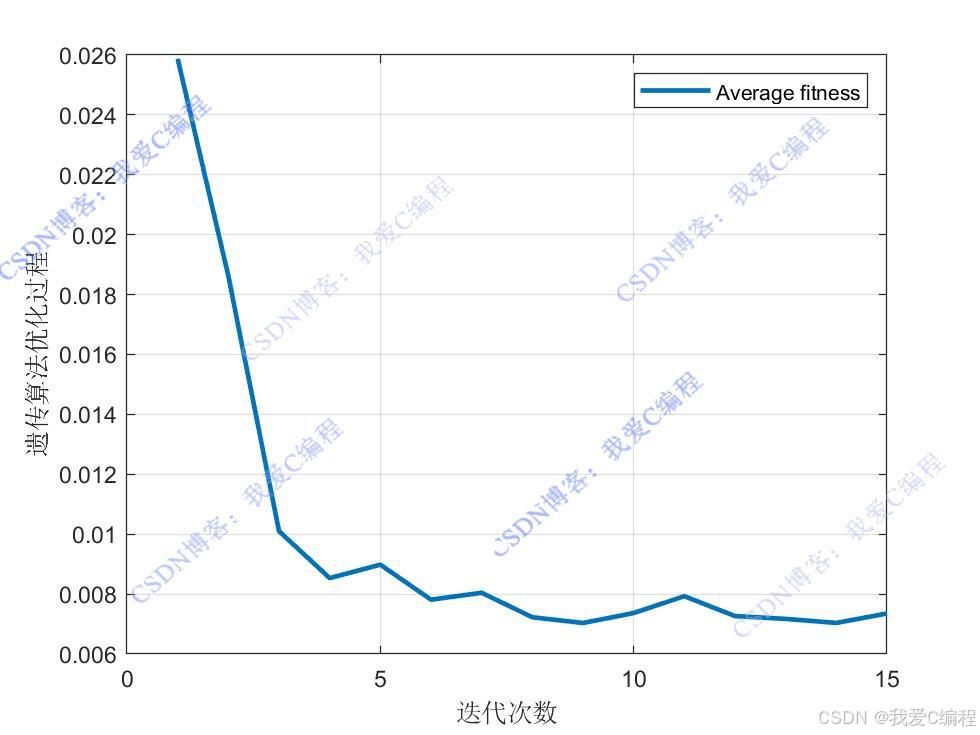
GA优化曲线：

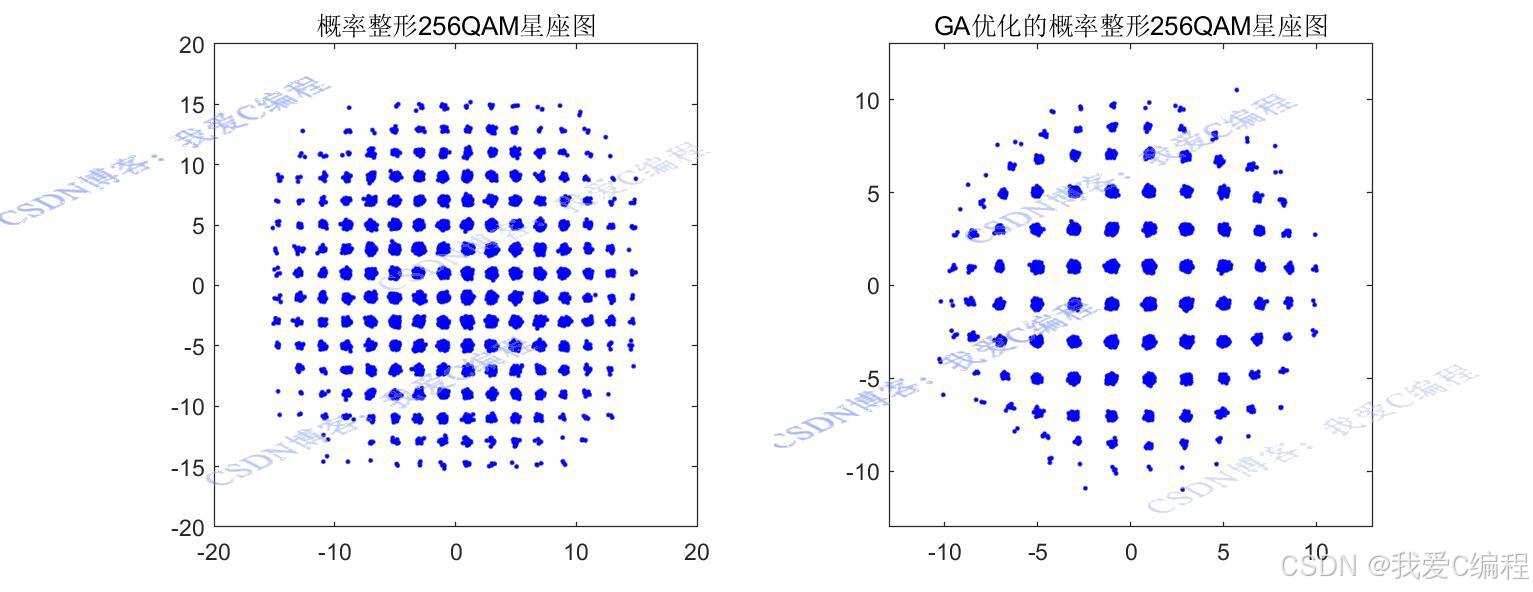
优化前后星座图对比

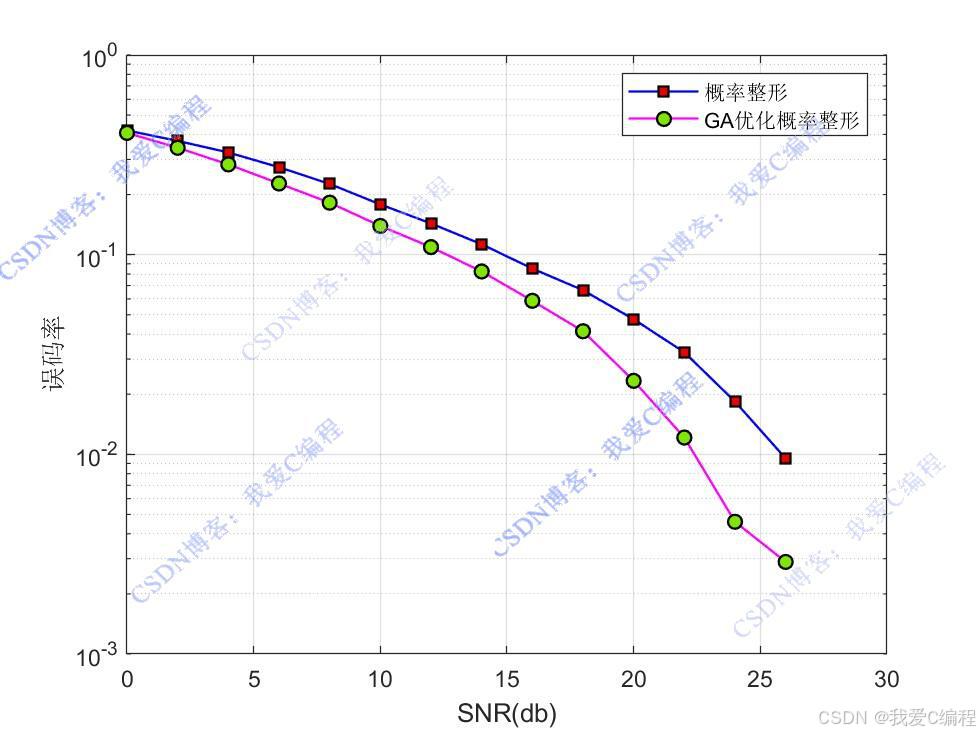
优化前后误码率对比

仿真操作步骤可参考程序配套的操作视频。

2.算法涉及理论知识概要

256QAM 是一种高阶调制方式，星座图中有256个星座点，每个星座点对应 8 比特信息。传统的 256QAM 采用均匀分布。通过改变改变星座图不同位置符号出现的概率，让外圈星座点出现频率降低，有利于减小平均功率，相当于增加了最小欧氏距离，从而有更好的传输性能。这就是我们所说的概率星座整形（PCS）了。它究竟有什么好处呢？

1. 具有整形增益。

2. 有望达到更高的传输容量，显著提升频谱效率。

3. 传输速率可以灵活调整，以完美适配不同的传输信道。

4. 无须多种支持多种QAM映射，仅使用方形QAM调制，需调整整形系数

PCS的关键在于如何对均匀概率的输出映射成非均匀概率幅度分布，而且该概率分布还应该是最优的。理论上可以证明Maxwell-Boltzman分布对于方形QAM整形是最优的概率分布。概率星座整形一般使用如下的公式完成：

参数v为整形因子。在本课题中，将通过GA优化算法，搜索最佳的参数v，进一步提升概率整形后的系统性能。以 256QAM 的误码率（BER）作为适应度函数。误码率越低，表明该概率整形因子对应的星座点概率分布越优。在实际计算时，可通过蒙特卡罗仿真来估计误码率。具体步骤为：依据当前的计算每个星座点的发送概率，生成大量发送符号，经过加性高斯白噪声（AWGN）信道传输，接收符号并进行解调，统计错误比特数，进而计算误码率。

通过GA算法，获得最优的参数v，以降低256QAM 的误码率。

3.MATLAB核心程序

................................................................
MAXGEN = 15;
NIND   = 20;
Nums   = 1; 
Chrom  = crtbp(NIND,Nums*10);
 
%sh
Areas = [];
for i = 1:Nums
    Areas = [Areas,[0;0.25]];% 优化概率整形参数v
end
FieldD = [rep([10],[1,Nums]);Areas;rep([0;0;0;0],[1,Nums])];
 
gen   = 0;
for a=1:1:NIND 
    %计算对应的目标值
    X       = rand(1,Nums)/10;%初始值
    [epls]  = func_obj(X);
    E       = epls;
    Js(a,1) = E;
end
 
Objv  = (Js+eps);
gen   = 0; 
 
%%
while gen < MAXGEN  
      gen
      Pe0 = 0.998;
      pe1 = 0.002; 
 
      FitnV=ranking(Objv);    
      Selch=select('sus',Chrom,FitnV);    
      Selch=recombin('xovsp', Selch,Pe0);   
      Selch=mut( Selch,pe1);   
      phen1=bs2rv(Selch,FieldD);   
 
      for a=1:1:NIND  
          X     = phen1(a,:);
          %计算对应的目标值
          [epls]= func_obj(X);
          E       = epls;
          JJ(a,1) = E;
      end 
      
      Objvsel=(JJ);    
      [Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);   
      gen=gen+1; 
 
      %保存参数收敛过程和误差收敛过程以及函数值拟合结论
 
      Error(gen) = mean(JJ) ;
      [V,I]      = min(JJ);
 
      VVV(gen)   = phen1(I,:);
      VVV2(gen)  = mean2(phen1) ;
end 
 
figure;
plot(Error,'linewidth',2);
grid on
xlabel('迭代次数');
ylabel('遗传算法优化过程');
legend('Average fitness');
 
[V,I] = min(JJ);
VV     = phen1(I,:);
 
 
save GA_OPT.mat Error VV 
0X_077m