【问题描述】
常见的0-1背包问题,多使用二维数组来实现。二维数组实现时,常用的状态转移方程为:
c[i][j]=c[i-1][j], j<vol[i]
c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i]), j>=vol[i]其中,c[i][j]表示“将前i件物品放入容量为j的背包中的最大价值”,vol[i]表示第i件物品的体积,val[i]表示第i件物品的价值。
显然,使用二维数组来实现的0-1背包问题,在背包容量过大时,很容易导致二维数组空间过大,爆空间。因此,可采用空间优化版本的0-1背包问题解法,即使用一维数组进行空间优化。
为了实现“0-1背包问题的一维数组优化”,需解决两个问题:
1.为什么能够利用一维数组优化0-1背包问题?
2.如何利用一维数组优化0-1背包问题?
【问题解析】
为了方便分析,现将0-1背包问题二维数组实现的核心代码重写如下:
//0-1背包问题二维数组实现的核心代码
for(int i=1; i<=n; i++) {
for(int j=1; j<=V; j++) {
//If the current backpack can't hold the i-th item, the value is equal to the previous i-1 item
if(j<vol[i]) c[i][j]=c[i-1][j];
//If yes, the decision is made whether to select item i
else c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i]);
}
}上述核心代码来源于:https://blog.csdn.net/hnjzsyjyj/article/details/125987923
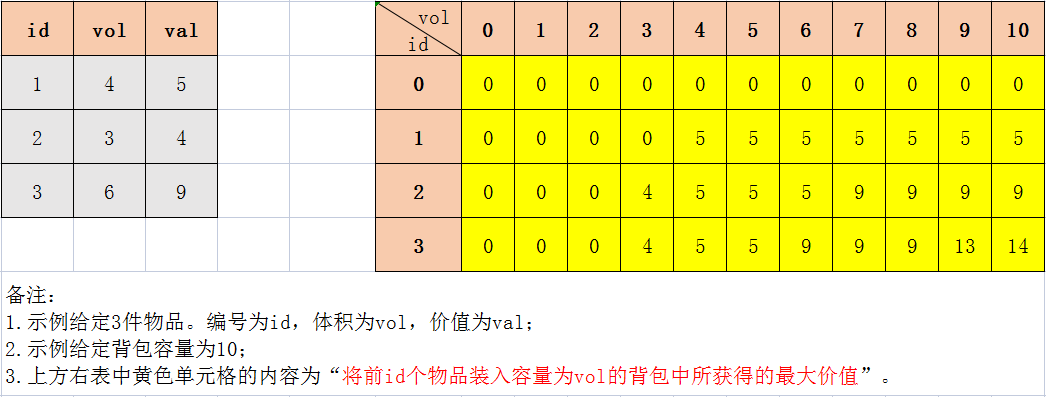
根据0-1背包问题二维数组实现的核心代码,下图给出了n=3,V=10时的c[i][j]的值。即下图中黄色格子中的值。
显然,根据0-1背包问题二维数组实现的核心代码及上图可知:
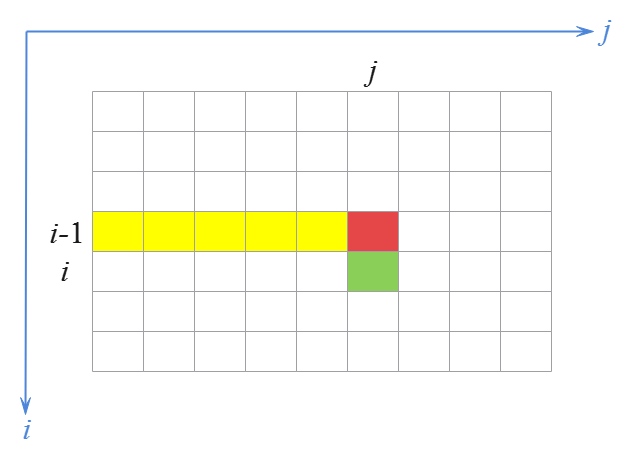
1. 依据是否满足条件 j<vol[i],我们仅需基于第 i-1 层的 c[i-1][j] 或 c[i-1][j-vol[i]] 的值便可对第 i 层的 c[i][j] 的值做出更新,而用不到其他层的值。而且由于0-1背包问题二维数组实现的核心代码采用了二维数组,依据其状态转移方程可知,在更新 c[i][j] 后,第 i-1 层 c[i-1][...] 的值会保留,不会被覆盖。显然,在经过多轮运算后,会保留所有 0~n 层的值。但是,针对仅需要求出最优解的值而不需给出最优方案的0-1背包问题,保留这些层的值也没什么意思。
2. 通过观察0-1背包问题二维数组实现的状态转移方程,还可发现在更新第 i 层的 c[i][j] 的值时,需要用到的第 i-1 层的 c[i-1][j] 或 c[i-1][j-vol[i]] 的第2维的 j 和 j-vol[i] 都是小于等于 j 的,即依据背包容量 j 从大到小的方向进行更新,而不是随机的。如下图所示。这种特性,保证了更新时的有向性。这种性质是保证能够使用动态规划方法的一个必备条件。
因此,根据上面两条的分析,通过降维构建一个一维数组 c[0~V] 便可实现0-1背包问题所需的存储需求,这就是所谓通过降维达到优化空间的方法。下图中黄色单元格的值便是 c[0~V] 的值,即将物品放入容量为 vol (vol=0~V)的背包中时,所获得的最大价值。
在这种设计下,每更新一次就覆盖一次一维数组的值。这非常类似于街头的滚动广告条,即随着时间的推移,新的广告会不断覆盖旧的广告。因此,这个构建的一维数组也常被称为“滚动数组”。
显然,上面的分析回答了上文中提出的问题“1.为什么能够利用一维数组优化0-1背包问题?”。
根据上面的分析,在代码实现上,我们可以将 i 这维直接删去。此时,0-1背包问题二维数组实现的核心代码就转化为:
for(int i=1; i<=n; i++) {
for(int j=1; j<=V; j++) {
if(j<vol[i]) c[j]=c[j]; // 恒成立,可删
else c[j]=max(c[j],c[j-vol[i]]+val[i]); // j>=vol[i] 时执行
}
}可见,上面代码中的 else 语句在满足条件 j>=vol[i] 时才执行,所以所有 0~vol[i] 范围内的数是没有意义的。故上面代码中的内层 for 循环的循环变量 j 的值就可以直接从 j=vol[i] 开始。故而,上面代码可以进一步修改为:
for(int i=1; i<=n; i++) {
for(int j=vol[i]; j<=V; j++) {
c[j]=max(c[j],c[j-vol[i]]+val[i]); // j>=vol[i] 时执行
}
}似乎还不错。但是,问题来了。一维优化后的状态转移方程 c[j]=max(c[j],c[j-vol[i]]+val[i]) 就真的等价于二维实现的状态转移方程 c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i]) 吗?内层循环变量 j 从第 i 件物品体积 vol[i] 到 背包容量 V 的顺序(从小到大)进行遍历,真的可行吗?
仔细观察比较0-1背包问题的状态转移方程:
c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i]) <———— 二维实现
c[j]=max(c[j],c[j-vol[i]]+val[i]) <———— 一维实现
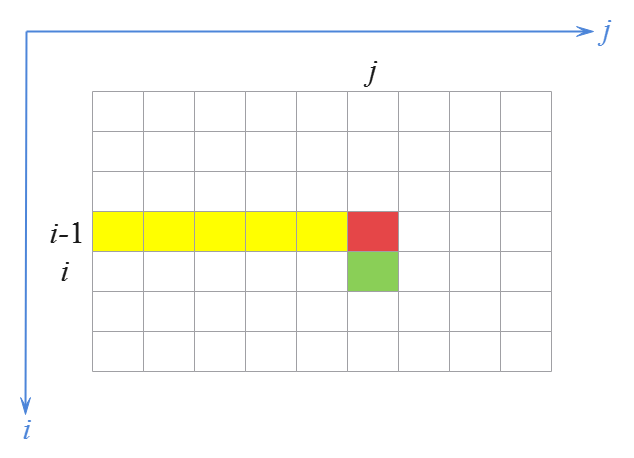
可以发现,在0-1背包问题的二维实现中,当前格子 [i][j](绿色)的值,只和其正上方格子[i-1][j](紫色)的值,及其上一行中的某个黄色格子的值有关。且更新方向为“依据背包容量 j 从大到小的方向”进行更新。为方便学习,将前文中相关的图重绘如下。
而0-1背包问题的一维实现的状态转移方程 c[j]=max(c[j],c[j-vol[i]]+val[i]) ,是与0-1背包问题的二维实现的状态转移方程 c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i]) 一脉相承的,只不过是隐去了二维实现中二维数组的第一维,即 i 维而已。因此,在本质上,0-1背包问题的一维实现和二维实现的原理是一致的。所以,这就可以推出0-1背包问题的一维实现的更新方向也必须为“依据背包容量 j 从大到小的方向”进行更新。
这就回答了上文中提出的问题“2.如何利用一维数组优化0-1背包问题?”。
综上,可得0-1背包问题一维数组优化的核心代码如下:
//0-1背包问题一维数组优化的核心代码
for(int i=1; i<=n; i++) {
for(int j=V; j>=vol[i]; j--) {
c[j]=max(c[j],c[j-vol[i]]+val[i]); // j>=vol[i] 时执行
}
}
【参考文献】
https://blog.csdn.net/chenwenqqqq/article/details/119022170
https://www.bilibili.com/video/BV1Yq4y1m7vF
https://www.bilibili.com/video/BV1QU4y1g7ky
https://blog.csdn.net/weixin_44176696/article/details/105209974