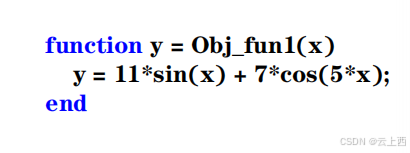该博客为个人学习清风建模的学习笔记,代码全部摘自清风老师,部分课程可以在B站: 【强烈推荐】清风:数学建模算法、编程和写作培训的视频课程以及Matlab等软件教学_哔哩哔哩_bilibili
目录
| 名称 | 重要性 | 难度 |
| 粒子群算法 | ★★★★ | ★★★★ |
数模比赛中,经常见到有同学“套用”启发式算法 ( 数模中常称为 智能优化算法)去求解一些数模问题,事实上,很大一部分问题是 不需要用到启发式算法求解的, Matlab 中内置的函数足够我们使用 了。但是如果遇到的优化问题特别复杂的话,启发式算法就是我们 求解问题的一大法宝。今天就来学习第一个智能优化算法:粒子群算法,其全称 为粒子群优化算法 (Particle Swarm Optimization,PSO) 。它是通过模 拟鸟群觅食行为而发展起来的一种基于群体协作的搜索算法。主要侧重学习其思想,并将其用于求解函数的最值问题,使用算法求解几类较难处理的优化类问题。
1前言
1.1启发式算法
启发式算法百度百科上的定义:一个基于直观或经验构造的算法,在 可接受的花费 下给出待解决 优化问题 的一个 可行解 。( 1 )什么是可接受的花费?计算时间和空间能接受(求解一个问题要几万年 or 一万台电脑)( 2 )什么是优化问题?工程设计中优化问题( optimization problem )指在一定约束条件下 , 求解一个目标函数的最大值( 或最小值 ) 问题。注:实际上和我们之前学过的规划问题的定义一样,称呼不同而已。( 3 )什么是可行解?得到的结果能用于工程实践(不一定非要是最优解)注: “智能算法”是指在工程实践中提出的一些比较“新颖”的算法或理论,因此智能算法的范围要比启发式算法更大一点,如果某种智能算法可以用来解决优化问题,那么这种算法也可能认为是启发式算法。常见的启发式算法:粒子群、模拟退火、遗传算法 、蚁群算法、禁忌搜索算法等等(启发式算法解决的问题大同小异,只要 前三个算法 学会了在数学建模中就足够了)
1.2盲目搜索和启发式搜素
1.2.1盲目搜素
有什么问题?如果现在要求最值的函数是一个多变量的函数,例如是一个 10 个变量的函数,那么就完蛋了!(要考虑的情况随着变量数呈指数增长,计算时间肯定不够)
1.2.2启发式搜素
按照预定的策略实行搜索,在搜索过程中获取的中间信息 不用来 改进策略,称为盲目搜索;反之, 如果利用 了中间信息来改进搜索策略则称为启发式搜索。例如:蒙特卡罗模拟用来求解优化问题就是盲目搜索,还有大家熟悉的枚举法也是盲目搜索。• 关于“启发式”,可以简单总结为下面两点:• 1) 任何有助于找到问题的最优解,但不能保证找到最优解的方法均是启发式方法;• 2) 有助于加速求解过程和找到较优解的方法是启发式方法。
1.3学习智能算法的原因
从“比赛”的角度出发:( 1 ) TSP( 旅行商问题 ) 这类组合优化问题( 2 )非线性整数规划问题(例如书店买书问题)之前学过的蒙特卡罗模拟实际上是随机找解来尝试,如果解集中存在的元素特别多,那么效果就不理想。从“学习”的角度出发:( 1 )训练最优化的思维( 2 )提高自身的编程水平( 3 )各个专业都有广泛应用
2粒子群算法的介绍
它的核心思想是利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得问题的可行解。
2.1直观解释
设想这样一个场景:一群鸟在搜索食物假设:( 1 )所有的鸟都不知道食物在哪( 2 )它们知道自己的当前位置距离食物有多远( 3 )它们知道离食物最近的鸟的位置那么想一下这时候会发生什么?首先,离食物最近的鸟会对其他的鸟说:兄弟们,你们快往我这个方向来,我这离食物最近;与此同时,每只鸟在搜索食物的过程中,它们的位置也在不停变化,因此每只鸟也知道自己离食物最近的位置,这也是它们的一个参考;最后,鸟在飞行中还需要考虑一个惯性。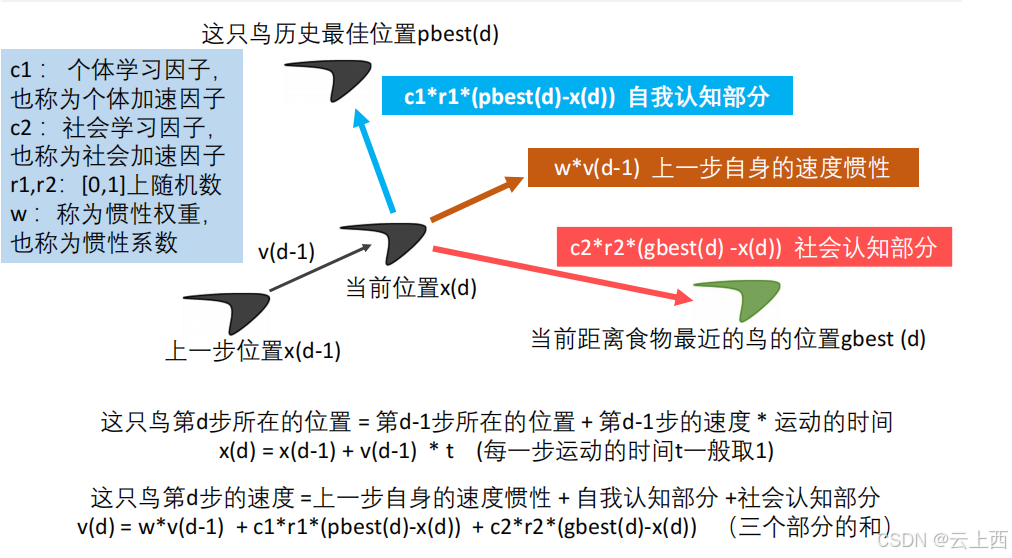
2.2基本概念
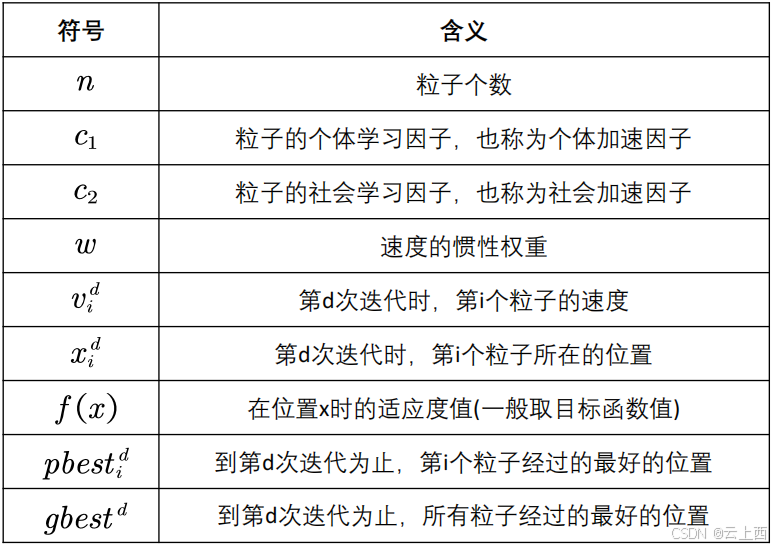
粒子 :优化问题的候选解 位置 :候选解所在的位置 速度 :候选解移动的速度 适应度 :评价粒子优劣的值,一般设置为目标函数值 个体最佳位置 :单个粒子迄今为止找到的最佳位置 群体最佳位置 :所有粒子迄今为止找到的最佳位置
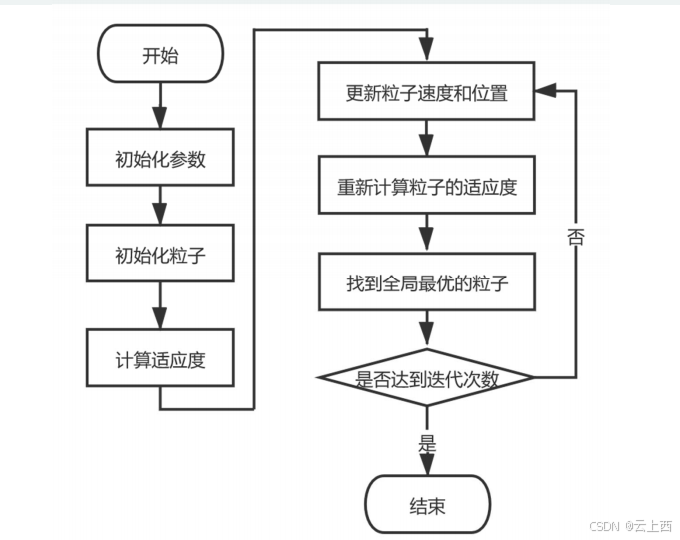
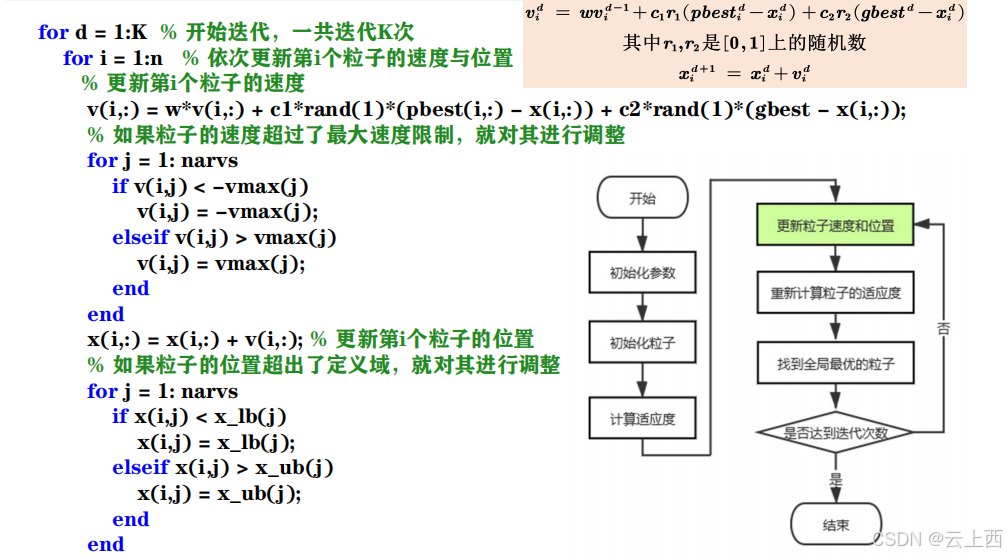
2.3算法流程
2.4核心公式
2.5学习因子
2.6惯性权重
3求解函数最值
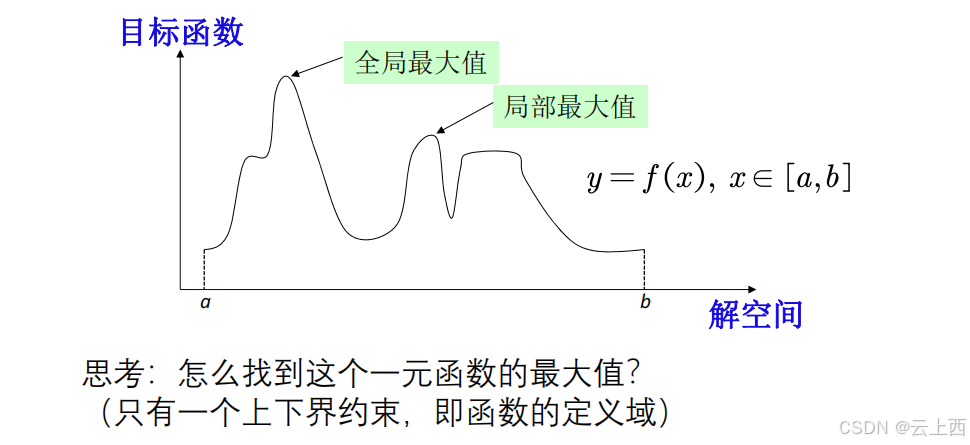
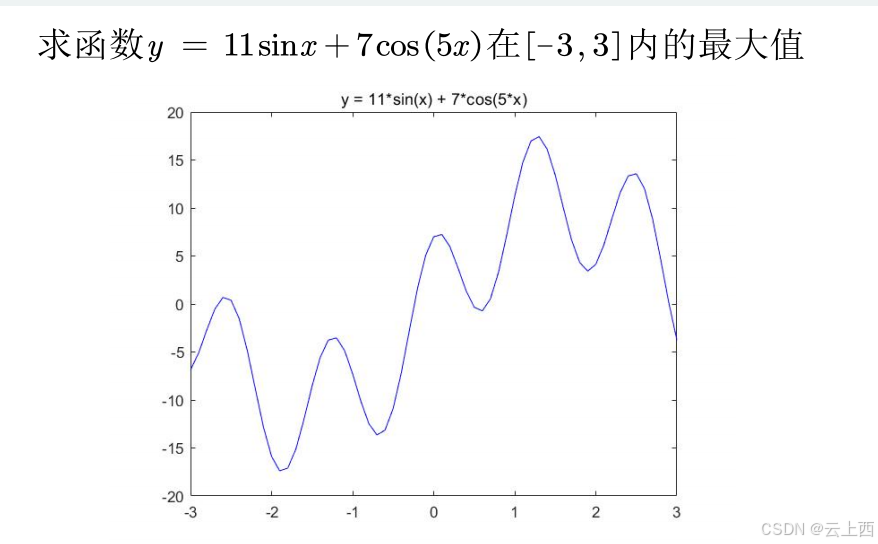
3.1求一元函数最大值
用我们之前学过的函数解决:
如果把初始值改为x0 = 2,结果会是什么?x = 2.4638,fval =13.6847(局部最大值)因此引入粒子群法重新计算:
3.1.1初始化参数
注意:假设目标函数是二元函数,且 x1 和 x2都位于-3 至 3 之间,则 :(1) narvs = 2(2) x_lb=[-3 -3]; x_ub=[3 3]; vmax=[1.2 1.2]
3.1.2初始化粒子
注意:这种写法只支持2017及之后的Matlab,老版本的同学请自己使用repmat函数将向量扩充为矩阵后再运算。
3.1.3计算适应度
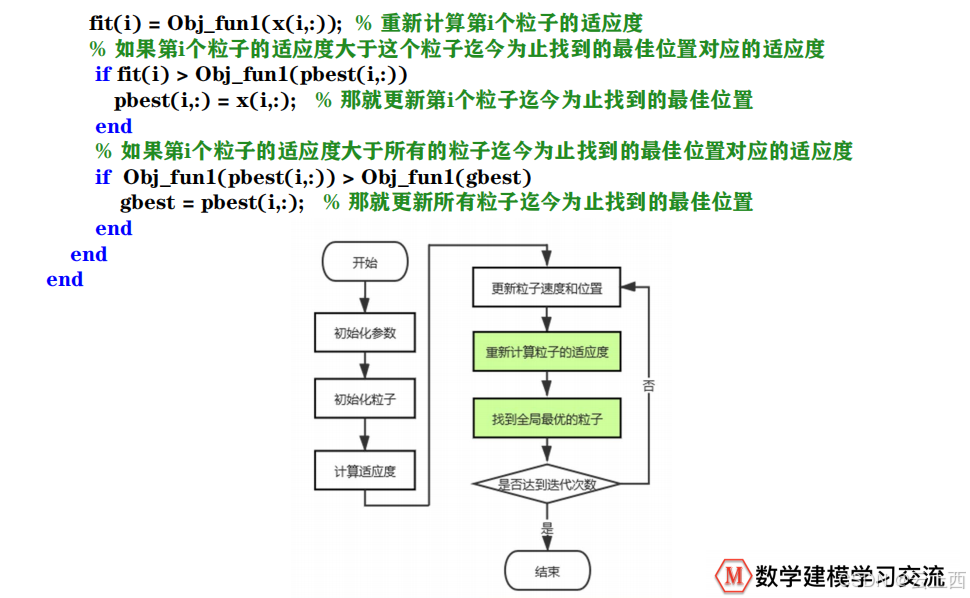
注意:( 1 )这里的适应度实际上就是我们的目标函数值。( 2 )这里可以直接计算出 pbest和gbest ,在后面将用于计算粒子的速度以更新粒子的位置。
3.1.4更新粒子速度和位置
3.1.5重新计算粒子的适应度
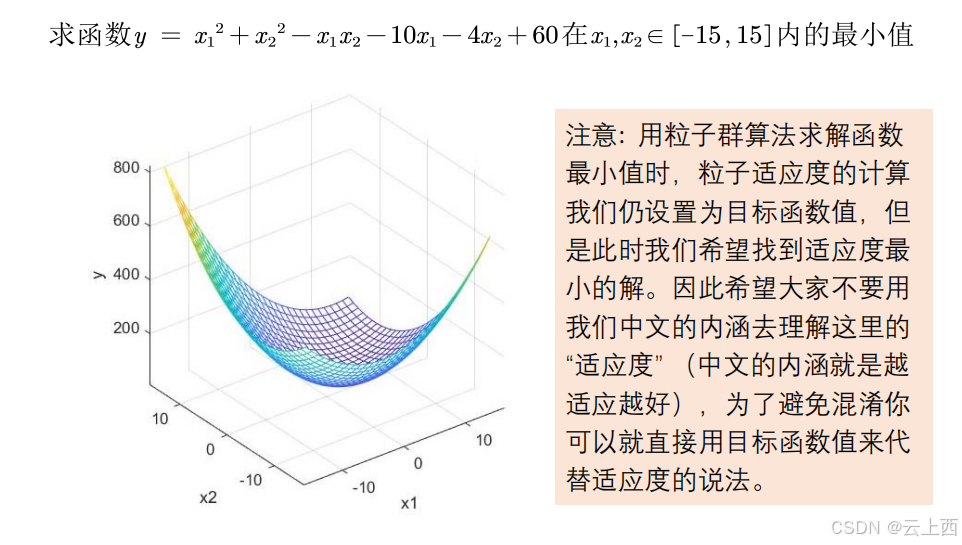
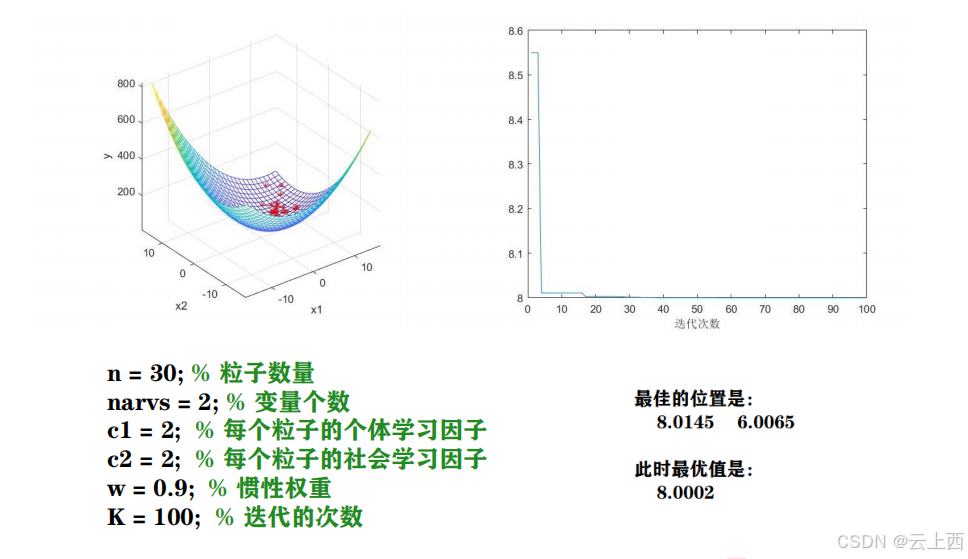
3.2求二元函数最小值
4改进
4.1递减惯性权重
三种递减惯性权重的图形:
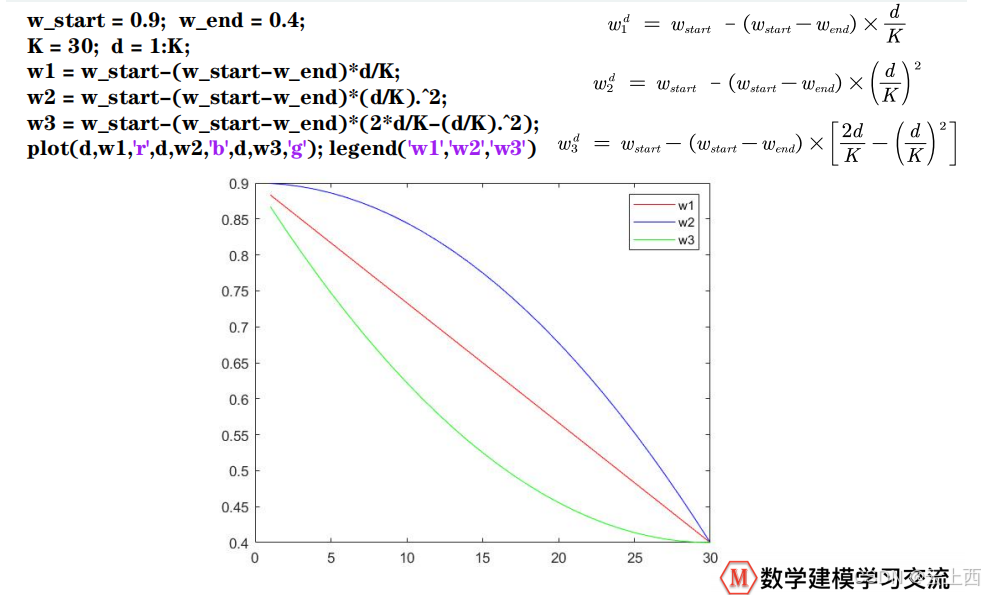
4.2自适应惯性权重
与原来的相比,现在惯性权重和迭代次数以及每个粒子适应度有关
4.2.1求最小值问题

4.2.2求最大值问题
4.3随机惯性权重
使用随机的惯性权重,可以避免在迭代前期局部搜索能力的不足; 也可以避免在迭代后期全局搜索能力的不足。
4.4压缩因子法
4.5非对称学习因子
5优化问题的测试函数
5.1粒子群算法的求解
%% 自适应权重且带有收缩因子的粒子群算法PSO: 求解四种不同测试函数的最小值(动画演示)
clear; clc
%% 粒子群算法中的预设参数(参数的设置不是固定的,可以适当修改)
tic % 开始计时
n = 1000; % 粒子数量
narvs = 30; % 变量个数
c1 = 2.05; % 每个粒子的个体学习因子,也称为个体加速常数
c2 = 2.05; % 每个粒子的社会学习因子,也称为社会加速常数
C = c1+c2;
fai = 2/abs((2-C-sqrt(C^2-4*C))); % 收缩因子
w_max = 0.9; % 最大惯性权重,通常取0.9
w_min = 0.4; % 最小惯性权重,通常取0.4
K = 1000; % 迭代的次数
% Sphere函数
vmax = 30*ones(1,30); % 粒子的最大速度
x_lb = -100*ones(1,30); % x的下界
x_ub = 100*ones(1,30); % x的上界
% Rosenbrock函数
% vmax = 10*ones(1,30); % 粒子的最大速度
% x_lb = -30*ones(1,30); % x的下界
% x_ub = 30*ones(1,30); % x的上界
% Rastrigin函数
% vmax = 1.5*ones(1,30); % 粒子的最大速度
% x_lb = -5.12*ones(1,30); % x的下界
% x_ub = 5.12*ones(1,30); % x的上界
% Griewank函数
% vmax = 150*ones(1,30); % 粒子的最大速度
% x_lb = -600*ones(1,30); % x的下界
% x_ub = 600*ones(1,30); % x的上界
%% 初始化粒子的位置和速度
x = zeros(n,narvs);
for i = 1: narvs
x(:,i) = x_lb(i) + (x_ub(i)-x_lb(i))*rand(n,1); % 随机初始化粒子所在的位置在定义域内
end
v = -vmax + 2*vmax .* rand(n,narvs); % 随机初始化粒子的速度(这里我们设置为[-vmax,vmax])
%% 计算适应度
fit = zeros(n,1); % 初始化这n个粒子的适应度全为0
for i = 1:n % 循环整个粒子群,计算每一个粒子的适应度
fit(i) = Obj_fun3(x(i,:)); % 调用Obj_fun3函数来计算适应度
end
pbest = x; % 初始化这n个粒子迄今为止找到的最佳位置(是一个n*narvs的向量)
ind = find(fit == min(fit), 1); % 找到适应度最小的那个粒子的下标
gbest = x(ind,:); % 定义所有粒子迄今为止找到的最佳位置(是一个1*narvs的向量)
%% 迭代K次来更新速度与位置
fitnessbest = ones(K,1); % 初始化每次迭代得到的最佳的适应度
for d = 1:K % 开始迭代,一共迭代K次
for i = 1:n % 依次更新第i个粒子的速度与位置
f_i = fit(i); % 取出第i个粒子的适应度
f_avg = sum(fit)/n; % 计算此时适应度的平均值
f_min = min(fit); % 计算此时适应度的最小值
if f_i <= f_avg
w = w_min + (w_max - w_min)*(f_i - f_min)/(f_avg - f_min);
else
w = w_max;
end
v(i,:) = fai * (w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:))); % 更新第i个粒子的速度
x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
% 如果粒子的位置超出了定义域,就对其进行调整
for j = 1: narvs
if x(i,j) < x_lb(j)
x(i,j) = x_lb(j);
elseif x(i,j) > x_ub(j)
x(i,j) = x_ub(j);
end
end
fit(i) = Obj_fun3(x(i,:)); % 重新计算第i个粒子的适应度
if fit(i) < Obj_fun3(pbest(i,:)) % 如果第i个粒子的适应度小于这个粒子迄今为止找到的最佳位置对应的适应度
pbest(i,:) = x(i,:); % 那就更新第i个粒子迄今为止找到的最佳位置
end
if fit(i) < Obj_fun3(gbest) % 如果第i个粒子的适应度小于所有的粒子迄今为止找到的最佳位置对应的适应度
gbest = pbest(i,:); % 那就更新所有粒子迄今为止找到的最佳位置
end
end
fitnessbest(d) = Obj_fun3(gbest); % 更新第d次迭代得到的最佳的适应度
end
figure(2)
plot(fitnessbest) % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是:'); disp(gbest)
disp('此时最优值是:'); disp(Obj_fun3(gbest))
toc % 结束计时
5.2自动退出迭代循环的改进
当粒子已经找到最佳位置后,再增加迭代次数只会浪费计算时 间,那么我们能否设计一个策略,能够自动退出迭代呢?( 1 )初始化最大迭代次数、计数器以及最大计数值(例如分别取 100, 0, 20 )( 2 )定义“函数变化量容忍度”,一般取非常小的正数,例如 10^(‐6) ;( 3 )在迭代的过程中,每次计算出来最佳适应度后,都计算该适应度和上一次迭代时最佳适应度的变化量( 取绝对值 ) ;( 4 )判断这个变化量和“函数变化量容忍度”的相对大小,如果前者小,则计数器加 1 ;否则计数器清 0 ;( 5 )不断重复这个过程,有以下两种可能 :① 此时还没有超过最大迭代次数,计数器的值超过了最大计数值,那么我们就跳出迭代循环,搜索结束。② 此时已经达到了最大迭代次数,那么直接跳出循环,搜索结束。
5.3深入研究粒子群算法
6MATLAB自带的粒子群函数
注意:(1) 这个函数在 R2014b 版本后推出,之前的老版本 Matlab 中不存在。(2) 这个函数是求最小值的,如果目标函数是求最大值则需要添加负号从而转换为求最小值。
6.1函数的实现细节
6.1.1预设参数的选取
( 1 )粒子个数 SwarmSize默认设置为: min{100,10*nvars}, nvars 是变量个数( 2 )惯性权重 InertiaRange默认设置的范围为: [0.1,1.1] ,注意,在迭代过程中惯性权重会采取自适应措施,随着迭代过程不断调整。( 3 )个体学习因子 SelfAdjustmentWeight默认设置为: 1.49 (和压缩因子的系数几乎相同)( 4 )社会学习因子 SocialAdjustmentWeight默认设置为: 1.49 (和压缩因子的系数几乎相同)( 5 )邻域内粒子的比例 MinNeighborsFraction默认设置为: 0.25 ,由于采取的是邻域模式,因此定义了一个“邻域最少粒子数目”: minNeighborhoodSize = max{2,( 粒子数目 * 邻域内粒子的比例 ) 的整数部分 } ,在迭代开始后,每个粒子会有一个邻域,初始时邻域内的粒子个数( 记为 Q) 就等于“邻域最少粒子数目”,后续邻域内的粒子个数Q 会自适应调整。
6.1.2变量初始化和适应度计算
( 1 )速度初始化 : 和我们之前的类似,只不过最大速度就是上界和下界的差额vmax = ub – lb ; v = ‐vmax + 2*vmax .* rand(n,narvs);( 2 )位置初始化 : 和我们之前的类似会将每个粒子的位置均匀分布在上下界约束内( 3 )计算每个粒子的适应度适应度仍设置为我们要优化的目标函数,由于该函数求解的是最小值问题,因此,最优解应为适应度最小即目标函数越小的解。( 4 )初始化个体最优位置和我们自己写的代码一样,因为还没有开始循环,因此这里的个体最优位置就是我们初始化得到的位置。( 5 )初始化所有粒子的最优位置因为每个粒子的适应度我们都已经求出来了,所以我们只需要找到适应度最低的那个粒子,并记其位置为所有粒子的最优位置。
6.1.3更新粒子速度和位置
6.1.4自适应调整参数
自适应体现在 : 如果适应度开始停滞时,粒子群搜索会从邻域模式向全局模式转换, 一旦适应度开始下降,则又恢复到邻域模式,以免陷入局部最优。 当适应度的停滞 次数足够大时,惯性系数开始逐渐变小,从而利于局部搜索。
6.1.5自动退出迭代循环
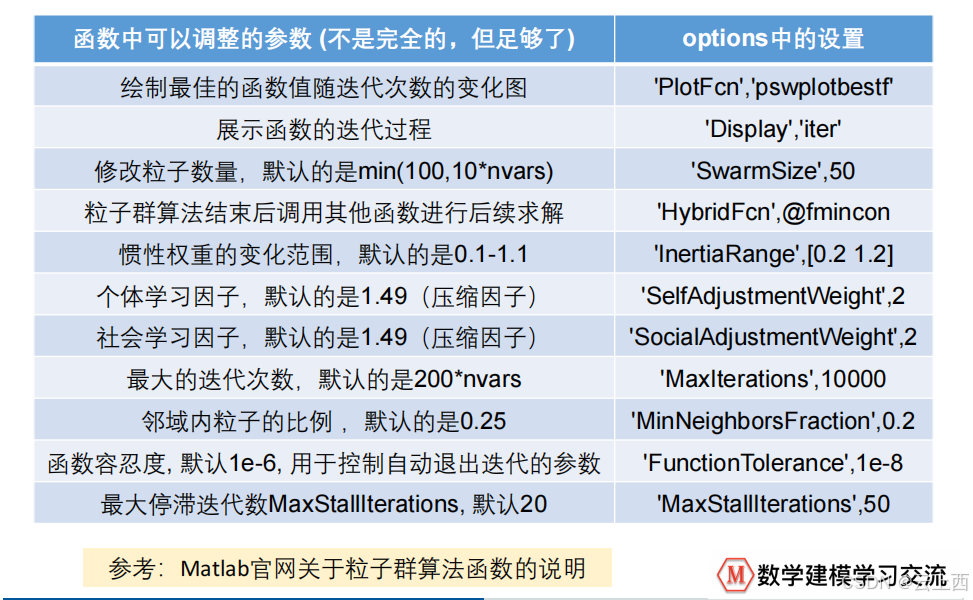
6.2修改函数的参数
6.3函数参数修改的建议
6.4MATLAB代码
%% Matlab自带的粒子群函数 particleswarm
% particleswarm函数是求最小值的
% 如果目标函数是求最大值则需要添加负号从而转换为求最小值。
clear;clc
% Matlab中粒子群算法函数的参考文献
% Mezura-Montes, E., and C. A. Coello Coello. "Constraint-handling in nature-inspired numerical optimization: Past, present and future." Swarm and Evolutionary Computation. 2011, pp. 173–194.
% Pedersen, M. E. "Good Parameters for Particle Swarm Optimization." Luxembourg: Hvass Laboratories, 2010.
% Iadevaia, S., Lu, Y., Morales, F. C., Mills, G. B. & Ram, P. T. Identification of optimal drug combinations targeting cellular networks: integrating phospho-proteomics and computational network analysis. Cancer Res. 70, 6704-6714 (2010).
% Liu, Mingshou , D. Shin , and H. I. Kang . "Parameter estimation in dynamic biochemical systems based on adaptive Particle Swarm Optimization." Information, Communications and Signal Processing, 2009. ICICS 2009. 7th International Conference on IEEE Press, 2010.
%% 求解函数y = x1^2+x2^2-x1*x2-10*x1-4*x2+60在[-15,15]内的最小值(最小值为8)
narvs = 2; % 变量个数
x_lb = [-15 -15]; % x的下界(长度等于变量的个数,每个变量对应一个下界约束)
x_ub = [15 15]; % x的上界
[x,fval,exitflag,output] = particleswarm(@Obj_fun2, narvs, x_lb, x_ub)
%% 直接调用particleswarm函数进行求解测试函数
narvs = 30; % 变量个数
% Sphere函数
% x_lb = -100*ones(1,30); % x的下界
% x_ub = 100*ones(1,30); % x的上界
% Rosenbrock函数
x_lb = -30*ones(1,30); % x的下界
x_ub = 30*ones(1,30); % x的上界
% Rastrigin函数
% x_lb = -5.12*ones(1,30); % x的下界
% x_ub = 5.12*ones(1,30); % x的上界
% Griewank函数
% x_lb = -600*ones(1,30); % x的下界
% x_ub = 600*ones(1,30); % x的上界
[x,fval,exitflag,output] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub)
%% 绘制最佳的函数值随迭代次数的变化图
options = optimoptions('particleswarm','PlotFcn','pswplotbestf')
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 展示函数的迭代过程
options = optimoptions('particleswarm','Display','iter');
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 修改粒子数量,默认的是:min(100,10*nvars)
options = optimoptions('particleswarm','SwarmSize',50);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 在粒子群算法结束后继续调用其他函数进行混合求解(hybrid n.混合物合成物; adj.混合的; 杂种的;)
options = optimoptions('particleswarm','HybridFcn',@fmincon);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 惯性权重的变化范围,默认的是0.1-1.1
options = optimoptions('particleswarm','InertiaRange',[0.2 1.2]);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 个体学习因子,默认的是1.49(压缩因子)
options = optimoptions('particleswarm','SelfAdjustmentWeight',2);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 社会学习因子,默认的是1.49(压缩因子)
options = optimoptions('particleswarm','SocialAdjustmentWeight',2);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 最大的迭代次数,默认的是200*nvars
options = optimoptions('particleswarm','MaxIterations',10000);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 领域内粒子的比例 MinNeighborsFraction,默认是0.25
options = optimoptions('particleswarm','MinNeighborsFraction',0.2);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 函数容忍度FunctionTolerance, 默认1e-6, 用于控制自动退出迭代的参数
options = optimoptions('particleswarm','FunctionTolerance',1e-8);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 最大停滞迭代数MaxStallIterations, 默认20, 用于控制自动退出迭代的参数
options = optimoptions('particleswarm','MaxStallIterations',50);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
%% 不考虑计算时间,同时修改三个控制迭代退出的参数
tic
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',100000);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
toc
%% 在粒子群结束后调用其他函数进行混合求解
tic
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',50,'MaxIterations',20000,'HybridFcn',@fmincon);
[x,fval] = particleswarm(@Obj_fun3,narvs,x_lb,x_ub,options)
toc
7粒子群算法的后续讨论
7.1非线性约束问题
7.2组合优化问题
8求解方程组
8.1方程组一般形式
8.2定义适应度函数(目标函数)
8.3实例
8.3.1vpasolve函数
%% (1)vpasolve函数
clear; clc
syms x1 x2 x3
eqn = [abs(x1+x2)-abs(x3) == 0, x1*x2*x3+18 == 0, x1^2*x2+3*x3 == 0]
[x1, x2, x3] = vpasolve(eqn, [x1, x2, x3], [0 0 0])
[x1, x2, x3] = vpasolve(eqn, [x1, x2, x3], [1 1 1]) % 换一个初始值试试8.3.2fsolve函数
%% (2)fsolve函数
x0 = [0,0,0]; % 初始值
x = fsolve(@my_fun,x0)
% 换一个初始值试试
x0 = [1,1,1]; % 初始值
format long g % 显示更多的小数位数
x = fsolve(@my_fun,x0)
function F = my_fun(x)
F(1) = abs(x(1)+x(2))-abs(x(3));
F(2) = x(1) * x(2) * x(3) + 18;
F(3) = x(1)^2*x(2)+3*x(3);
end8.3.3粒子群算法
%% (3) 粒子群算法(可以尝试多次,有可能找到多个解)
clear; clc
narvs = 3;
% 使用粒子群算法,不需要指定初始值,只需要给定一个搜索的范围
lb = -10*ones(1,3); ub = 10*ones(1,3);
options = optimoptions('particleswarm','FunctionTolerance',1e-12,'MaxStallIterations',100,'MaxIterations',20000,'SwarmSize',100);
[x, fval] = particleswarm(@Obj_fun,narvs,lb,ub,options)
function f = Obj_fun(x)
f1= abs(x(1)+x(2))-abs(x(3)) ;
f2 = x(1) * x(2) * x(3) + 18;
f3= x(1)^2 * x(2) + 3*x(3);
f = abs(f1) + abs(f2) + abs(f3);
end8.3.4总结
结论:
( 1 ) vpasolve 函数和 fsolve 函数需要给定一个比较好的初始值,如果初始值没给好则求不出结果;( 2 )粒子群算法不需要给初始值,只需要给一个搜索的范围。由于算法本身具有随机性,因此可能需要多次运行才能得到一个较好的结果。
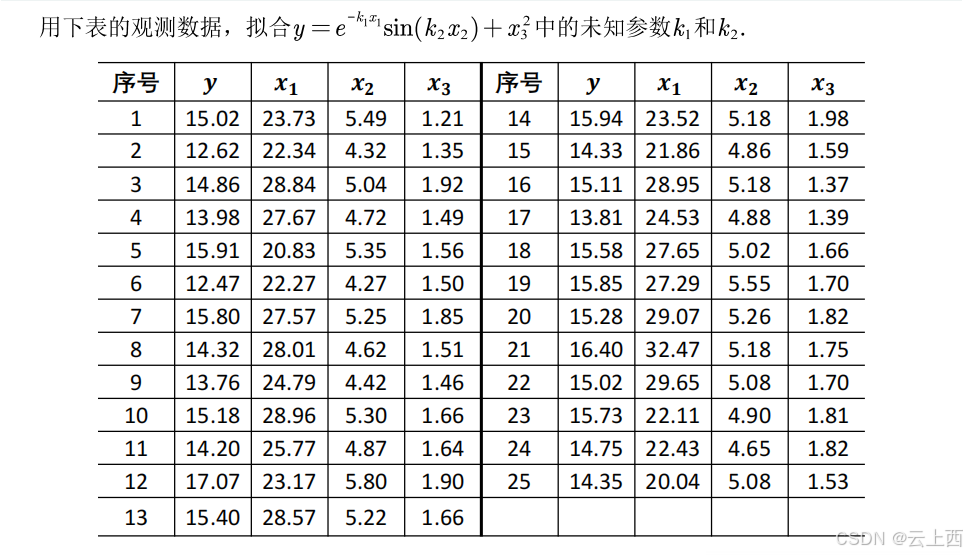
9多元函数拟合

 9.1fmincon函数
9.1fmincon函数

9.2无约束最小值函数
9.3非线性最小二乘拟合函数
9.4粒子群算法
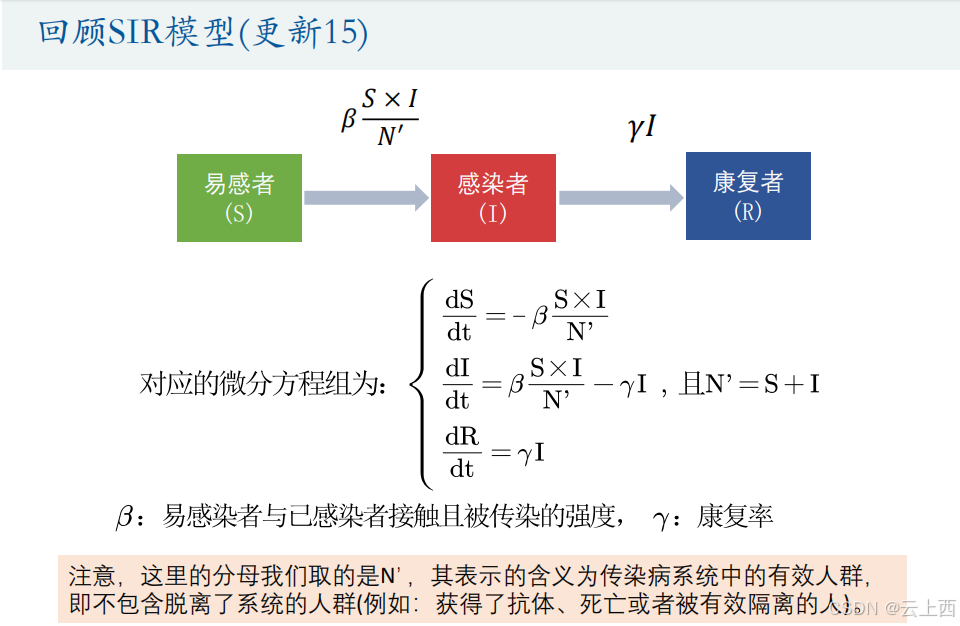
10拟合微分方程
注意:如果微分方程或者微分方程组有解析解( dsolve 函数能求出来),那么这时候就转换为了函数拟合问题,例如 举的美国人口预测问题( 阻滞增长模型 ) ;我们这里讨论的拟合微分方程指的是只能用ode45 这类函数求出数值解的情况。
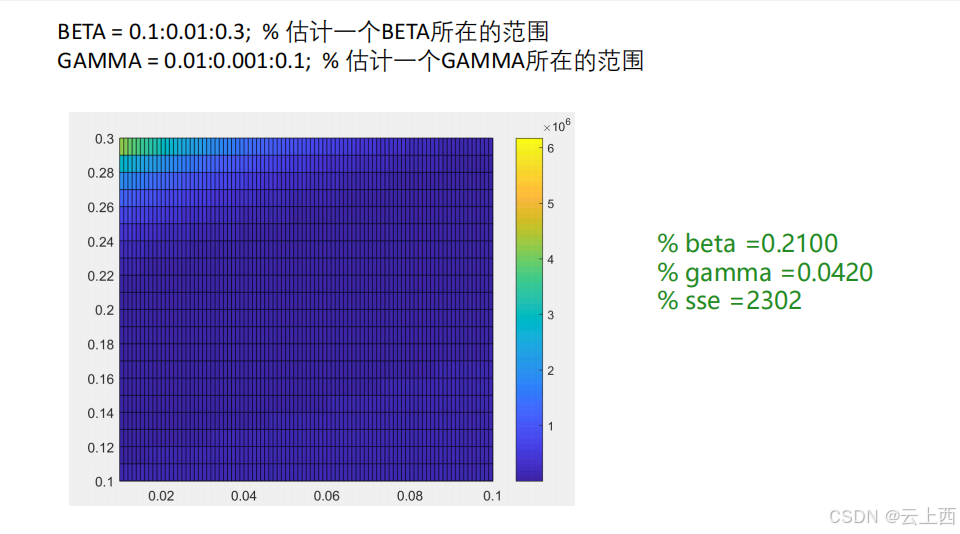
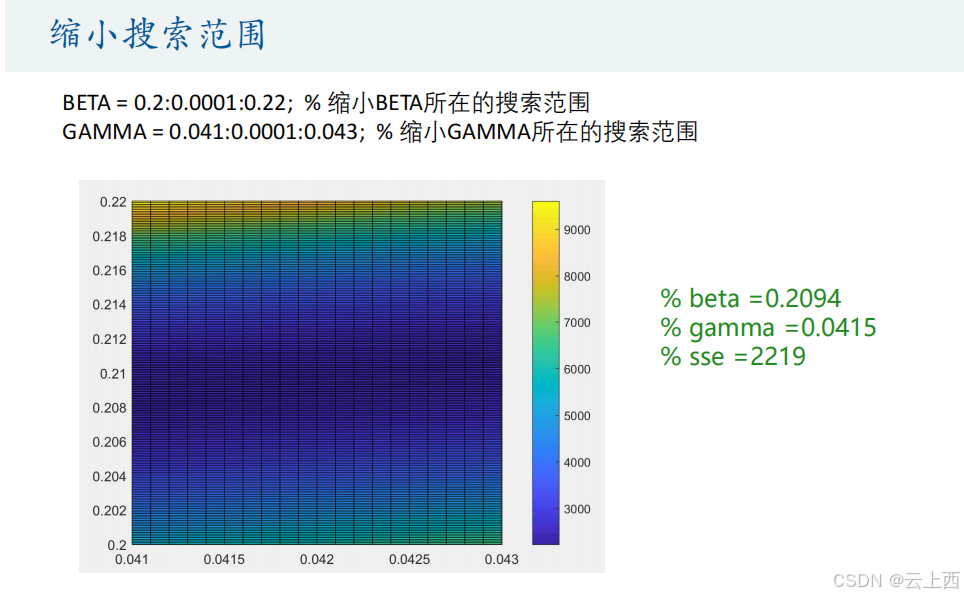
10.1网格搜索
网格搜索法实际上就是枚举法,下面是对它的总结:( 1 )搜索的精度越高(网格划分的越细),搜索耗费的时间越长;( 2 )缩小网格搜索范围(可以减少搜索时间)可能会让我们找到的解陷入局部最优;( 3 )如果我们有多个要搜索的变量,网格搜索法就很难办了,多重循环会大大增加搜索时间。
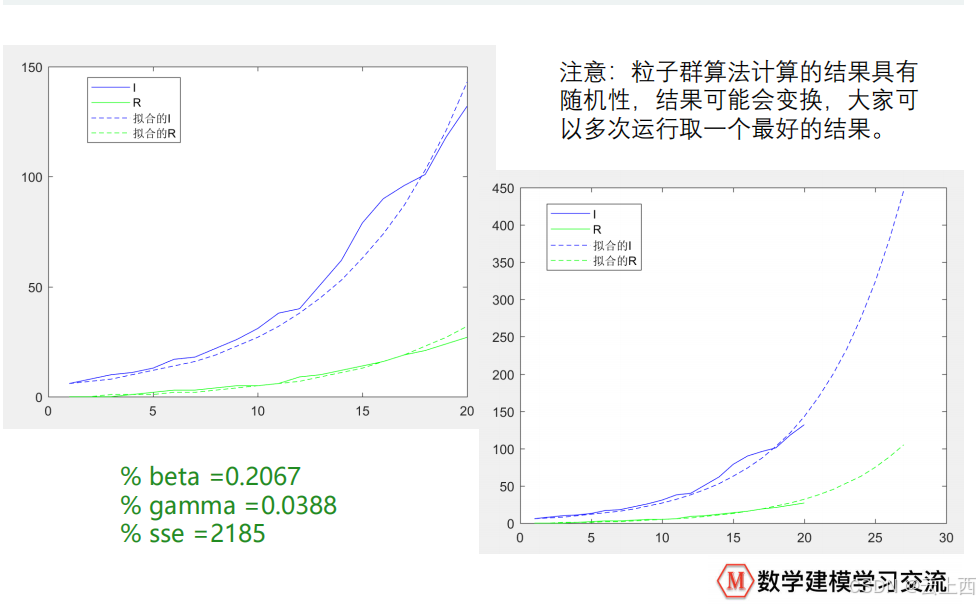
10.2粒子群算法
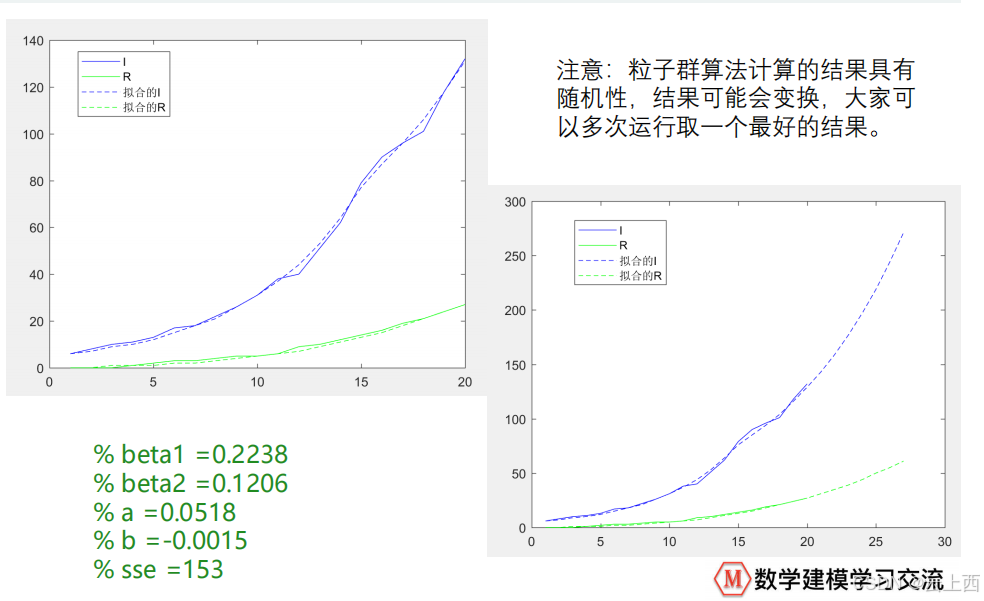
10.3不固定参数求解