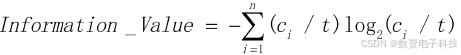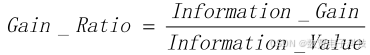嵌入式人工智能应用-第四章决策树 6

1 决策数介绍

决策树是一种机器学习的方法。决策树的生成算法有 ID3, C4.5 和 C5.0 等。决策树是一种树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。

决策树是一种十分常用的分类方法，需要监管学习（有教师的 Supervised Learning），监管学习就是给出一堆样本，每个样本都有一组属性和一个分类结果，也就是分类结果已知，那么通过学习这些样本得到一个决策树，这个决策树能够对新的数据给出正确的分类。

1.1 原理

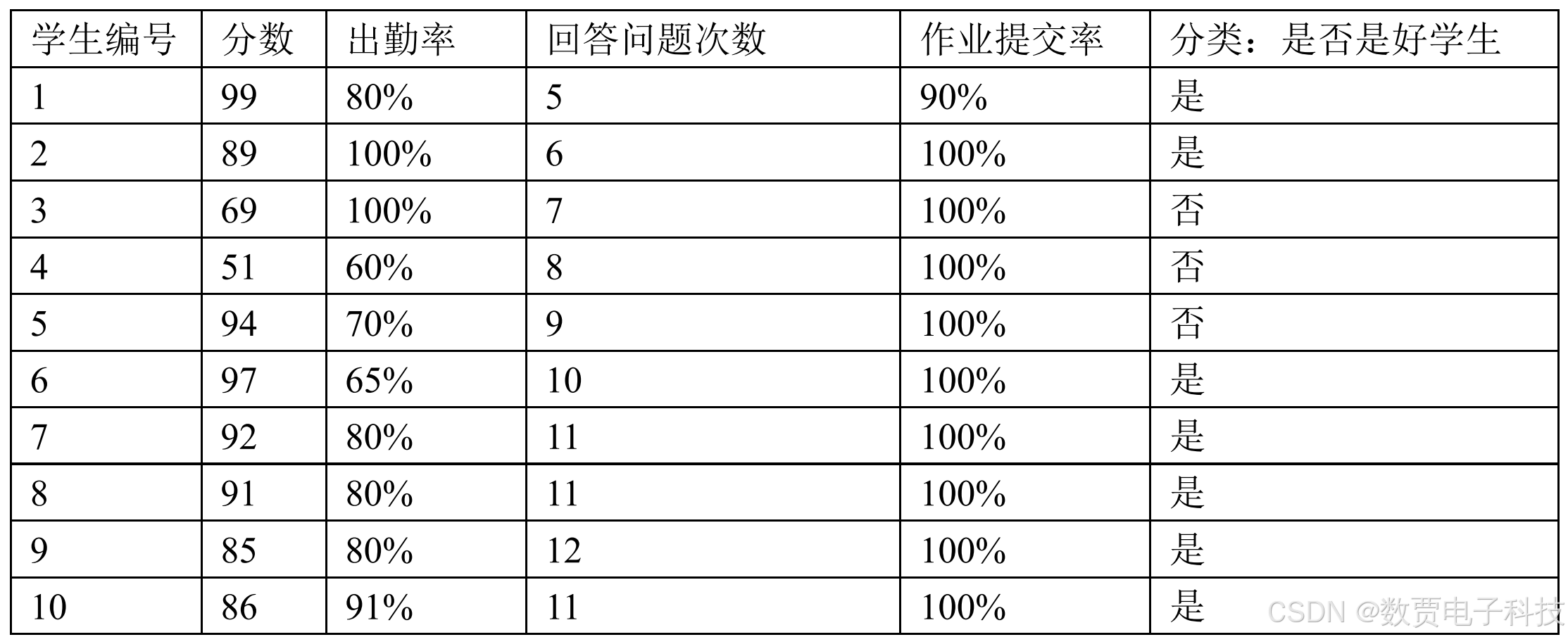
给出如下的一组数据，一共有十个样本（学生数量），每个样本有分数，出勤率，回答问题次数，作业提交率四个属性，最后判断这些学生是否是好学生。最后一列给出了人工分类结果。

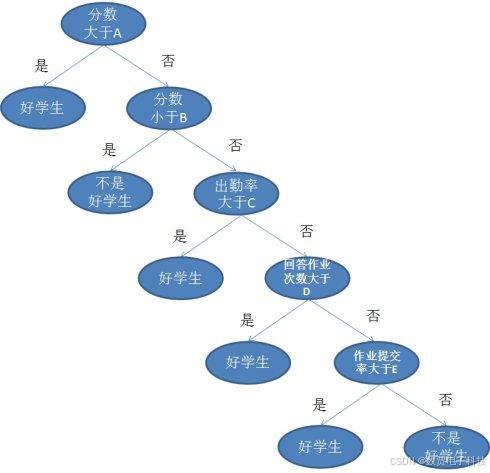
在这里插入图片描述

然后用这一组附带分类结果的样本可以训练出多种多样的决策树，这里为了简化过程，我们假设决策树为二叉树。

在这里插入图片描述
决策树的生成主要分以下两步，这两步通常通过学习已经知道分类结果的样本来实现。1. 节点的分裂：一般当一个节点所代表的属性无法给出判断时，则选择将这一节点分成 2 个子节点（如不是二叉树的情况会分成 n 个子节点）。2. 阈值的确定：选择适当的阈值使得分类错误率最小（Training Error）。

1.2 基于 ID3 的决策树生成算法

由增熵（Entropy）原理来决定哪个做父节点，哪个节点需要分裂。对于一组数据，熵越小说明分类结果越好。熵定义如下：

Entropy＝-sum [p(x_i) * log2(P(x_i) ]

其中 p(x_i) 为 x_i 出现的概率。假如是 2 分类问题，当 A 类和 B 类各占 50%的时候，Entropy = -（0.5log_2( 0.5)+0.5log_2( 0.5))= 1。当只有 A 类，或只有 B 类的时候，Entropy= -（1*log_2（1）+0）=0 。所以当 Entropy 最大为 1 的时候，是分类效果最差的状态，当它最小为 0 的时候，是完全分类的状态。因为熵等于零是理想状态，一般实际情况下，熵介于 0 和 1 之间。熵的不断最小化，实际上就是提高分类
正确率的过程。

单一地通过以下语句分类：

分数小于 70 为【不是好学生】：分错 1 个
出勤率大于 70 为【好学生】：分错 3 个
问题回答次数大于 9 为【好学生】：分错 2 个
作业提交率大于 80%为【好学生】：分错 2 个

最后发现分数小于 70 为【不是好学生】这条分错最少，也就是熵最小，所以应该选择这条为父节点进行树的生成，当然分数也可以选择大于 71，大于 72 等等，出勤率也可以选择小于 60，65 等等，总之会有很多类似上述 1~4 的条件，最后选择分类错最少即熵最小的那个条件。而当分裂父节点时道理也一样，分裂有很多选择，针对每一个选择，与分裂前的分类错误率比较，留下那个提高最大的选择，即熵减最大的选择。

1.3 基于 C4.5 的决策树生成算法

通过对 ID3 的学习，可以知道 ID3 存在一个问题，那就是越细小的分割分类错误率越小，所以 ID3 会越分越细，比如以第一个属性为例：设阈值小于 70 可将样本分为 2 组，但是分错了 1 个。如果设阈值小于70，再加上阈值等于 95，那么分错率降到了 0，但是这种分割显然只对训练数据有用，对于新的数据没有意义，这就是所说的过度学习（Overfitting）。

分割太细了，训练数据的分类可以达到 0 错误率，但是因为新的数据和训练数据不同，所以面对新的数据分错率反倒上升了。决策树是通过分析训练数据，得到数据的统计信息，而不是专为训练数据量身定做。

就比如给人做衣服，叫来 10 个人做参考，做出一件 10 个人都能穿的衣服，然后叫来另外 5 个和前面10 个人身高差不多的，这件衣服也能穿。但是当你为 10 个人每人做一件正好合身的衣服，那么这 10 件衣服除了那个量身定做的人，别人都穿不了。

所以为了避免分割太细，c4.5 对 ID3 进行了改进，C4.5 中，优化项要除以分割太细的代价，这个比值叫做信息增益率，显然分割太细分母增加，信息增益率会降低。除此之外，其他的原理和 ID3 相同。

1.4 基于 C5.0 的决策树生成算法

C5.0 是对 ID3 算法的改进，引入了分支度的概念。分支度的计算公式：
在这里插入图片描述
信息增益率：

在这里插入图片描述
信息增益率其实就是信息增益除以分支度。分支度指若某划分属性 S 将样本 T 划分成 n 个子集 T1,T2,…Tn，则此属性 S 的分支度就等于：每个分支子集 Ti 的个数 ci，除以样本总个数 t，然后再乘以 log2ci/t，然后再把各个分支的计算值加起来。

1.5 CART：分类回归树

CART 是一个二叉树，也是回归树，同时也是分类树，CART 的构成简单明了。CART 只能将一个父节点分为 2 个子节点。CART 用 GINI 指数来决定如何分裂。GINI 指数：总体内包含的类别越杂乱，GINI指数就越大（跟熵的概念很相似）。

a. 比如出勤率大于 70%这个条件将训练数据分成两组：大于 70%里面有两类：【好学生】和【不是好学生】，而小于等于 70%里也有两类：【好学生】和【不是好学生】。

b. 如果用分数小于 70 分来分：则小于 70 分只有【不是好学生】一类，而大于等于 70 分有【好学生】和【不是好学生】两类。

比较 a 和 b，发现 b 的凌乱程度比 a 要小，即 GINI 指数 b 比 a 小，所以选择 b 的方案。以此为例，将所有条件列出来，选择 GINI 指数最小的方案，这个和熵的概念很类似。

CART 还是一个回归树，回归解析用来决定分布是否终止。理想地说每一个叶节点里都只有一个类别时分类应该停止，但是很多数据并不容易完全划分，或者完全划分需要很多次分裂，必然造成很长的运行时间&