思路

按单调栈递增的思路
注意：这里所说的递增按列表的递增去想，不要用栈的从栈顶往下去看（那样就是递减了） 如 [2,4,6,8]即所说的单调栈递增

t:单调递增栈

heights首末尾加上0 : 预防 [2,4,6,8]情况 2无左边最小值 列表数字无右边最小值

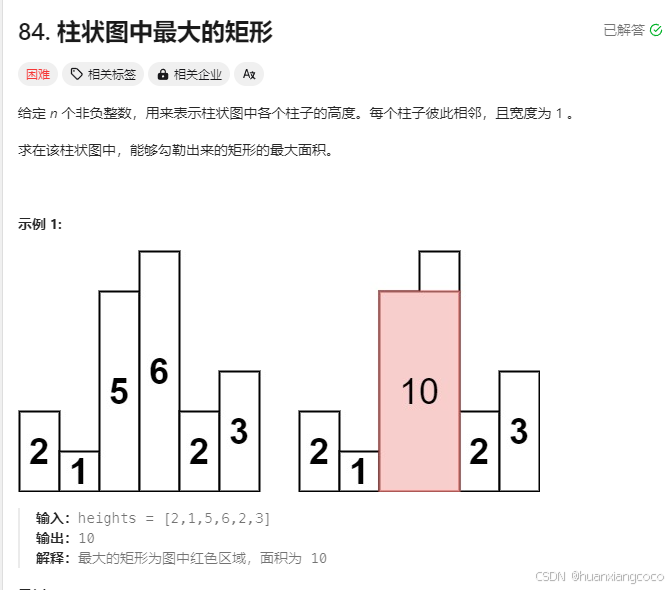
以当前柱子为例，必定是往左、右去找比自己第一个小的柱子，则这些柱子直接的面积即为自己的最大面积，但一个柱子的宽度为1，所以计算总宽度时要-1（我的理解是减去左边那根柱子的宽度）

往左、右找最小柱子则用到单调栈：

首先下标为0入栈（初始化），接着，当前柱子heights[i]大于等于t[-1]位置的值，说明t[-1]右边最小未出现，将当前柱子入栈

当前柱子heights[i]小于t[-1]位置柱子，说明t[-1]位置右边的最小柱子出现了，而t[-1]位置左边最小柱子为t[-2]（单调递增栈）,此时可以计算出以t[-1]位置柱子围成的最大面积

class Solution(object):
    def largestRectangleArea(self, heights):
        """
        :type heights: List[int]
        :rtype: int
        """

      
        t=[]
        #height首末尾加上0 预防 [2,4,6,8]情况   2无左边最小值   列表数字无右边最小值   
        heights.append(0)
        heights.insert(0,0)
        t.append(0)
        i = 1
        res = 0
        while i <len(heights):
            #height[i]<height[t[-1]]  说明t[-1]找到了右边的最小，因为栈是递增的，所有t[-1]左边最小为t[-2]
            while len(t)>0 and heights[i]<heights[t[-1]]:
                area=heights[t.pop()]*(i-t[-1]-1)
                res = max(res,area)

            t.append(i)
            i+=1
        return res

ps
单调栈：递增或递减，本质都是为了栈里的元素服务，即拿栈里的元素进行计算
如本题：当遍历元素时，与栈里元素进行比较，然后计算栈内对应位置柱子可围成的最大面积
又如739 每日温度：遍历温度时，可以计算出当前栈顶元素温度之后的最高温度
这两题栈都是记录下标位置是为了方便计算