关于Python的保留小数问题的探讨——实现真正的“四舍五入”数值修约规则

无论是用过Python的数据格式化输出，还是round()保留小数，相信读者都遇到过困惑的问题。看下面的例子：

对1.375、1.475、3.255、1.125、1.245五个数保留二位小数。

print('%.2f，%.2f，%.2f，%.2f，%.2f ' % (1.375,1.475,3.255,
      1.125,1.245))

结果为：

1.38，1.48，3.25，1.12，1.25

print('{:.2f}，{:.2f}，{:.2f}，{:.2f}，{:.2f}'.format(1.375,
	  1.475,3.255,1.125,1.245))

结果为：

1.38，1.48，3.25，1.12，1.25

print(round(1.375,2),round(1.475,2),round(3.255,2),
           round(1.125,2),round(1.245,2),sep='，')

结果为：

1.38，1.48，3.25，1.12，1.25

用%格式化、format()格式化和round()保留二位小数，结果都相同，1.375、1.475、1.245三个数5进了，1.125、3.255两个数5舍了，好像进与舍没有规律。

经查Python是按奇进偶舍修约规则进行舍入。

奇进偶舍，又称为四舍六入五成双规则，或称银行进位法(Banker's Rounding)，是一种计数保留法，是一种数值修约规则。从统计学的角度，“奇进偶舍”比“四舍五入”更为精确。

所以Python实际操作时是按保留位数之后的数是大于5则“进”，小于5则“舍”，刚好是5则看前一位，是奇数则“进”为偶数，是偶数则“舍”去。

但3.255、1.245好像违反规则，3.255应该进为3.26、1.245应该舍为1.24。为什么会出现反常情况呢?

产生反常的原因是float型是非精确类型，Python float其存储占8字节，最高位63位是符号位，0为正1为负；接着11位是阶位，表示2的次方数(-1024~1023)，实际存储时需加1023；后面52位为尾数，整数恒为1不存储。存储时将十进制浮点数的整数、小数转换为二进制，然后将小数点移动到最左边的1后面，小数点向左移1位指数加1，小数点向右移1位指数减1，参见图1。如果小数可以用有限的52位二进制表示，则此浮点数是可以精确表示原值，如果小数不能用有限的52位二进制表示，则此浮点数就不能精确表示原值，如53位起舍了则会小于原值，如53位起进了则会大于原值。

图1 float型存储格式(以1.245、3.255为例)

1.245：(1.0011111010111000010100011110101110000101000111101100) $_{2}$ × $2^{0}$

=1.2450000000000001065814103640>1.245

第3位小数及以后大于5，所以进上去了。

3.255：(1.1010000010100011110101110000101000111101011100001010) $_{2}$ × $2^{1}$

=1. 6274999999999999467092948180×2

=3.2549999999999998934185896360<3.255

第3位小数及以后小于5，所以舍了没有进。

即使使用decimal模块，浮点数仍不是精确的，只是精度更高。例如：

import decimal
print(decimal.Decimal(1.245))

结果为：

1.24500000000000010658141036401502788066864013671875

即1.245=1.24500000000000010658141036401502788066864013671875>1.245

print(decimal.Decimal(3.255))

结果为：

3.25499999999999989341858963598497211933135986328125

即3.255=3.25499999999999989341858963598497211933135986328125<3.255

虽然奇进偶舍称银行进位法(Banker's Rounding)，从统计学的角度，“奇进偶舍”比“四舍五入”更为精确。但我国财务会计记账是按“四舍五入”数值修约规则，如改用“奇进偶舍”数值修约规则就会与人工计算不一致。那如何在Python中实现真正“四舍五入”数值修约规则呢? 可以用如下简便的方法来实现。

首先要说明十进制小数0.5是可以用52位二进制以内精确表示为0.1，即1*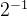 $2^{-1}$ =0.5。所以只要浮点数可以用52位二进制以内表示原值，就不会有误差，即可精确表示。如：

print(decimal.Decimal(1.125))

结果为：

1.125

浮点数1.125是可以用52位二进制以内精确表示为1.001，即1*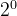 $2^{0}$ +1* $2^{-3}$ =1.125

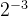
print(decimal.Decimal(1.375))

结果为：

1.375

浮点数1.375是可以用52位二进制以内精确表示为1.011，即 $1*2^{0}+1*2^{-2}+1*2^{-3}$ =1.375

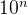
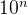
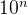
其次如果要将数保留n位小数，则先将待“四舍五入”数放大 $10^{n}$ 倍，加0.5后取整，再缩小 $10^{n}$ 倍。由于放大 $10^{n}$ 倍后，小数部分0.5浮点数能精确表达，加的0.5浮点数也能精确表达。如果小数部分小于0.5，加0.5后小于1，则取整时会舍去；如果小数部分大于等于0.5，加0.5后大于等于1，则取整时会进上去。

但实际上由于浮点数可能不精确，乘以100后仍可能不精确，故可以加0.5000000001，以消除可能带来的误差。如：

print(decimal.Decimal(1.245))

1.24500000000000010658141036401502788066864013671875

print(decimal.Decimal(124.5))

124.5

print(decimal.Decimal(1.245*100))

124.5000000000000142108547152020037174224853515625

print(1.245*100 == 124.5)

False # 导致124.5≠124.5

print(decimal.Decimal(3.255))

3.25499999999999989341858963598497211933135986328125

print(decimal.Decimal(3.255*100))

325.5

print(325.5 == 3.255*100)

True # 不是所有的都不相等, 325.5=325.5=3.255*100

以财务金额保留二位小数为例，设要保留小数的数为x，保留小数后的数为y，则：

y = int(x * 10**2 + 0.5000000001) / 10**2

同样用上面的1.375、1.475、3.255、1.125、1.245五个数，再加3.254999999, 3.255000001进行测试(3.254999999<3.255, 3.255000001>3.255)。

lst = [1.375, 1.475, 3.255, 1.125, 1.245, 3.254999999, 3.255000001]
for i in lst:
    y = int(i * 10**2 + 0.5000000001) / 10**2
    print(y,end='\t')

结果为：

1.38 1.48 3.26 1.13 1.25 3.25 3.26

所有测试的浮点数第3位为5的都进上去了，只要小数第3位及以后位略小于5就舍去，小数第3位及以后位为5或略大于5的就进上。而浮点数的精度产生的误差则不影响结果，完全实现了“四舍五入”数值修约规则。

关于Python的保留小数问题的探讨——实现真正的“四舍五入”数值修约规则

悦读