leetCode刷题记录2

文章目录

hot100题

560. 和为 K 的子数组

先暴力，过了再说

public int subarraySum(int[] nums, int k) {
    int ans = 0;
    for (int i = 0; i < nums.length; i++) {
        int sum = 0;
        for (int j = i; j < nums.length; j++) {
            sum += nums[j];
            if(sum==k) ans++;
        }
    }
    return ans;
}

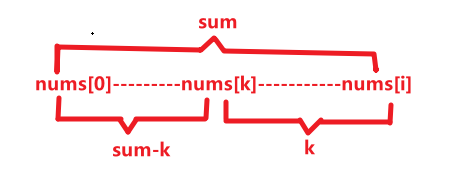
想想之前遍历树时遇到过这个问题，当时用前缀和+Map做得，飞快呀，这里不也可以么

在这里插入图片描述

果然可以，快了不是一点点啊

public int subarraySum(int[] nums, int k) {
    HashMap<Integer, Integer> hash = new HashMap<>();
    hash.put(0,1);//初始化 很重要
    int ans = 0,sum=0;
    for (int i = 0; i < nums.length; i++) {
        sum += nums[i];
        ans += hash.getOrDefault(sum-k,0);// root-A-current   root~current=sum   root~A=sum-k 那么 A~current一定是k
        hash.put(sum,hash.getOrDefault(sum,0)+1);
    }
    return ans;
}

这么写，会快2~3ms

public int subarraySum(int[] nums, int k) {
    HashMap<Integer, Integer> hash = new HashMap<>();
    hash.put(0,1);//初始化 很重要
    int ans = 0,sum=0;
    for (int num : nums) {
        sum += num;
        if(hash.containsKey(sum-k))  ans += hash.get(sum - k);
        if(hash.containsKey(sum)){
            hash.put(sum,hash.get(sum)+1);
        }else {
            hash.put(sum,1);
        }
    }
    return ans;
}

581. 最短无序连续子数组 ▲

581. 最短无序连续子数组

老规矩，先暴力通过再说

public int findUnsortedSubarray(int[] nums) {
    int l=-1,r=-1;
    for (int i = 0; i < nums.length; i++) {
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[j] < nums[i]){//正序遍历 第一个不满足升序的
                l = i;
                break;
            }
        }
        if(l!=-1) break;
    }

    for (int i = nums.length - 1; i >= 0; i--) {
        for (int j = i-1; j >= 0; j--) {
            if (nums[j] > nums[i]){//逆序遍历 第一个不满足降序的
                r = i;
                break;
            }
        }
        if(r!=-1) break;
    }
    return l<r?r-l+1:0;
}

或者排序后比较前最长前缀和最长后缀

public int findUnsortedSubarray(int[] nums) {
    HashMap<Integer, Integer> map = new HashMap<>();
    int[] sort = Arrays.copyOf(nums, nums.length);
    Arrays.sort(sort);
    int l=0,r=nums.length-1;
    while (l<nums.length&&nums[l]==sort[l]) l++;
    while (r>0&&nums[r]==sort[r]) r--;
    return l<r?r-l+1:0;
}

竟然才7ms,也挺快的呀

方法1想法不错但其实实现没那么麻烦

left应该小于右边所有元素为何非要从前往后遍历呢，从后往前遍历其实一趟就够了呀
同样right是后面都比它大也可以从前往后一趟遍历

在这里插入图片描述

public int findUnsortedSubarray(int[] nums) {
    // 想法不错 但其实实现没那么麻烦
    // left应该小于右边所有元素 为何非要从前往后遍历呢，从后往前遍历 其实一趟就够了呀
    int min = Integer.MAX_VALUE, minI = -1;
    for (int i = nums.length-1; i >= 0; i--) {
        if(nums[i]>min) {
            minI=i;
        }else {
            min = nums[i];
        }
    }

    // 同样right是后面都比它大 也可以从前往后一趟遍历
    int max = Integer.MIN_VALUE, maxI=-2;
    for (int i = 0; i < nums.length; i++) {
        if(nums[i]<max) {
            maxI = i;
        }else {
            max = nums[i];
        }
    }

    return minI<maxI?maxI-minI+1:0;
}

当然两次遍历可以优化为1次遍历

public int findUnsortedSubarray(int[] nums) {
    // 想法不错 但其实实现没那么麻烦
    // left应该小于右边所有元素 为何非要从前往后遍历呢，从后往前遍历 其实一趟就够了呀   right也是
    int min = Integer.MAX_VALUE, minI = -1;
    int max = Integer.MIN_VALUE, maxI = -2;
    int n = nums.length;
    for (int i = n - 1; i >= 0; i--) {
        if (nums[i] > min) minI = i;
        else min = nums[i];

        if (nums[n - 1 - i] < max) maxI = n - 1 - i;
        else max = nums[n - 1 - i];
    }
    return minI < maxI ? maxI - minI + 1 : 0;
}

617. 合并二叉树

同步遍历，但是得先验证，后验的话root=null->root=new TreeNode() 连不起来

0ms 时间效率还不错

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
    if(root1==null) return root2;
    if(root2==null) return root1;//开始根就为null的特判

    root1.val += root2.val;

    //System.out.printf("(%d %d)", root1 == null ? -1 : root1.val, root2 == null ? -1 : root2.val);

    if (root1.left != null || root2.left != null) {
        if (root1.left == null) root1.left = new TreeNode(0);
        else if (root2.left == null) root2.left = new TreeNode(0);
        mergeTrees(root1.left, root2.left);
    }

    if (root1.right != null || root2.right != null) {
        if (root1.right == null) root1.right = new TreeNode(0);
        else if (root2.right == null) root2.right = new TreeNode(0);
        mergeTrees(root1.right, root2.right);
    }

    return root1;
}

其实宏观层面看递归，巧用返回值，代码非常优美

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
    if(root1==null) return root2;
    if(root2==null) return root1;

    TreeNode merge = new TreeNode(root1.val+root2.val);
    merge.left = mergeTrees(root1.left,root2.left);
    merge.right = mergeTrees(root1.right,root2.right);

    return merge;
}

621. 任务调度器

模拟失败了，还是慢慢分析吧，这个题解很好，一下就分析清楚了
感觉这一题还是很有难度的，主要太灵活了，得慢慢分析其特性，瞎想不行，得画图建模分析才行

https://leetcode.cn/problems/task-scheduler/solution/tong-zi-by-popopop/

// 多体并行，低位交叉  n+1其实就是并行数目 也是必须间隔的数量  A B C A  两个A之间的下标恰好间隔 n+1
// 最多的那个执行完了 其他的肯定也执行完了 (可以填充啊)
// 当n很小 任务种类很多  种类多直接不用wait了，随意填充就行了 答案就是size

public int leastInterval(char[] tasks, int n) {
    // 多体并行，低位交叉  n+1其实就是并行数目 也是必须间隔的数量  A B C A  两个A之间的下标恰好间隔 n+1
    // 最多的那个执行完了 其他的肯定也执行完了 (可以填充啊)
    // 当n很小 任务种类很多  种类多直接不用wait了，随意填充就行了 答案就是size

    HashMap<Character, Integer> map = new HashMap<>();
    int max = 0;
    for (char c : tasks) {
        int t = map.getOrDefault(c,0)+1;
        map.put(c,t);
        max = Math.max(max,t);
    }

    int N = 0;
    for (char c: map.keySet()) {
        if(map.get(c)==max) N++;
    }

    return Math.max((max-1)*(n+1)+N,tasks.length);
}

优化一下:

public int leastInterval(char[] tasks, int n) {

    int[] hash = new int[26];
    int max = 0;
    for (char c : tasks) {
        hash[c - 'A']++;
        max = Math.max(max, hash[c - 'A']);
    }

    int N = 0;
    for (int i : hash) {
        if (i == max) N++;
    }

    return Math.max((max - 1) * (n + 1) + N, tasks.length);
}

647. 回文子串

dp过了就算了

public int countSubstrings(String s) {
    char[] arr = s.toCharArray();
    int n = arr.length;

    int[][] dp = new int[n][n];
    for (int i = 0; i < n; i++){
        dp[i][i] = 1;
        if(i+1<n&&arr[i]==arr[i+1]) dp[i][i+1]=1; //这也是边界
    }

    // 注意这里是枚举长度
    for (int len = 2; len < n; len++) {
        for (int i = 0; i < n; i++) {
            int j = i+len;
            if (j<n&&arr[i] == arr[j]) {
                dp[i][j] = dp[i + 1][j - 1];
            }
        }
    }
    //HzaUtils.print2DimIntArr(dp);
    int ans = 0;
    for (int i = 0; i < n; i++) {
        for (int j = i; j < n; j++) {
            ans += dp[i][j];
        }
    }
    return ans;
}

有时间优化一下

739. 每日温度

想不出好方法，先暴力吧

果然超时了

想办法优化呀

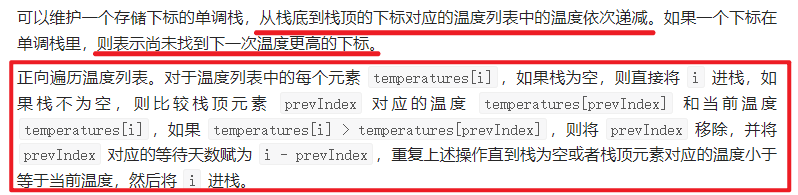
看题解吧，题解的暴力法，感觉也不怎么暴力呀，很巧妙地用到了Hash，具体思路看注释吧

public int[] dailyTemperatures(int[] temp) {
    int[] ans = new int[temp.length];
    int[] next = new int[101]; //30~100 每个温度第一次出现的下标 (倒过来存储Hash就行了)
    Arrays.fill(next,Integer.MAX_VALUE);
    for (int i = temp.length-1; i >=0 ; i--) {
        int min = Integer.MAX_VALUE;
        for (int j = temp[i]+1; j <= 100; j++) {
            min = Math.min(min,next[j]);//比自己写if要快  API似乎被优化了
        }// 温度值比我大 且在我后面的最大下标
        ans[i] = min==Integer.MAX_VALUE?0:min-i;
        // 不能提前遍历好 只能遍历这么多(当前next只记录我后面每个温度第一次出现的下标)
        next[temp[i]] = i;//关键在于边找边建立Hash,这一样倒过来遍历，每次Hash就都只记录了我后面的温度 前面比我大的还不存在，就不会影响到我了
    }
    return ans;
}

看题解，发现了单调栈，真的好用啊

在这里插入图片描述

public int[] dailyTemperatures(int[] temp) {
    int[] ans = new int[temp.length];
    Stack<Integer> st = new Stack();

    st.push(0);
    for (int i = 1; i < temp.length; i++) {
        if(st.isEmpty()||temp[i]<=temp[st.peek()]) st.push(i);
        else {
            while (!st.isEmpty()){
                Integer top = st.peek(); //万一更大呢? 就不能pop了
                if(temp[top]>=temp[i]) break;
                ans[top] = i-top;
                st.pop();
                //System.out.println(top+"："+ans[top]);
            }
            st.push(i);
        }
    }
    // 剩下的直接默认0就行了
    return ans;
}

不错的思路，但是好慢啊，优化一下：

public int[] dailyTemperatures(int[] temp) {
    int[] ans = new int[temp.length];
    Stack<Integer> st = new Stack();

    st.push(0);
    for (int i = 1; i < temp.length; i++) {
        while (!st.isEmpty() && temp[i] > temp[st.peek()]) {
            Integer top = st.pop(); //万一更大呢? 就不能pop了
            ans[top] = i - top;
            //System.out.println(top+"："+ans[top]);
        }
        st.push(i);//其他情况直接入栈就行了 不用多想
    }
    // 剩下的直接默认0就行了
    return ans;
}

还是好慢，用Deque<Integer> st = new LinkedList<>(); 代替 Stack<Integer> st = new Stack(); 快了好多

public int[] dailyTemperatures(int[] temp) {
    int[] ans = new int[temp.length];
    Deque<Integer> st = new LinkedList<>();

    st.push(0);
    for (int i = 1; i < temp.length; i++) {
        while (!st.isEmpty() && temp[i] > temp[st.peek()]) {
            Integer top = st.pop(); //万一更大呢? 就不能pop了
            ans[top] = i - top;
            //System.out.println(top+"："+ans[top]);
        }
        st.push(i);//其他情况直接入栈就行了 不用多想
    }
    // 剩下的直接默认0就行了
    return ans;
}

在这里插入图片描述

可以使用Deuqe代替栈
Deuqe既可以做队列，也可以做栈，而且做栈比Stack快多了，Stack继承自Vector，大量synchronized锁保证了线程安全，但是效率极低

顺便再做两个单调栈的题目吧，好好巩固一下

42. 接雨水

84. 柱状图中最大的矩形

难题补充

72. 编辑距离

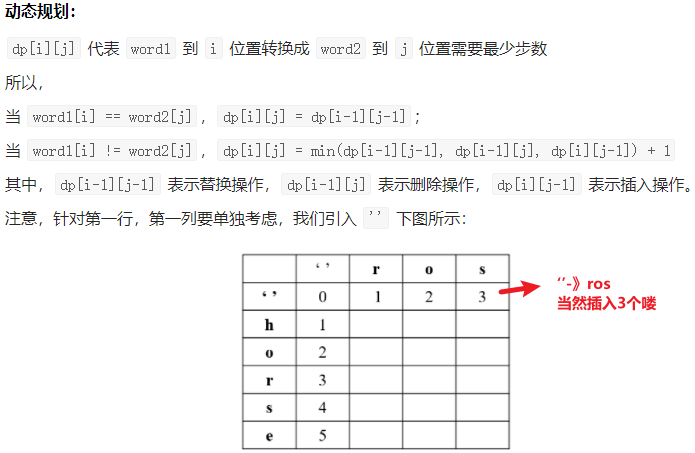
之所以困难主要是dp难想，看懂其实不难

在这里插入图片描述

public int minDistance(String word1, String word2) {
    int ans = 0;

    int m = word1.length(), n = word2.length();
    int[][] dp = new int[m+1][n+1];//dp[i][j]表示前word1前i个子串 转换为 word2前j个子串 需要的最少步数
    // 不定义i为下标i的好处 反而以dp[0][0]表示两个空串(默认0正确)  好处: 边界的初始化很简单  空串不用特判
    for (int i = 1; i <= m; i++)  dp[i][0] = dp[i - 1][0]+1;
    for (int i = 1; i <= n; i++) dp[0][i] = dp[0][i - 1]+1;

    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (word1.charAt(i-1) == word2.charAt(j-1)) dp[i][j] = dp[i-1][j-1];
            else {
                dp[i][j] = Math.min(dp[i-1][j-1],Math.min(dp[i][j-1],dp[i-1][j]))+1;
            }
        }
    }

    //HzaUtils.print2DimIntArr(dp);

    return dp[m][n];
}

要是不填充空，也就是0表示下标0而不是空，代码会麻烦许多，特判+初始化都麻烦

public int minDistance(String word1, String word2) {
    if(word1.length()==0||word2.length()==0){
        if(word1.equals(word2)) return 0;
        return Math.max(word1.length(),word2.length());
    }

    int ans = 0;

    int m = word1.length(), n = word2.length();
    int[][] dp = new int[m][n];//dp[i][j]表示前word1[0~i] 转换为 word2[0~j] 需要的最少步数
    
    // dp[0][0] 就表示 两个下标0元素进行比较时 初始化会比较麻烦  所以填充一个空 对初始化友好多了
    boolean flag = false;
    for (int i = 0; i < m; i++) {
        if(word1.charAt(i)==word2.charAt(0)) flag = true;//无论中间哪里 有一个相等 就少一次
        dp[i][0] = flag?i:i+1;
    }
    flag = false;
    for (int i = 0; i < n; i++) {
        if(word1.charAt(0)==word2.charAt(i)) flag = true;
        dp[0][i] = flag?i:i+1;
    }

    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            if (word1.charAt(i) == word2.charAt(j)) dp[i][j] = dp[i-1][j-1];
            else {
                dp[i][j] = Math.min(dp[i-1][j-1],Math.min(dp[i][j-1],dp[i-1][j]))+1;
            }
        }
    }
    //HzaUtils.print2DimIntArr(dp);
    return dp[m-1][n-1];
}

1071. 字符串的最大公因子

核心点:
1、若存在非空最大公因子串，则其长度一定是两个串长度的最大公因数
2、若存在非空最大公因子串，则短串一定是长串的前缀

根据这两点可以写出不错的解法了：

public String gcdOfStrings(String str1, String str2) {
    if (str1.length() < str2.length()) {
        String t = str1;
        str1 = str2;
        str2 = t;
    }

    int n1 = str1.length(), n2 = str2.length();

    if (!str1.startsWith(str2)) return "";//短的必然是长的前缀

    int k = gcd(n1, n2);//二者最大公约数 的长度是最终答案 但是内容满不满足还得验证
    String base = str2.substring(0, k);
    for (int i = 0; i < n1; i += k) {
        if (!str1.substring(i, i + k).equals(base)) return "";
    }
    return base;

}

public int gcd(int a, int b) {
    if (b == 0) return a;
    return gcd(b, a % b);
}

但其实第二点可以换成一个更好的第二点
核心点:
1、若存在非空最大公因子串，则其长度一定是两个串长度的最大公因数
2、若存在非空最大公因子串，则 “串1+串2”==“串2+串1” 而且是充要条件 (都是公因子串拼成的嘛)

根据这两点，可以写出极简代码

 /*public String gcdOfStrings(String str1, String str2) {
     if(!(str1+str2).equals(str2+str1)) return "";
     return str1.substring(0,gcd(str1.length(),str2.length()));
 }*/

 public String gcdOfStrings(String str1, String str2) {
     if (!(str1.concat(str2)).equals(str2.concat(str1))) return "";//用API会快一点点
     return str1.substring(0, gcd(str1.length(), str2.length()));
 }

 public int gcd(int a, int b) {
     if (b == 0) return a;
     return gcd(b, a % b);
 }

面试精华75题

334. 递增的三元子序列

按照最长递增子序列来做，O(n^2)会超时

以中间一个元素为基准，两次遍历O(n)

// 左边有比我小的  右边有比我大的就行
public boolean increasingTriplet(int[] nums) {
    boolean[] leftHashSmall = new boolean[nums.length];

    int min = nums[0];
    for (int i = 1; i < nums.length; i++) {
        if(nums[i]>min) leftHashSmall[i]=true;
        else if(nums[i]<min) min = nums[i];
    }

    int max = nums[nums.length-1];
    for (int i = nums.length-2; i >= 0; i--) {
        if(nums[i]<max){//右边有比我大的
            if(leftHashSmall[i]) return true;//左边有比我小的
        }else if(nums[i]>max) max = nums[i];
    }
    return false;
}

直接贪心first和second

贪心(维护)最小的前两个数a，b (a<b). 然后找>b的c即可，途中维护最小的a,b

贪心好厉害

// l一次遍历 贪心(维护)最小的前两个数
public boolean increasingTriplet(int[] nums) {
    int a=nums[0],b=Integer.MAX_VALUE;
    for (int i = 1; i < nums.length; i++) {
        if(nums[i]>b) return true;
        else if(nums[i]>a) b = nums[i];
        else a = nums[i];//维护最小的a和b 这样组合成递增三元组的概率最大
    }
    return false;
}

443. 压缩字符串

真的不难，但是代码好复杂

public int compress(char[] chars) {
    int n = 0, k = 1;
    char base = chars[0];
    if(chars.length==1) return 1;
    for (int i = 1; i < chars.length; i++) {
        if (chars[i] == base) k++;
        else{
            chars[n++] = base;
            if (k > 1) {
                String st = String.valueOf(k);
                for (int j = 0; j < st.length(); j++) {
                    chars[n++] = st.charAt(j);
                }
            }
            k = 1;
            base = chars[i];
        }
    }

    // 最后一个比较复杂 必须特判 (像a,b,c这种情况 最后一个真的就只有特殊处理了)
    chars[n++] = base;
    if (k > 1) {
        String st = String.valueOf(k);
        for (int j = 0; j < st.length(); j++) {
            chars[n++] = st.charAt(j);
        }
    }

    System.out.println(chars);
    return n;
}

看题解，简化了下代码，好看多了;

public int compress(char[] chars) {
    int n = chars.length;
    int write=0,start=0;

    for (int read = 0; read < n; read++) {//实际判断的是read+1 方便边界处理
        if(read==n-1||chars[read+1]!=chars[start]){
            chars[write++]=chars[start];
            int len = read - start + 1;
            if(len>1){
                String st = String.valueOf(len);
                for (int i = 0; i < st.length(); i++) {
                    chars[write++] = st.charAt(i);
                }
            }
            start = read+1;
        }
    }
    System.out.println(Arrays.copyOf(chars,write));
    return write;
}

1679. K 和数对的最大数目

先用hash做

public int maxOperations(int[] nums, int k) {
    HashMap<Integer, Integer> hash = new HashMap<Integer,Integer>();
    int ans = 0;
    for (int i = 0; i < nums.length; i++) {
        if(hash.containsKey(k-nums[i])){
            if(hash.get(k-nums[i])==1) hash.remove(k-nums[i]);
            else hash.put(k-nums[i], hash.get(k-nums[i])-1);
            //System.out.println(i+":\t"+nums[i]+"\t"+(k-nums[i]));
            ans++;
        }else {
            hash.put(nums[i], hash.getOrDefault(nums[i],0)+1);
        }
    }
    return ans;
}

好慢，改用排序做，反而很快

// 直接排序反而要更快
public int maxOperations(int[] nums, int k) {
    Arrays.sort(nums);
    int i=0;
    int j=nums.length-1;
    int ans = 0;
    while (i<j){
        int sum = nums[i]+nums[j];
        if(sum<k) i++;
        else if(sum>k) j--;
        else {
            ans++;
            i++;j--;
        }
    }
    return ans;
}

1004. 最大连续1的个数 III

1004. 最大连续1的个数 III
知道是滑动窗口就没啥难度了

public int longestOnes(int[] nums, int k) {
    int ans = -1;
    int count = 0;
    int l = 0;

    for (int r = 0; r < nums.length; r++) {//r是终点  l是起点
        if(nums[r]==0) count++;
        while (count>k){
            while (nums[l]==1) l++;
            count--;l++;
        }
        ans = Math.max(ans,r-l+1);
    }
    return ans;
}

1493. 删掉一个元素以后全为 1 的最长子数组

和上一题一样，滑动窗口，很简单

public int longestSubarray(int[] nums) {
    int ans = 0;
    int l = 0;
    int zero = 0;
    for (int r = 0; r < nums.length; r++) {
        if (nums[r] == 0) zero++;
        if (zero > 1) {//中间可以有0个或者1个0
            while (nums[l] == 1) l++;
            l++;zero--;
        }
        ans = Math.max(ans, r - l + 1 - zero);
    }
    return ans==nums.length?ans-1:ans;//至少删掉一个
}

1657. 确定两个字符串是否接近

// 元素个数组成的集合一样就能转
// 元素种类数也得一样
public boolean closeStrings(String word1, String word2) {
    int n1 = word1.length(), n2 = word2.length();
    if (n1 != n2) return false;
    int[] count1 = new int[26];
    int[] count2 = new int[26];
    for (int i = 0; i < n1; i++) {
        count1[word1.charAt(i) - 'a']++;
        count2[word2.charAt(i) - 'a']++;
    }

    // 元素只能互换，因此出现的元素种类数必须一样，只是数量可以不一样
    for (int i = 0; i < 26; i++) {
        if (count1[i] == 0 && count2[i] != 0) return false;
        if (count2[i] == 0 && count1[i] != 0) return false;
    }

    // 26个数字 排序一下 时间复杂度忽略不计
    Arrays.sort(count1);
    Arrays.sort(count2);
    for (int i = 0; i < 26; i++) {
        if (count1[i] != count2[i]) return false;
    }
    return true;
}

2352. 相等行列对

编码+hash

public int equalPairs(int[][] grid) {
    int n = grid.length;

    HashMap<String, Integer> map1 = new HashMap<>();
    for (int i = 0; i < n; i++) {
        String s = "";
        for (int j = 0; j < n; j++) {
            s += grid[i][j]+"-";
        }
        map1.put(s,map1.getOrDefault(s,0)+1);
    }

    HashMap<String, Integer> map2 = new HashMap<>();
    for (int i = 0; i < n; i++) {
        String s = "";
        for (int j = 0; j < n; j++) {
            s += grid[j][i]+"-";
        }
        map2.put(s,map2.getOrDefault(s,0)+1);
    }

    //System.out.println(map1);
    //System.out.println(map2);
    int ans = 0;
    for (String key : map1.keySet()) {
        if(map2.containsKey(key)){
            ans += map1.get(key)*map2.get(key);
        }
    }
    return ans;
}

其实不需要编码，直接list就可以作为key

public int equalPairs(int[][] grid) {
    int n = grid.length;

    HashMap<List<Integer>, Integer> map = new HashMap<>();
    for (int i = 0; i < n; i++) {
        ArrayList<Integer> list = new ArrayList<>();
        for (int j = 0; j < n; j++) {
            list.add(grid[i][j]);
        }
        map.put(list,map.getOrDefault(list,0)+1);
    }
    //print(map);

    int ans = 0; // 第二就可以计算结果了
    for (int i = 0; i < n; i++) {
        ArrayList<Integer> list = new ArrayList<>();
        for (int j = 0; j < n; j++) {
            list.add(grid[j][i]);
        }
        ans += map.getOrDefault(list,0);
    }
    return ans;
}

2390. 从字符串中移除星号

提示是栈就很简单了，但是用栈速度很慢

public String removeStars(String s) {
    // 双端队列
    Deque<Character> st = new LinkedList<>();
    // 先当作栈来用
    for (int i = 0; i < s.length(); i++) {
        if(s.charAt(i)=='*') st.pop();
        else st.push(s.charAt(i));
    }
    // 再当作队列来取出元素
    String ans = "";
    while (!st.isEmpty()){
        ans += st.pollLast();
    }
    return ans;
}

不如直接用数组模拟栈，快多了

public String removeStars(String s) {
    char[] ans = new char[s.length()];
    int k = 0;
    for (int i = 0; i < s.length(); i++) {
        if(s.charAt(i)=='*') k--;
        else ans[k++]=s.charAt(i);
    }
    return String.copyValueOf(ans,0,k);
}

735. 行星碰撞

数组模拟栈

// 数组模拟栈 每次入栈和栈顶符号不同则碰撞
public int[] asteroidCollision(int[] asteroids) {
    int[] ans = new int[asteroids.length];
    int k = 0;
    for (int i = 0; i < asteroids.length; i++) {
        if(k==0){
            ans[k++] = asteroids[i];//要么第一个 要么向左都撞没了
            continue;
        }

        if(ans[k-1]<0||asteroids[i]>0) ans[k++] = asteroids[i];//撞不上(前面的往前，后面的往后)
        else if(asteroids[i]==-ans[k-1]){
            k--;//两败俱伤
        }else if(Math.abs(asteroids[i])>Math.abs(ans[k-1])){
            k--;// 栈顶被撞死了
            i--;//接着撞
            //(要么自己被撞死 要么撞死别人 要么两拜俱伤 要么撞没了)
        }else {
            // Math.abs(asteroids[i])<Math.abs(ans[k-1]) // 啥也不用干 直接忽略 i++即可 asteroids[i]被撞死了
        }
    }

    return Arrays.copyOf(ans,k);
}

语法层面优化

// 数组模拟栈 每次入栈和栈顶符号不同则碰撞
public int[] asteroidCollision(int[] asteroids) {
    int[] ans = new int[asteroids.length];
    int k = 0;
    for (int i = 0; i < asteroids.length; i++) {
        if(k==0){
            ans[k++] = asteroids[i];//要么第一个 要么向左都撞没了
            continue;
        }
        if(ans[k-1]<0||asteroids[i]>0) ans[k++] = asteroids[i];//撞不上(前面的往前，后面的往后)
        else if(asteroids[i]==-ans[k-1]) k--;//两败俱伤
        else if(Math.abs(asteroids[i])>Math.abs(ans[k-1])){
            k--;//栈顶被撞死了
            i--;//此个接着撞
        }
    }
    return Arrays.copyOf(ans,k);
}

649. Dota2 参议院

自己手动模拟禁用过程，82个用例都能过，但是超时了：

public char opp(char c){
    if(c=='R') return 'D';
    return 'R';
}

public String predictPartyVictory(String senate) {
    int n = senate.length();
    char[] sen = senate.toCharArray();
    boolean[] died = new boolean[n];

    while (true){
        int sr=0,sd=0;
        for (int i = 0; i < sen.length; i++) {
            if(!died[i]){
                int j=(i+1)%n;
                while (j!=i) {//找了一圈还没找到 放弃吧
                    if(!died[j]&&sen[j]==opp(sen[i])) {
                        died[j]=true;
                        break;
                    }
                    j = (j+1)%n;//循环消灭他人
                }
                if(sen[i]=='R') sr++;
                else sd++;
            }
        }

        if(sr==0) return "Dire";
        if(sd==0) return "Radiant";
    }
}

看了题解，果然好多了，直接用两个队列，减少了每次查下一个最早投票的对方选手的时间
先两个队列分别存储双方选手(实际存储发言时间)
每次比较队头数字大小，谁小谁先发言
本选手发言后去掉一个对方队头选手，然后本选手(发言时间+n)放到队尾部
哪个队列先空，就负

public String predictPartyVictory(String senate) {
     Queue<Integer> qR = new LinkedList<>();
     Queue<Integer> qD = new LinkedList<>();

     for (int i = 0; i < senate.length(); i++) {
         if(senate.charAt(i) =='R') qR.offer(i);
         else qD.offer(i);
     }

     while (true){
         if(qR.isEmpty()) return "Dire";
         if(qD.isEmpty()) return "Radiant";

         if(qR.peek()<qD.peek()){//注意getLast是拿最先进入队列的
             qD.poll();//去掉队头 反过来了
             Integer first = qR.poll();
             qR.offer(first+senate.length());//队头+n移到队尾部 以便进行下一轮发言
         }else {
             qR.poll();
             Integer first = qD.poll();
             qD.offer(first + senate.length());
         }
     }
 }

但是我的代码写得太渣了优化一下

public String predictPartyVictory(String senate) {
    Queue<Integer> qR = new LinkedList<>();
    Queue<Integer> qD = new LinkedList<>();
    for (int i = 0; i < senate.length(); i++) {
        if (senate.charAt(i) == 'R') qR.offer(i);
        else qD.offer(i);
    }
    while (true) {
        if (qR.isEmpty()) return "Dire";
        if (qD.isEmpty()) return "Radiant";
        int r = qR.poll(), d = qD.poll();
        if(r<d){
            qR.offer(r+senate.length());
        }else {
            qD.offer(d+senate.length());
        }
    }
}

Queue<Integer> qR = new LinkedList<>(); 队列用Queue
Deque<Integer> qD = new LinkedList<>(); 栈用Deque

2095. 删除链表的中间节点

双指针法，找中间节点前驱
不同于找中间节点，快指针要提前多走一次才行

public ListNode deleteMiddle(ListNode head) {
     if(head.next==null) return null;//只有一个节点
     ListNode p = head, q = head.next.next;
     while (q != null) {
         q = q.next;
         if (q == null) break;
         q = q.next;
         p = p.next;
     }
     p.next = p.next.next;
     return head;
 }

328. 奇偶链表

这题做中等也太水了吧

public ListNode oddEvenList(ListNode head) {
    if(head==null||head.next==null) return head;
    ListNode odd = head, even = head.next;
    ListNode tailOld = odd, tailEven = even;
    ListNode p = head.next.next;
    while (p != null) {
        tailOld.next = p;
        tailOld = p;

        if (p == null || p.next == null) break;
        p = p.next;
        tailEven.next = p;
        tailEven = p;
        p = p.next;
    }
    tailOld.next = even;
    tailEven.next = null;
    return odd;
}

2130. 链表最大孪生和

个人感觉很简单，就是双指针找中点，然后，头插法逆置链表
但是我的代码感觉写得很烂

// 链表后半段 逆置即可
public int pairSum(ListNode head) {
    int ans = 0;

    ListNode p = head,q=head;
    while (q!=null){
        p = p.next;
        q = q.next;
        if(q==null) break;
        q = q.next;
    }

    // 现在 p是中点了 需要对p进行逆置了
    ListNode ph = null; // 先开一个空链表
    while (p!=null){
        q = p.next;

        // 头插法逆置
        p.next = ph;
        ph = p;

        p = q;
    }

    //head.show();
    //ph.show();

    q = head;
    p = ph;
    while (p!=null){
        ans = Math.max(ans,p.val+q.val);
        p = p.next;
        q = q.next;
    }

    return ans;
}

Tip1: list1.equals(list2)

可以直接比较两个list打印输出是否一样（对应元素是否完全相同）

1372. 二叉树中的最长交错路径 (值得2刷)

1372. 二叉树中的最长交错路径

// 起点也要遍历
int ans = 1;
public int longestZigZag(TreeNode root) {
    if (root == null)  return 0;
    ans = Math.max(ans,Math.max(longest(root,-1),longest(root,1)));
    longestZigZag(root.left);
    longestZigZag(root.right);
    return ans-1;
}

public int longest(TreeNode root,int direct) {//-1左 1右
    if(root == null) return 0;
    if(direct==-1) return 1+longest(root.left,-direct);
    else return 1+longest(root.right,-direct);
}

太暴力了超时了

给longest递归加上缓存

加上缓存能过了，但是代码好乱

// 选哪个作为起点也要遍历
int ans = 1;
public int longestZigZag(TreeNode root) {
    if (root == null)  return 0;
    ans = Math.max(ans,Math.max(longest(root,0),longest(root,1)));
    longestZigZag(root.left);
    longestZigZag(root.right);
    return ans-1;
}

// 超时 做下缓存 又称：记忆化搜索
HashMap<TreeNode, int[]> cache = new HashMap<>();
public int longest(TreeNode root,int direct) {//0左 1右
    if(root == null) return 0;
    if(cache.containsKey(root)){
        if(cache.get(root)[direct]>0)
            return cache.get(root)[direct];
    }
    int[] ans = new int[2];
    if(direct==0) {
        ans[0] = 1+longest(root.left,1);
        if(cache.containsKey(root)) ans[1]=cache.get(root)[1];
        cache.put(root,ans);
        return ans[0];
    }else {
        ans[1] = 1+longest(root.right,0);
        if(cache.containsKey(root)) ans[0]=cache.get(root)[0];
        cache.put(root,ans);
        return ans[1];
    }
}

可以理解为一种简单的树形dp吧

199. 二叉树的右视图

刚开始觉得很难，直接回去睡觉了，出去完了两天，罪恶感满满，回来继续刷，真简单，NRL地遍历，遍历到每层的第一个就是答案

// 第一思路: NRL地遍历，每层第一个即是
public List<Integer> rightSideView(TreeNode root) {
    ArrayList<Integer> ans = new ArrayList<>();
    dfs(root,0,ans);
    return ans;
}
void dfs(TreeNode root,int layer,List<Integer> ans){
    if(root==null) return;
    if(ans.size()==layer) ans.add(root.val);
    dfs(root.right,layer+1,ans);
    dfs(root.left,layer+1,ans);
}

代码优化：

// 第一思路: NRL地遍历，每层第一个即是
public List<Integer> rightSideView(TreeNode root) {
    return dfs(root,0,new ArrayList<>());
}
List<Integer> dfs(TreeNode root,int layer,List<Integer> ans){
    if(root==null) return ans;
    if(ans.size()==layer) ans.add(root.val);
    dfs(root.right,layer+1,ans);
    dfs(root.left,layer+1,ans);
    return ans;
}

1161. 最大层内元素和

BFS求每层元素和而已

// BFS比较好
public int maxLevelSum(TreeNode root) {
    int[] ans = {0,Integer.MIN_VALUE};//层号+数量
    if(root==null) return 0;

    Queue<TreeNode> q = new LinkedList<TreeNode>();
    q.add(root);
    int layer=0;
    while (!q.isEmpty()){
        layer++;
        int T = q.size();
        int t = 0;
        while (T-->0){
            TreeNode top = q.poll();
            t += top.val;
            if(top.left!=null) q.offer(top.left);
            if(top.right!=null) q.offer(top.right);
        }
        if(t>ans[1]){
            ans[1]=t;
            ans[0]=layer;
        }
    }
    return ans[0];
}

450. 删除二叉搜索树中的节点

BST的删除，太经典了，就不觉得难了。【AVL和RBT的删除才是难】

// 经典BST的删除 【还好,AVL和RBT的删除才是难，要旋转】
public TreeNode deleteNode(TreeNode root, int key) {
    if (root == null) return null;
    if (root.val == key) {
        if (root.left == null && root.right == null) return null;
        else if (root.left != null && root.right != null) {
            // 找到右子树最左的结点替代我
            TreeNode node = root.right;
            while (node.left!=null) node = node.left;
            root.val = node.val;
            // 替代后递归在右子树中删除刚刚替代的结点 这一次一定是简单情况 大胆递归调用
            root.right = deleteNode(root.right,node.val);
            return root;
        } else if (root.left != null) return root.left;
        else return root.right;//return是为了赋值给下面两个分支的赋值语句 避免了值传递的尴尬
    } else if (key < root.val) {
        root.left = deleteNode(root.left, key);//赋值操作 保证了更新 也不需要获取每个节点的父引用了
    } else {
        root.right = deleteNode(root.right, key);
    }
    return root;
}

841. 钥匙和房间

// 就是建图 然后看从0号结点开始能不能遍历完图
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
    // 先记录下有多少个结点
    HashMap<Integer, Boolean> visit = new HashMap<>();
    for (List<Integer> room : rooms) {
        for (Integer i : room) {
            visit.put(i, false);
        }
    }
    dfs(rooms,0,visit);
    for (Boolean value : visit.values()) {
        if(value==false) return false;//还有没有被访问到的
    }
    return true;
}

private void dfs(List<List<Integer>> rooms,int k,HashMap<Integer, Boolean> visit){
    visit.put(k,true);
    for (Integer i : rooms.get(k)) {
        if(!visit.get(i)){
            dfs(rooms,i,visit);
        }
    }
}

傻了，其实直接list.size就是总顶点个数，不然为啥会出现[ []]呢

// 就是建图 然后看从0号结点开始能不能遍历完图
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
    // 先记录下有多少个结点
    HashSet<Integer> visited = new HashSet<>();
    dfs(rooms,0,visited);
    return visited.size()== rooms.size();
}

private void dfs(List<List<Integer>> rooms,int k,HashSet<Integer> visited){
    visited.add(k);
    for (Integer i : rooms.get(k)) {
        if(!visited.contains(i)){
            dfs(rooms,i,visited);
        }
    }
}

并查集也能求连通分量个数

// 求无向图连通分量的个数  也就是dfs的次数
public int findCircleNum(int[][] isConnected) {
    int n = isConnected.length;
    int[] Father = new int[n];
    for (int i = 0; i < n; i++) Father[i] = i;//初始每个节点都是一个独立的集合
    for (int i = 0; i < isConnected.length; i++) {
        for (int j = 0; j < isConnected[i].length; j++) {
            if(i!=j&&isConnected[i][j]==1){
                Union(i,j,Father);
            }
        }
    }

    // 现在看看有几个父亲就行了
    HashSet<Integer> set = new HashSet<>();
    for (int i = 0; i < n; i++){
        set.add(findFather(i,Father));
    }

    return set.size();
}

private int findFather(int x,int[] Father){
    int a = x;
    while (x!=Father[x]){
        x = Father[x];
    }
    // 路径压缩
    while (a!=Father[a]){
        int z = a;
        a = Father[a];
        Father[z] = x;
    }
    return x;
}

private void Union(int x,int y,int[] Father){
    int fa = findFather(x,Father);
    int fb = findFather(y,Father);
    if(fa!=fb){
        Father[fa]=fb;
    }
}

1466. 重新规划路线

0开始，DFS一直往前走，遇到未访问过的入边就改为出边即可

(n-1)-修改的入边数 = 最终结果

public int minReorder(int n, int[][] connections) {
    List<List<Integer>> in = new ArrayList<>(n);
    List<List<Integer>> out = new ArrayList<>(n);
    for (int i = 0; i < n; i++) in.add(new ArrayList<>());
    for (int i = 0; i < n; i++) out.add(new ArrayList<>());
    for (int[] conn : connections) {
        out.get(conn[0]).add(conn[1]);
        in.get(conn[1]).add(conn[0]);
    }
    return n-1-dfs(0,in,out,new boolean[n]);
}
private int dfs(int n, List<List<Integer>> in,List<List<Integer>> out,boolean[] visited){
    int ans = 0;
    visited[n] = true;
    // 入边都改成出边
    for (Integer i : in.get(n)) {
        if(!visited[i]){
            ans++;
            out.get(n).add(i);
        }
    }
    // dfs往前走
    for (Integer o : out.get(n)) {
        if(!visited[o]) ans += dfs(o,in,out,visited);
    }
    return ans;
}

399. 除法求值

个人觉得最简单的做法就是并查集了，但是自己写的代码太复杂了，而且调试了很久很久

Map<String, String> Father = new HashMap<>();
Map<String, Map<String, Double>> edge = new HashMap<>();
Set<String> set = new HashSet<>();
//Integer v = edge.get("a").get("b");//a/b=v 权重矩阵

// 个人感觉 这一题 用带权并查集 是最简单的
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
    // 初始化
    for (int i = 0; i < equations.size(); i++) {
        String a = equations.get(i).get(0);
        String b = equations.get(i).get(1);

        set.add(a);//记录有哪些节点
        set.add(b);

        Father.put(a, a);// 初始化每个结点一个集合
        Father.put(b, b);

        if (edge.containsKey(a)) {// 初始化权值
            edge.get(a).put(b, values[i]);
        } else {
            Map<String, Double> map = new HashMap<>();
            map.put(b, values[i]);
            edge.put(a, map);
        }

        if (edge.containsKey(b)) {// 双向初始化权值
            edge.get(b).put(a, 1.0/values[i]);
        } else {
            Map<String, Double> map = new HashMap<>();
            map.put(a, 1.0/values[i]);
            edge.put(b, map);
        }

        edge.get(a).put(a,1.0);
        edge.get(b).put(b,1.0);

    }

    // 合并
    for (int i = 0; i < equations.size(); i++) {
        String a = equations.get(i).get(0);
        String b = equations.get(i).get(1);
        Union(a, b);
    }

    double[] ans = new double[queries.size()];
    // 计算
    for (int i = 0; i < queries.size(); i++) {
        String a = queries.get(i).get(0);
        String b = queries.get(i).get(1);

        if(!set.contains(a)||!set.contains(b)){
            ans[i]=-1.0;
            continue;
        }

        String fa = findFather(a);
        String fb = findFather(b);
        if(fa!=fb) ans[i]=-1.0;
        else {
            double t1 = edge.get(fa).get(a);
            double t2 = edge.get(fb).get(b);//注意此时fa==fb
            ans[i] = t2/t1;
        }
    }
    return ans;
}

private String findFather(String s) {
    String a = s;
    double t = 1.0;
    while (s != Father.get(s)) {
        String f = Father.get(s);
        t*= edge.get(f).get(s);
        edge.get(f).put(a,t);//注意这里写f 因为t已经乘过了
        edge.get(a).put(f,1.0/t);
        s = f;
    }
    // 长度很低 最长20 不需要路径压缩 压缩之后反而不好计算权值了
    return s;
}

private void Union(String a, String b) {
    String fa = findFather(a);
    String fb = findFather(b);
    if (!fa.equals(fb)) {
        double t1 = edge.get(fa).get(a);
        double t2 = edge.get(fb).get(b);
        double t3 = edge.get(a).get(b);
        double v = t1*t3/t2;
        edge.get(fa).put(fb,v);
        edge.get(fb).put(fa,1.0/v);
        Father.put(fb, fa);
    }
}

接下来看题解优化代码：

题解上来就做一个非常好的优化，将String->int 编码之后，并查集代码就和传统的一样简单了
总体比我的代码要简单

后期有时间再修改吧

1926. 迷宫中离入口最近的出口

1、BFS不需要写辅助函数，怎么简单怎么来，java不是c++,很有好的特性使得单个函数更加简单
2、这里BFS不管怎么遍历，标记一个结点是否被访问过一定是入队之后就立刻标记，不能poll时才标记，会导致有些结点重复入队，保证不重复入队的标记才有效果啊！！！！！ 入队时就要变墙，也就是BFS入队时就要标记为已经被访问过了

// 经典走迷宫问题 m,n达到100了，用BFS吧
public int nearestExit(char[][] maze, int[] entrance) {
    int M = maze.length, N = maze[0].length;
    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};

    Queue<int[]> q = new LinkedList<int[]>();
    q.offer(new int[]{entrance[0], entrance[1]});
    maze[entrance[0]][entrance[1]]='+';//入队了就立刻标记 标记的真实作用就是为了避免重复入队

    int layer = 0;
    while (!q.isEmpty()) {
        int T = q.size();
        while (T-- > 0) {
            // 每次先处理一层的 这样写确实好多了
            int[] top = q.poll();
            //maze[top[0]][top[1]] = '+';//入队时就要变墙 否则超时(还是会重复录入) ！！！！
            // 找到出口
            if (layer > 0 && (top[0] == 0 || top[0] == M - 1 || top[1] == 0 || top[1] == N - 1)) return layer;
            // 没找到就入下一层
            for (int i = 0; i < 4; i++) {
                int nx = dx[i] + top[0];
                int ny = dy[i] + top[1];
                if (nx >= 0 && nx < M && ny >= 0 && ny < N && maze[nx][ny] == '.') {
                    q.offer(new int[]{nx, ny});
                    maze[nx][ny]='+';//1、入队时就要变墙!!!!!!!!! 否则超时 会导致有些节点重复入队的	2、避免使用visited数组
                }
            }
        }
        layer++;
    }
    return -1;
}

994. 腐烂的橘子

先自己瞎搞，也能过：
思路就是慢慢扩散，第一次感染的全部改成3，第二次改成4，依次类推

public int orangesRotting(int[][] grid) {
    int ans = 0;

    int M = grid.length;
    int N = grid[0].length;

    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};

    while (true) {
        boolean hasOne = false;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == 1) {
                    hasOne = true;
                    break;
                }
            }
            if (hasOne) break;
        }

        if (!hasOne) return ans;
        if (ans>M*N) return -1;

        int now = 2+ans;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == now) {
                    grid[i][j]++;
                    for (int k = 0; k < 4; k++) {
                        int x = dx[k] + i;
                        int y = dy[k] + j;
                        if (x >= 0 && x < M && y >= 0 && y < N && grid[x][y] == 1) {//只染指旁边新鲜的
                            grid[x][y] = now+1;
                        }
                    }
                }
            }
        }
        ans++;
    }
}

在这里插入图片描述
内存100%，时间上也还行，就2ms

简单优化一下:

public int orangesRotting(int[][] grid) {
    int ans = 0;

    int M = grid.length;
    int N = grid[0].length;

    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};

    int refresh = 0;
    for (int i = 0; i < grid.length; i++) {
        for (int j = 0; j < grid[i].length; j++) {
            if (grid[i][j] == 1) refresh++;
        }
    }

    while (true) {
        if (refresh==0) return ans;
        if (ans>M*N) return -1;
        int now = 2+ans;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == now) {
                    grid[i][j]++;
                    for (int k = 0; k < 4; k++) {
                        int x = dx[k] + i;
                        int y = dy[k] + j;
                        if (x >= 0 && x < M && y >= 0 && y < N && grid[x][y] == 1) {//只染指旁边新鲜的
                            grid[x][y] = now+1;
                            refresh--;
                        }
                    }
                }
            }
        }
        ans++;
    }
}

看了题解才发现没有那么麻烦，直接BFS就行了。就一个不一样的地方: 开始所有的腐烂的2都视为同一层(第0层)

public int orangesRotting(int[][] grid) {
    int M = grid.length,N=grid[0].length;
    int refresh=0;
    Queue<int[]> q = new LinkedList<int[]>();
    for (int i = 0; i < M; i++) {
        for (int j = 0; j < N; j++) {
            if(grid[i][j]==2)  q.offer(new int[]{i,j});
            else if(grid[i][j]==1) refresh++;
        }
    }
    if(refresh==0) return 0;

    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};
    int layer = 0;
    while (!q.isEmpty()){
        int T = q.size();
        while (T-->0){
            int[] top = q.poll();
            for (int i = 0; i < 4; i++) {
                int x = dx[i] + top[0];
                int y = dy[i] + top[1];
                if (x >= 0 && x < M && y >= 0 && y < N && grid[x][y] == 1) {//只染指旁边新鲜的
                    q.offer(new int[]{x,y});
                    grid[x][y] = 2;//立刻标记为腐烂
                    refresh--;
                }
            }
        }
        layer++;
        if(refresh==0) return layer;
    }
    return -1;
}

真的感觉自己算法都学死了，就是BFS呀，为啥搞得这么麻烦呢

2336. 无限集中的最小数字

直接暴力也能通过（因为说了只会调用1000次）直接用个Hash表记录不存在的，然后每次最小的未出现的正整数直接从0开始找就行了，也能过

HashSet<Integer> remove;
public SmallestInfiniteSet() {
    remove = new HashSet<Integer>();
    // 只能记录哪些元素被移除了 也就是不存在
    // 无法维护哪些元素存在
}

public int popSmallest() {
    for (int i = 1; ; i++) {
        if(!remove.contains(i)) {
            remove.add(i);
            return i;//最多只会调用1000次 因此不会很大
        }
    }
}

public void addBack(int num) {
    remove.remove(num);
}

优化1

HashSet<Integer> remove;
int min;

public SmallestInfiniteSet() {
    remove = new HashSet<Integer>();
    min = 1;
    // 只能记录哪些元素被移除了 也就是不存在
    // 无法维护哪些元素存在
}

public int popSmallest() {
    int ans = min;
    remove.add(min);
    min++;
    while (remove.contains(min)) min++;
    return ans;
}

public void addBack(int num) {
    remove.remove(num);
    if(num<min) min=num;
}

看清题意，num，也就是元素值，最大是1000

最强思路：
pop一定按照从小到大pop的所以维护一个min++即可
min的不用管一定没有pop
<min 放在优先队列里优先队列(默认小根堆)不空，则先pop优先队列里的否则 pop min++

最优写法

int min = 1;
PriorityQueue<Integer> pq = new PriorityQueue<>();//默认小根堆
HashSet<Integer> set = new HashSet<Integer>();//完全用来去重的 防止重复往优先队列里add更小的

public SmallestInfiniteSet_3() {

}

public int popSmallest() {
    if (pq.size() == 0) return min++;
    else {
        Integer poll = pq.poll();
        set.remove(poll);//不在优先队列里了
        return poll;
    }
}

public void addBack(int num) {
    if (num < min && set.add(num)) {//set.add(num) 如果已经存在 就会add失败返回false 多好啊
        pq.offer(num);
    }
}

紧扣1000 这么写都行

PriorityQueue<Integer> pq = new PriorityQueue<>();//默认小根堆
HashSet<Integer> set = new HashSet<Integer>();//完全用来去重的 防止重复往优先队列里add更小的

public SmallestInfiniteSet() {
    for (int i = 1; i <= 1000; i++) {
        pq.offer(i);
        set.add(i);
    }
}

public int popSmallest() {
    Integer min = pq.poll();
    set.remove(min);
    return min;
}

public void addBack(int num) {
    if(set.add(num)) pq.offer(num);
}

2542. 最大子序列的分数

先是想着dfs暴力枚举所有的组合，果然就超时了

看题解，才发现，有序，真是一个很好的性质

先将nums1和nums2同步排序，排序规则按照nums2降序
然后枚举num2[i[为min的情况，只能往<i的下标处寻找了，也就是需要之前当前前k个最大的数，一个小根堆(循环过程中动态维护)就够啦
.
nums2[i] 作为min 那么只能到下标[0,i]去找元素了
最大的k个，小根堆喽 // 每次都是接着前面加入元素所以小根堆写在外面就可以一直维护前i个元素的最大k个值了

public long maxScore(int[] nums1, int[] nums2, int k) {
    int n = nums1.length;
    List<int[]> list = new ArrayList<>();
    for (int i = 0; i < n; i++) list.add(new int[]{nums1[i], nums2[i]});

    Collections.sort(list, ((o1, o2) -> o2[1] - o1[1]));

    PriorityQueue<Integer> pq = new PriorityQueue<>();
    long sum = 0, max = 0;
    for (int i = 0; i < list.size(); i++) {
        int n1 = list.get(i)[0], n2 = list.get(i)[1];
        if (i <= k - 1) {
            pq.offer(n1);
            sum += n1;
        } else {
            if (n1 > pq.peek()) {
                sum -= pq.poll();
                pq.offer(n1);
                sum += n1;
            }
        }
        if (i >= k - 1) max = Math.max(max, sum * n2);
        // nums2[i] 作为min  那么只能到下标[0,i]去找元素了
        // 最大的k个，小根堆喽   // 每次都是接着前面加入元素  所以小根堆写在外面  就可以一直维护前i个元素的最大k个值了
    }
    return max;
}

同样的思路，不一样的写法，感觉更简单一点

public long maxScore(int[] nums1, int[] nums2, int k) {
    int n = nums1.length;
    Integer[] idx = new Integer[n];
    for (int i = 0; i < n; i++) idx[i] = i;
    Arrays.sort(idx, (i, j) -> nums2[j] - nums2[i]);//这里idx 必须包装类型 基本类型报错
    // 只对下标排序就行了  编码功底呀
    //for (int i = 0; i < n; i++)  prints(nums1[idx[i]],nums2[idx[i]]);
    PriorityQueue<Integer> minHeap = new PriorityQueue<>();
    long sum = 0, max = 0;
    for (int j = 0; j < idx.length; j++) {
        int i = idx[j];
        if (j <= k - 1) {
            minHeap.offer(nums1[i]);
            sum += nums1[i];
        } else {
            if (nums1[i] > minHeap.peek()) {
                sum -= minHeap.poll();
                minHeap.offer(nums1[i]);
                sum += nums1[i];
            }
        }
        if (j >= k - 1) max = Math.max(max, sum * nums2[i]);
    }
    return max;
}

374. 猜数字大小

374. 猜数字大小
水题，但是需要点阅读理解

注意java random.nextInt(区间长度) 1~Integer.MAX_VALUE 由于左闭右开 [1,1+Integer.MAX_VALUE) 右边会越界，因此得用nextLong
或者换用别的更好的API

public class lc374 {

    static int pick;

    private int guess(int num) {
        if (pick < num) return -1;
        else if (pick > num) return 1;
        else return 0;
    }

    public int guessNumber(int n) {
        Random rd = new Random();
        long l = 0, r = n;
        while (true) {
            long num = rd.nextLong(r-l+1) + l;//[l,r]的随机数  传入的参数是区间长度
            int g = guess((int) num);
            if (g == -1) r = num;
            else if (g == 1) l = num;
            else return (int) num;
        }
    }

    public static void main(String[] args) {
        test(10, 6);
        test(100, 50);
        test(2147483647, 2147483647);
    }

    private static void test(int n, int pick) {
        //System.out.print(n+" ");
        //System.out.println(pick);
        lc374 t = new lc374();
        lc374.pick = pick;
        int ans = t.guessNumber(n);
        System.out.println(ans);
    }
}

2300. 咒语和药水的成功对数

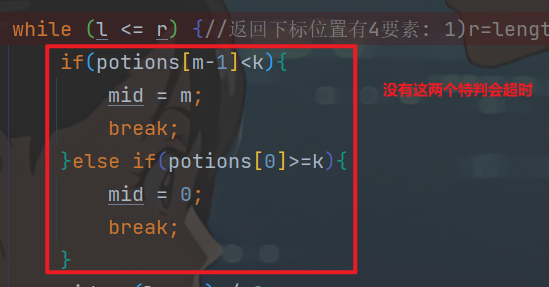
有两个特殊用例，特判的。

在这里插入图片描述

// 有序是一个很好的性质
public int[] successfulPairs(int[] spells, int[] potions, long success) {
    int[] ans = new int[spells.length];
    int n = spells.length, m = potions.length;
    Arrays.sort(potions);
    for (int i = 0; i < n; i++) {
        // 这里可以二分查找k (满足要求的最小的potions[j]) //排序+自己的算法 就都是 n*logn了
        int k = (int) Math.ceil(success*1.0 / spells[i]);
        int l = 0, r = m-1;
        int mid = 0;

        while (l <= r) {//返回下标位置有4要素: 1)r=length-1 2)l<=r  3)r=mid-1 l=mid+1 4) 找不到l是插入位置
            if(potions[m-1]<k){
                mid = m;
                break;
            }else if(potions[0]>=k){
                mid = 0;
                break;
            }
            mid = (l + r) / 2;
            if (potions[mid] < k) l = mid+1; //
            else if (potions[mid] > k) r = mid-1;
            else break;
        }
        if (l > r) mid = l;
        while (mid>0&&potions[mid-1]==k) mid--;//有重复的元素 这个算法选的是靠右边的一个
        ans[i] = m - mid;
        //print(ans);
    }
    return ans;
}

162. 寻找峰值

先暴力O(n)

public int findPeakElement(int[] nums) {
    if(nums.length==1) return 0;
    for (int i = 0; i < nums.length; i++) {
        if(i==0){
            if(nums[i]>nums[i+1]) return 0;
        }else if(i==nums.length - 1){
            if(nums[i]>nums[i-1]) return i;
        }else {
            if(nums[i]>nums[i-1]&&nums[i]>nums[i+1]) return i;
        }
    }
    return -1;
}

O(n)的话最简单的做法就是找最大值了

public int findPeakElement(int[] nums) {
    int maxi = 0;
    for (int i = 0; i < nums.length; i++) {
        if(nums[i]>nums[maxi]) maxi=i;
    }
    return maxi;
}

题解最优做法

“只要数组中存在一个元素比相邻元素大，那么沿着它一定可以找到一个峰值” 的解释：最坏的情况是该方向一直在增大，没有减小，那么找到边界值时因为有-∞的存在，保证了至少边界值会是答案。若中间有下降，那么下降处就是答案。

代码如下

中间隔了好几天才来写的，可能不是很好

public int findPeakElement(int[] nums) {
    if(nums.length==1) return 0;
    int m = nums.length/2;
    if(nums[m]>nums[m-1]){
        for(int i=m+1;i<nums.length;i++) {
            if(nums[i]<nums[i-1]) return i-1;
        }
        return nums.length-1;
    }else {
        for(int i=m-1;i>0;i--) {
            if(nums[i-1]<nums[i]) return i;
        }
        return 0;
    }
}

875. 爱吃香蕉的珂珂

自认为比较暴力且容易超时的写法，但是通过了

private int countTime(int[] piles, int k) {
    int ans = 0;
    for (int i = 0; i < piles.length; i++) {
        ans += Math.ceil(piles[i] * 1.0 / k);
    }
    return ans;
}

public int minEatingSpeed(int[] piles, int h) {
    int max = Arrays.stream(piles).max().getAsInt();
    int l = 1, r = max;
    while (l <= r) {
        int mid = (l + r) / 2;
        int ans = countTime(piles, mid);
        if (ans > h) l = mid + 1;
        else r = mid - 1;
    }
    return l;
}

语法层面优化代码，时间快了接近10倍（50ms->6ms）

private int countTime(int[] piles, int k) {
    int ans = 0;
    for (int p: piles) {//增强for比fori快
        ans += (p+k-1)/k;//改成定点数运算 累积起来比浮点数要快多了
    }
    return ans;
}

public int minEatingSpeed(int[] piles, int h) {
    //int max = Arrays.stream(piles).max().getAsInt();
    int l = 1, r = 0;
    for (int pile : piles) {
        r = Math.max(r,pile);//比Stream流要快
    }

    while (l <= r) {
        int mid = (l + r) / 2;
        long ans = countTime(piles, mid);//这里写int结果不会溢出 强转后也不会溢出
        if (ans > h) l = mid + 1;
        else r = mid - 1;
    }
    return l;
}

216. 组合总和 III

第一感dfs搜索，枚举组合

public List<List<Integer>> combinationSum3(int k, int n) {
    List<List<Integer>> ans = dfs(k, n, 1, new ArrayList<>(), new ArrayList<>());
    return ans;
}


private List<List<Integer>> dfs(int k, int n,int i,List<Integer> curr,List<List<Integer>> ans){
    if(k==0){
        if(n==0) ans.add(new ArrayList<>(curr));
        return ans;
    }
    if(i>9) return ans;
    dfs(k,n,i+1,curr,ans);//不选i
    curr.add(i);
    dfs(k-1,n-i,i+1,curr,ans);//选i
    // 千万退栈时删除 每次都删最后一个 就能保证每次删的就是i
    curr.remove(curr.size()-1);
    return ans;
}

果然就是这么简单

790. 多米诺和托米诺平铺

应该是和斐波那契那样比较简单的dp

dp[i]= max{dp[i-1]+1,dp[i-2]+2,dp[i-3]+5}

1318. 或运算的最小翻转次数

public int minFlips(int a, int b, int c) {
    int count=0;
    int c1,c2,c3;
    while (a!=0||b!=0||c!=0){
        c1 = a&1; c2 = b&1; c3 = c&1;
        //System.out.println(c1+" "+c2+" "+c3);
        if((c1|c2)!=c3){
            if(c3==0){
                count += (c1+c2);
            }else {//c3==1
                count += 1;//把1个0变成1就行了
            }
        }
        a>>=1;b>>=1;c>>=1;
    }
    return count;
}

很简单一题，竟然做了半小时，唉。现在要练的是速度了！！！！

1268. 搜索推荐系统

先暴力，暴力拿分也是一种能力。

别说拿分了，竟然直接就通过了

public List<List<String>> suggestedProducts(String[] products, String searchWord) {
    List<List<String>> ans = new ArrayList<List<String>>();
    Arrays.sort(products);//字典序排序
    //print(products);
    for (int i = 0; i < searchWord.length(); i++) {
        String prefix = searchWord.substring(0, i + 1);
        //System.out.println(sub);
        ArrayList<String> list = new ArrayList<>();
        for (String product : products) {
            if(product.startsWith(prefix)){
                list.add(product);
            }
            if(list.size()==3) break;
        }
        ans.add(list);
    }
    return ans;
}

用字典树反而慢了，奇怪，自己写法不对哦

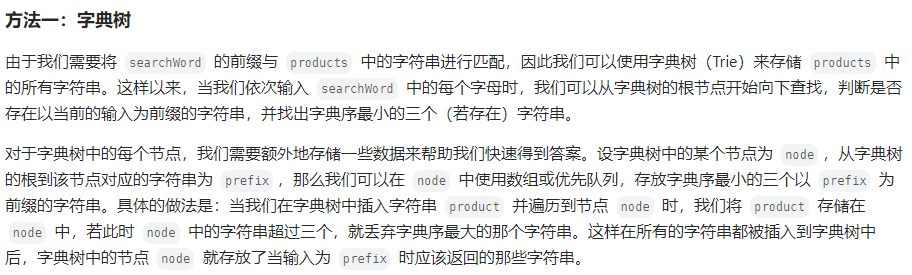
看题解：
字典树得使用很灵活，关键在于字典树结构的设计，本题也是，关键点在于每个node上维护3个字典序最小的3个字符串
这样才能达到O(1)

插入时同时每个节点维护一个字符串队列

在这里插入图片描述

// 得修改字典树结构
class Trie {
    Trie[] next = new Trie[26];
    // 维护最小的3个要用大根堆 (默认是小根堆)
    PriorityQueue<String> pq = new PriorityQueue<>((o1,o2)->o2.compareTo(o1));
    public Trie() {}
    public void insert(String word) {
        Trie node = this;
        for (int i = 0; i < word.length(); i++) {
            int n = word.charAt(i) - 'a';
            if (node.next[n] == null) {
                node.next[n] = new Trie();
            }
            node = node.next[n];
            // 插入的时候后插 // 下面查的时候也后查就行了
            if(node.pq.size()<3)  node.pq.offer(word);//一定写node.pq而不是pq 否则都加到头节点上去了
            else if((node.pq.peek().compareTo(word)>0)){
                node.pq.poll();
                node.pq.offer(word);
            }
        }
    }
}

public class LC1268_字典树 extends Solution {

    public List<List<String>> suggestedProducts(String[] products, String searchWord) {
        List<List<String>> ans = new ArrayList<List<String>>();
        Trie t = new Trie();
        for (String product : products) {
            t.insert(product);
        }

        Trie node = t;
        for (int i = 0; i < searchWord.length(); i++) {
            LinkedList<String> list = new LinkedList<String>();
            int n = searchWord.charAt(i) - 'a';
            if (node.next[n] == null) {
                ans.add(list);
                node = new Trie();//到一个空结点上去走完接下来所有的null
                continue;
            }
            node = node.next[n];
            // 走一趟就可以搜集所有了 多快啊 这就是前缀树
            while (!node.pq.isEmpty()){//也要加上node
                list.addFirst(node.pq.poll());
            }
            ans.add(list);
        }
        return ans;
    }
｝

在这里插入图片描述
调了好久才调到15ms，感觉是现在的极限了。

时间花费太多，这一题，彻底失败！唉

435. 无重叠区间

先用分治思想，莫名其妙通过了

public int eraseOverlapIntervals(int[][] intervals) {
    Arrays.sort(intervals, new Comparator<int[]>() {
        @Override
        public int compare(int[] o1, int[] o2) {
            if (o1[1] != o2[1]) return o1[1] - o2[1];
            return o1[0] - o2[0];
        }
    });
    //print2(intervals);
    int ans = 0;
    int p = Integer.MIN_VALUE;
    for (int i = 0; i < intervals.length; i++) {
        if(intervals[i][0]>=p){
            p = intervals[i][1];
            ans++;
        }
    }

    return intervals.length-ans;
}

但是很慢：
在这里插入图片描述
排序太耗时了

看了看题解，发现，时间复杂度一样，思路也一样，为何我的慢？原来这里不求区间长度，只求区间个数，所以有一级排序就够了

public int eraseOverlapIntervals(int[][] intervals) {
    Arrays.sort(intervals, (a,b)->a[1]-b[1]);
    int ans = 0;
    int p = Integer.MIN_VALUE;
    for (int i = 0; i < intervals.length; i++) {
        if(intervals[i][0]>=p){
            p = intervals[i][1];
            ans++;
        }
    }
    return intervals.length-ans;
}

在这里插入图片描述
也就优化了那么一点点，差别不大

算法笔记 4.4 贪心区间贪心

452. 用最少数量的箭引爆气球

这两题就是初学贪心时的两个例题，都不难算法笔记 4.4 贪心区间贪心

这一题在上一题基础上，points[i][0]>=p 改成points[i][0]>p，然后直接返回ans就行了
然后测试数据边界值很恶心，得用Long和CompareTo方法比较大小，直接减法越界错误

public int findMinArrowShots(int[][] points) {
    Arrays.sort(points, new Comparator<int[]>() {
        @Override
        public int compare(int[] o1, int[] o2) {
            Integer a = o1[1];
            Integer b = o2[1];
            return a.compareTo(b);//不能用减号 测试用例有极端值 (相减越界)
        }
    });

    //print2(points);
    Long p = Long.MIN_VALUE;//边界值太恶心了 得用Long
    int ans = 0;
    for (int i = 0; i < points.length; i++) {
        if(points[i][0]>p) {//等号去掉 相等也算一个区间
            p = (long) points[i][1];
            ans++;
        }
    }
    return ans;
}

思路没问题，时间复杂度也没问题，差别在于语法上，稍微简化一下，不必死扣

public int findMinArrowShots(int[][] points) {
    Arrays.sort(points, new Comparator<int[]>() {
        @Override
        public int compare(int[] o1, int[] o2) {
            return (o1[1] < o2[1]) ? -1 : ((o1[1] == o2[1]) ? 0 : 1);
            //不能用减号 测试用例有极端值 (相减越界)
        }
    });

    //print2(points);
    Long p = Long.MIN_VALUE;//边界值太恶心了 得用Long
    int ans = 0;
    for (int i = 0; i < points.length; i++) {
        if(points[i][0]>p) {//等号去掉 相等也算一个区间
            p = (long) points[i][1];
            ans++;
        }
    }
    return ans;
}

public int findMinArrowShots(int[][] points) {
    Arrays.sort(points, (o1,o2)-> {return (o1[1] < o2[1]) ? -1 : ((o1[1] == o2[1]) ? 0 : 1);});
    Long p = Long.MIN_VALUE;//边界值太恶心了 得用Long
    int ans = 0;
    for (int i = 0; i < points.length; i++) {
        if(points[i][0]>p) {//等号去掉 相等也算一个区间
            p = (long) points[i][1];
            ans++;
        }
    }
    return ans;
}

901. 股票价格跨度

5min没想出来，就先暴力拿分，这也是一种能力

太离谱了，暴力都暴力了20min。怎么能行，还得练哦，至少500题

class StockSpanner {
    ArrayList<Integer> prices = new ArrayList<>();
    public StockSpanner() { }
    public int next(int price) {
        prices.add(price);
        int j = prices.size()-2;
        int ans = 1;
        while (j>=0&&prices.get(j)<=price) {
            j--;
            ans++;
        }
        return ans;
    }
}

这也是单调栈，咋就看不出来呢
即需要求出每个值与上一个更大元素之间的下标之差

光脑子想是想不出来的，动手在草稿纸上画图，一画就出来了，

每次next时可以直接将栈内小的弹出，因为记录的是下标，所以弹出比我小的，然后把我压栈是可行的，因为要是比我大，前面更小的肯定也要弹栈，要是比我小，连续性导致到我即断裂

所谓维护一个单调不减的单调栈即可，这才是单调栈的核心

!!!单调栈

class StockSpanner {
    Deque<int[]> st = new LinkedList<int[]>();
    int k = 0;
    public StockSpanner() {
        st.push(new int[]{-1, Integer.MAX_VALUE});
    }
    public int next(int price) {
        while (st.peek()[1] <= price) st.poll();
        int ret = k - st.peek()[0];
        st.push(new int[]{k++, price});
        return ret;
    }
}