数据信息的表示

• 数值数据
• 非数值数据

数值数据的表示

计算机采用二进制原因

• 易于物理实现
• 运算规则简单
• 机器可靠性高
• 逻辑判断方便

进位计数制

指计算机采用从低位向高位进位的方式计数

补码

其实就是利用同余系把数映射到[0,2^n)范围进行运算

移码

常用于表示浮点数的阶码，当偏移量取$2^{n-1}$，其真值对应的移码定义是为$[X{]}_{移}=2^{n-1}+X$。即把补码的符号位取反。

定点数与浮点数

• 定点数：小数点位置固定，数据范围有限，硬件简单。
• 浮点数：小数点位置浮动，数据范围很大，硬件复杂。

IEEE标准中，三元组{S,E,M}来表示一个数，尾数M的最高有效位总为1，所表示实际值为1.M。

阶码表示指数的操作：避免出现正负指数，还可以保持数据的原有大小数据，便于进行比较。

例：

非数值数据的表示

字符与字符串的表示

• ASCII字符
• Unicode码
• 字符串

汉字的编码方法

• 输入码
• 交换码
• 机内码
• 字形输出码与汉字库

数据信息的校验

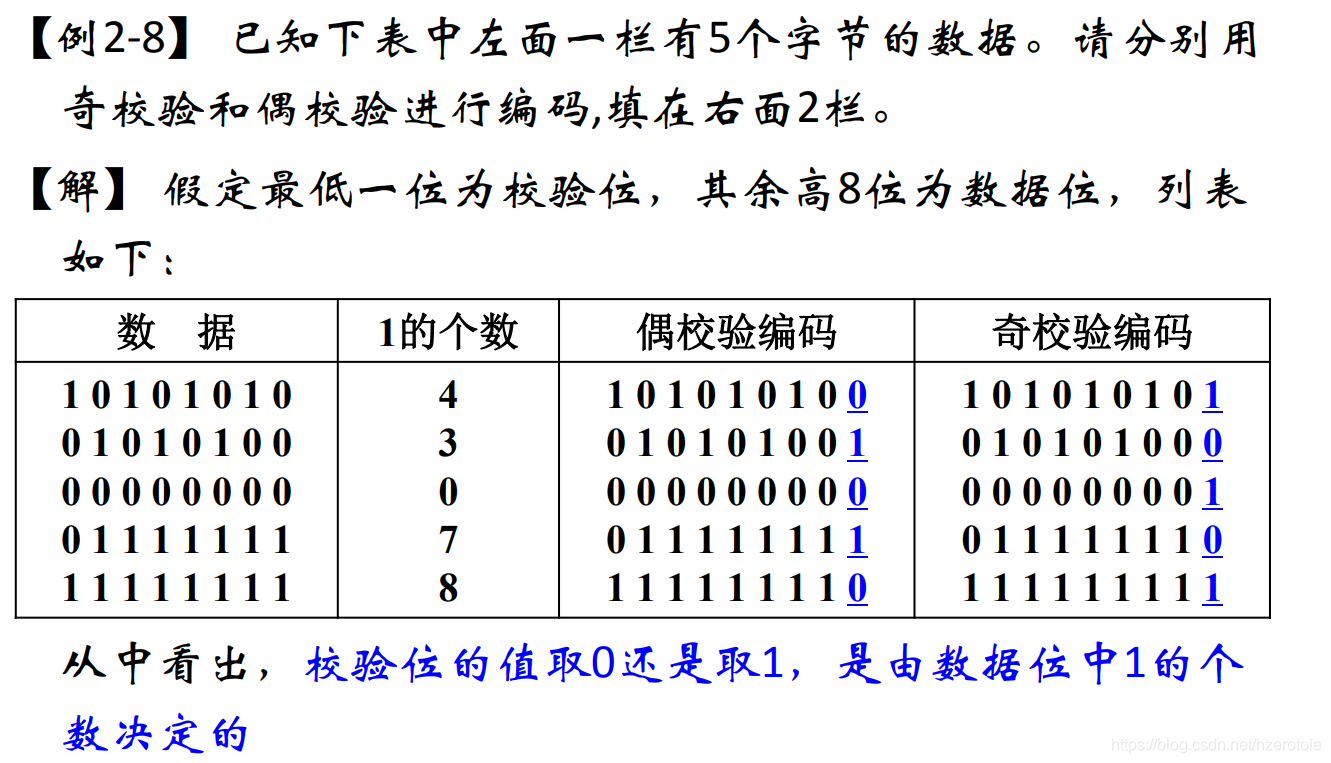
奇偶校验

• 可以检测出一位或奇数位错误，但不能确定出错的位置，也不能检测出偶数位错误。（一位出错的概率比多位出错的概率高得多）

简单奇偶校验

• 方式为在原信息中加上一位校验位组成校验码，这个校验位的作用是使得原有效信息中，“1”的个数为奇数个。
• 以奇校验为例，形成方式为原信息串求异或和后取反。
• 校验检测时，信息位和校验位异或和为0则代码无错误。但出现错误时，无法确定位置。

例题

交叉奇偶校验

• 纵向、横向同时校验

• 大量的数据块传送时，不仅在每个字节内部横向校验，并且全部字节同一位也设置奇偶检验做纵向校验。

定点运算和定点运算器

基本运算

• 算术运算
• 逻辑运算

定点加、减法运算

补码加法公式——$[x{]}_{补}+[y{]}_{补}$