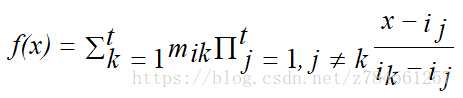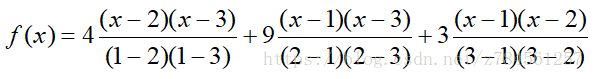文章仅仅用来构建知识框架工后续的复习使用，本文章是转载于其他博文，原文链接：https://blog.csdn.net/z784561257/article/details/82942581

假设一个秘密s，秘密分发者将s运用某种特定的算法分成n份，然后将n份分别分发给n个参与者。

在重构时，在n个参与者中选取t个人来重构这个秘密s。任意的t个人都可以重构，任意的t-1个参与者无法获得秘密的任何信息。

举个例子说明一下：

假设有多项式：

在这个所有的值都必须模取一个素数，这里取的是13.

假设秘密s被隐藏在多项式中，也就是常数项1，我们分别将x=1,2,3,4代入求得：

这里的n=4,这4个人分别拿到的秘密为4，9，3，12

当然这是一个二次多项式，所以t=3，我们任意的取三组数据就可以恢复上面的多项式，任意的(t-1=)2组数据无法恢复多项式。

我们可以列一个方程组即可求得一元二次方程。

或者我们可以用插值多项式进行恢复，其实道理都是一样的。

插值多项式的公式：

我们可以将前三组代入上面的公式中可以得到:

当化解完后，就是上面的多项式，这样就可以得到秘密s了。

当然这里的x的值，可以任意的取值，我在这里就是举了一个例子。

本文禁止抄袭，转载请注明地址。

下面是找的一本书上的图片内容，可以对照阅读：