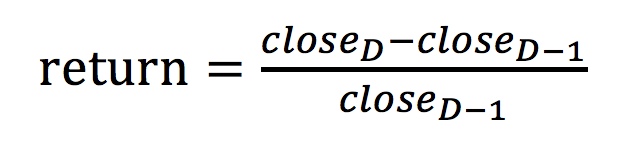一、多因子筛选阶段介绍
1、 筛选阶段的任务
基本面数据因子(特征)如此之多,那么如何去找到对应的对股票收益率比较好的。并且能在未来一段时间给我们的选股收益率提供帮助。
2、挖掘因子的过程
我们可以大概从这几个方面去做
- 1、先从上百个因子当中分析出对股票收益率有效的部分因子(这个数量可以根据筛选的严格程度去做)
- 在每个大类因子当中去做筛选,每个大类因子中筛选出有效的N个因子
- 质量、估值、成长等因子
- 严格:例如20个有效因子
- 不严格:例如50个有效因子
- 在每个大类因子当中去做筛选,每个大类因子中筛选出有效的N个因子
- 2、在筛选的单个因子当中做相关性分析,合并相关性强的因子
- 最终得出有效的,相关性弱的因子,数量不多,一般在10个左右
海选—>N个因子—>精选—>n个因子
N > n
二、单因子有效性分析目的
1、 有效性分析确定的几个问题
- 因子的IC分析
- 确定因子的正负性
- 对收益率提供正面还是负面的影响
- 因子的收益率分析
- 确定因子的方向
什么是因子的方向?
| 因子方向 | 因子说明 |
|---|---|
| 因子升序 | 因子值越小越好,如市值、估值类(市盈率、市净率、市销率等) |
| 因子降序 | 因子值越大越好,如ROE、利润、利润增长率类因子 |
| 因子中性 | 因子方向不确定,如周转率、资产负债率等因子 |
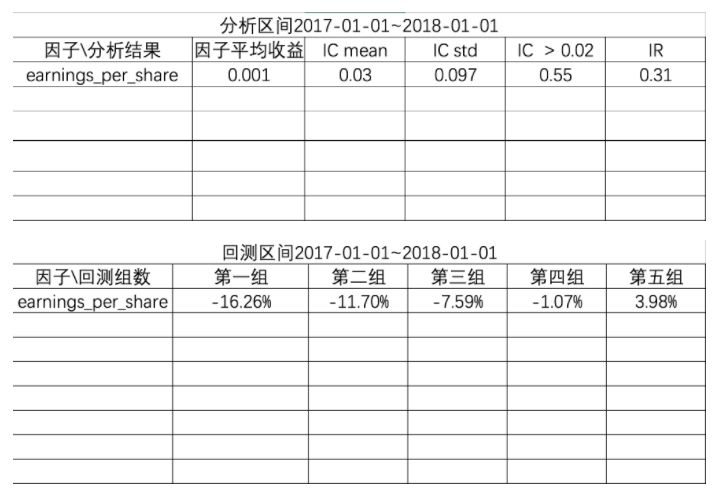
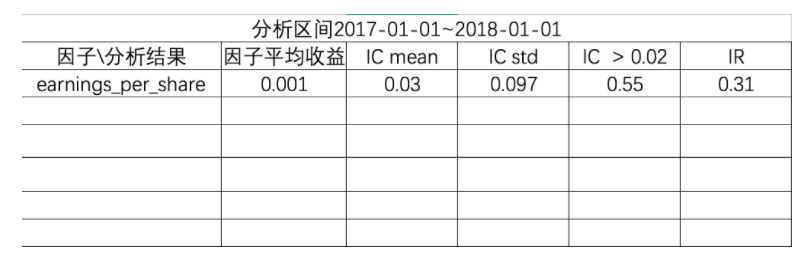
利用这两个分析方式去筛选,最终我们要得出这样的两张表。
三、单因子有效性分析-因子IC分析
因子的IC分析需要确定的是因子与收益率之间的相关性,提供给筛选的依据。也就是这张表格中的IC相关值
- IC mean:因子IC的平均值
- IC std:因子IC的标准差
- IC > 0.02:因子IC大于0.02的比例
- 这里大于0.02可修改,如果更大,那么意味着筛选更加严格
- IR : 信息比率
在这里我们以分析估值类当中的部分因子。
1、 信息系数定义
某一期的IC指的是该期因子暴露值和股票下期的实际回报值在横截面上的相关系数
1.1 什么是因子暴露度
指的就是因子本身的值
1.2 计算方式
- 斯皮尔曼相关系数(Rank IC)
- 斯皮尔曼相关系数表明 X (独立变量) 和 Y (依赖变量)的相关方向。 如果当X增加时, Y 趋向于增加, 斯皮尔曼相关系数则为正
- 与之前的皮尔逊相关系数大小性质一样,取值 [-1, 1]之间
即某时点某因子在全部股票因子暴露值排名与其下期回报排名的截面相关系数。
1.3 信息系数API
- import scipy.stats as st
- st.spearmanr(fund['pe_ratio'], fund['return'])
但是现在我们知道因子值怎么获取,但是某段时间的收益怎么来?
2、 如何求收益率
2.1 收益率区间
- 按照区间大小或者研究的区间大小
- 日收益率
- 月收益率
- 年收益率
2.2 计算公式
- 计算公式,例如:当前区间D的收益率
公式解读:这期收盘价减上期收盘价/ 上期收盘价
计算收益率时,假如是月收益率,就认定每月最后一天价格作为当月的价格
3、 案例:单因子某天的IC分析
比如我们需要计算2017-01-03的因子IC值
3.1 分析
- 1、获取这一天因子数据
- 2、获取2017-01-03与2017-01-04的价格数据,计算2017-01-04的收益率(下期收益率)
- 3、计算相关系数
3.2 代码
# 1、获取因子数据
q = query(fundamentals.eod_derivative_indicator.pe_ratio)
fund = get_fundamentals(q, entry_date="2017-01-03")[:, 0, :]
# 2、获取当天和下一期的收盘价格
price_n = get_price(list(fund.index), start_date="2017-01-03", end_date="2017-01-03", fields="close").T
price_next = get_price(list(fund.index), start_date="2017-01-04", end_date="2017-01-04", fields="close").T
# 计算收益率, 填充缺失值
price_now.iloc[:, 0].fillna(price_now.iloc[:, 0].mean(), inplace=True)
price_next.iloc[:, 0].fillna(price_next.iloc[:, 0].mean(), inplace=True)
# 下期价格- 当前价格/ 当前价格, 这里计算的是下期的收益率 2017-01-04
return_price = price_next.iloc[:, 0]/price_now.iloc[:, 0] - 1
# 计算相关系数,是一个值,在[-1, 1] IC
st.spearmanr(fund.iloc[:, 0], return_price)使用更加强大的工具去计算IC值
4、因子分析工具-Alphalens
官网地址: http://quantopian.github.io/alphalens/index.html
4.1 alphalens的数据结构
在做分析之前,需要准备所有分析所需的数据格式,事前需 要准备好因子数据、 价格数据和行业分组数据。 行业数据可有可无,若有则可以设臵成 Dict 格式或者 Series 格式
- alphalens.utils.get_clean_factor_and_forward_returns(factor, prices, groupby=None, quantiles=5, bins=None, periods=(1, 5, 10), filter_zscore=20, groupby_labels=None, by_group=bool, max_loss=0.35)
| 参数 | 类型 | 说明 |
|---|---|---|
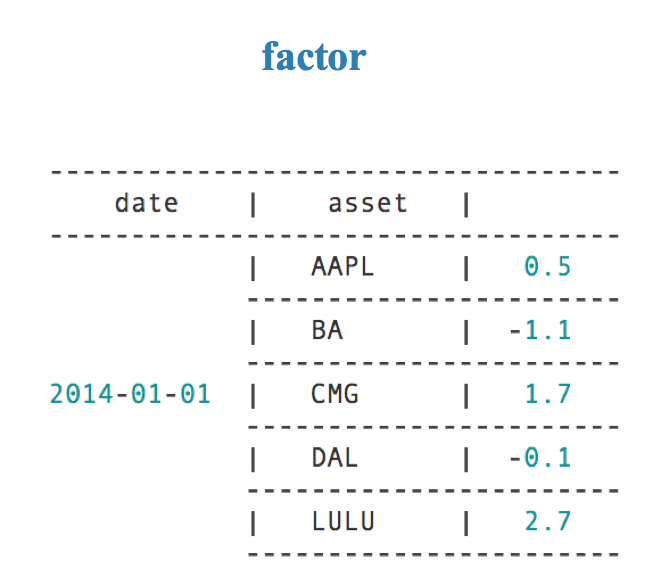
| factor | pd.Series – MultiIndex | 一次一个因子数据,MultiIndex系列由时间戳(级别0)和资产(级别1)索引,包含单个alpha因子的值 |
| price | pd.DataFrame | 所有股票的多天价格数据 |
| groupby | pd.Series - MultiIndex或dict | 行业分组信息, 保证每个股票都有行业分类 |
| periods=(1, 5, 10) | tuple | 默认计算了远期收益(预测能力) |
| groupby_labels | dict | 分组名称, 把所有的 行业贴上标签。比如说,(煤炭)中信对应数字 1,(钢铁)中信对应数字 2,以此类推。 |
| max_loss=0.35 | float | 计算允许因子数据丢弃的最大百分比(0.00到1.00),(例如NaN),未提供足够的价格数据来计算所有因子值的远期收益率,设置max_loss = 0避免数据出现缺失 |
| by_group | bool | 分组计算可以理解成是传统的行业中性的做法 |
| return: merged_data: | pd.DataFrame - MultiIndex | 收益率、行业分组信息 |
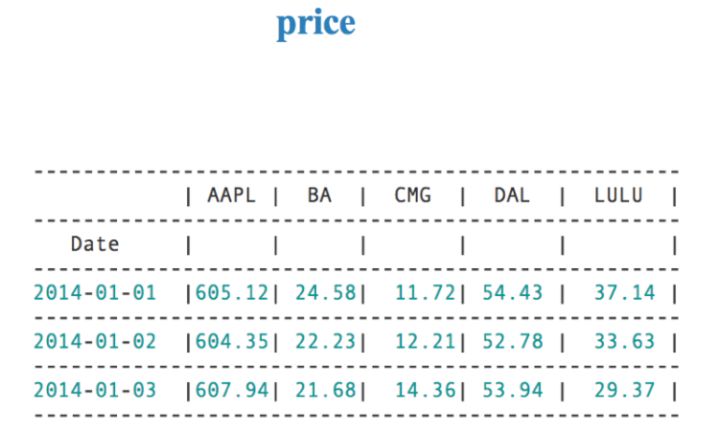
factor格式如下图:
price格式如下图:
4.2 Alphalens API
from alphalens import performance
from alphalens import plotting
from alphalens import tears
from alphalens import utils- 获取综合信息
- alphalens.tears.create_summary_tear_sheet(factor_data, long_short=True, group_neutral=False)
- 一个简易的summary包含几种综合分析
- alphalens.tears.create_summary_tear_sheet(factor_data, long_short=True, group_neutral=False)
- 因子IC 分析
- alphalens.performance.factor_information_coefficient(factor_data, group_adjust=False, by_group=False)
- 计算因子值和预期收益之间的基于Spearman等级相关的信息系数(IC)(默认每天)
- 返回IC dataframe
- factor_data:按日期(级别0)和资产(级别1)索引的MultiIndex DataFrame,包含单个alpha因子的值,每个期间的正向收益
- group_adjust: 是否行业分组
- by_group: 分组计算
- return: ic DataFrame
- alphalens.tearse.factor_alpha_beta(factor_data, returns=None, demeaned=True, group_adjust=False, equal_weight=False)
- 计算alpha和beta
- alphalens.tears.create_information_tear_sheet
- alphalens.performance.factor_information_coefficient(factor_data, group_adjust=False, by_group=False)
- 因子收益率系数分析
- alphalens.tears.create_returns_tear_sheet(factor_data, long_short=True,group_neutral=False, by_group=False)
5、 案例:使用alphalens进行单个因子的IC 分析
5.1 结果
我们确定要分析的区间,一般来讲分析因子以最近的2~3年时间,看效果较好的因子。这里我们分析质量因子当中的earnings_per_share因子
5.2 分析
- 准备因子series结构
- 去极值
- 标准化
- 准备价格数据
- 使用alphalens进行因子IC计算分析
5.3 代码
1、准备因子series结构
# 获取时间 pd.date_range获取是周一~周五, 没有除去假期
# 需要使用get_trading_dates
date = get_trading_dates(start_date="2017-01-01", end_date="2018-01-01")
# 定义一个装有所有天所有股票的因子数据
all_data = pd.DataFrame()
# 根据时间获取因子数据 每股收益earnings_per_share
for i in range(len(date)):
q = query(fundamentals.financial_indicator.earnings_per_share)
fund = get_fundamentals(q, entry_date=date[i])[:, 0, :]
# 构造date时间列
fund['date'] = date[i]
# 将所有每次循环的fund,都拼接到all_data当中
all_data = pd.concat([all_data, fund])
# 设置multiindex 的dataframe
all_data = all_data.set_index(['date', all_data.index])
# 因子的数据处理,去极值,标准化
all_data['earnings_per_share'] = mad(all_data['earnings_per_share'])
all_data['earnings_per_share'] = stand(all_data['earnings_per_share'])
# all_data multiIndex DataFrame --->multiIndex series
single_factor_series = all_data['earnings_per_share']2、准备价格数据
# 获取所有股票代码列表
stocks = all_instruments('CS')
stocks_list = stocks['order_book_id']
# 获取指定时间的价格数据
price = get_price(list(stocks_list), start_date="2017-01-01", end_date="2018-01-01", fields='close')3、因子IC计算
from alphalens import performance
from alphalens import plotting
from alphalens import tears
from alphalens import utils
# 准备一个使用所有alphalens的接口的通用数据
# 使用utils.get_clean_factor_and_forward_returns生成通用数据
factor_return = utils.get_clean_factor_and_forward_returns(single_factor_series, price)
IC = performance.factor_information_coefficient(factor_return)6、 因子IC效果图分析
6.1 三种图形分析
- alphalens.plotting.plot_ic_ts(IC)
- 时间序列图和移动平均线图
- alphalens.plotting.plot_ic_hist(IC)
- 因子分布直方图
- alphalens.plotting.plot_ic_qq(IC)
- 因子Q-Q图
- plotting.plot_monthly_ic_heatmap(IC_month)
- 因子按月热力图
- 结合:计算月的因子IC, 这个月因子数据。和每月最后一个交易日计算出来的价格收益率
- IC_month = performance.mean_information_coefficient(factor_return, group_adjust=False, by_group=False, by_time='1m')
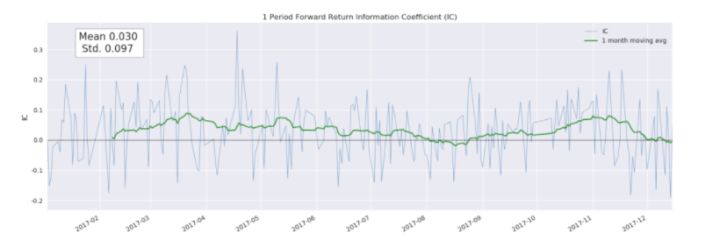
6.2 时间序列与移动平均线图
# 画出因子的时间序列图和移动平均线图
plotting.plot_ic_ts(IC)从时间序列图当中我们可以看出一个因子在时间上的正负性,能清楚知道哪段区间内是正相关、负相关的结果
从中也能得出IC平均值,标准差的大小,就可以填入我们的表格当中
6.3 因子分布直方图
6.4 其它图形查看分析
7、因子有效性分析表格填充
在筛选因子的时候,会考虑某段时间的平均值大小。判断平均值大于某个数字,IC的值一般根据筛选严格程度取值,这个值可以自定义0.06意味筛选严格,> 0.02会放松筛选(可以用在对开始很多因子的海选中)
- IC > 0.02
# 得出IC > 0.02的比例
a = IC.iloc[:, 0]
len(a[a > 0.02])/len(a)8、研报分析
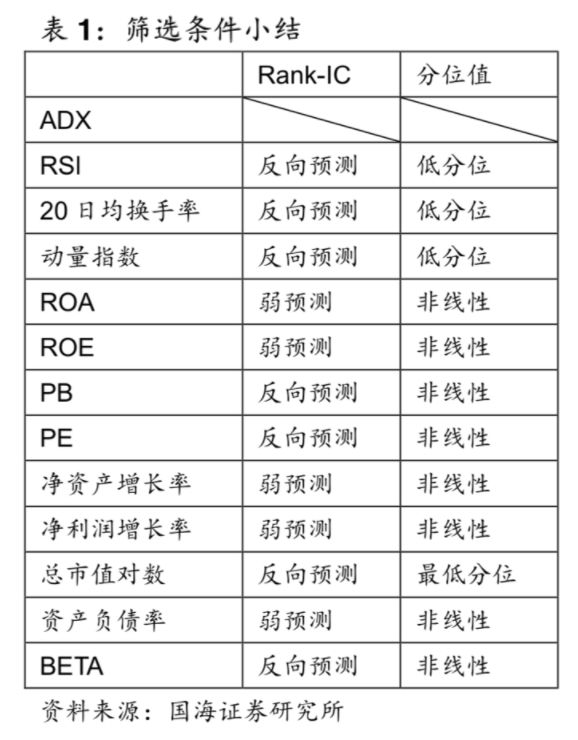
代表:国海证券Rank-IC分析结果剖析
四、单因子有效性分析-因子收益率分析
1、 什么是因子收益率
因子收益率是在固定周期内对因子暴露值和下期的收益率之间建立横截面回归方程。得到的权重系数即为因子收益率
注:默认每天进行横截面回归得到的权重系数值
2、案例:因子收益率计算
2.1 代码
使用create_returns_tear_sheet函数进行计算
# 收益率分析
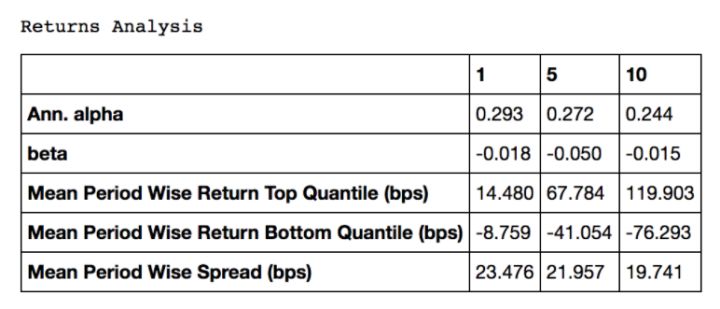
tears.create_returns_tear_sheet(factor_return)2.2 结果分析
2.2.1 计算数值结果
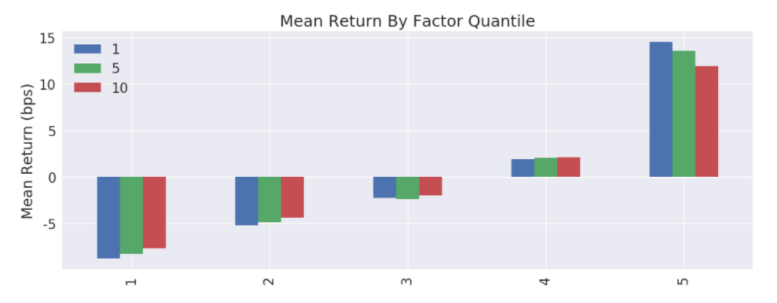
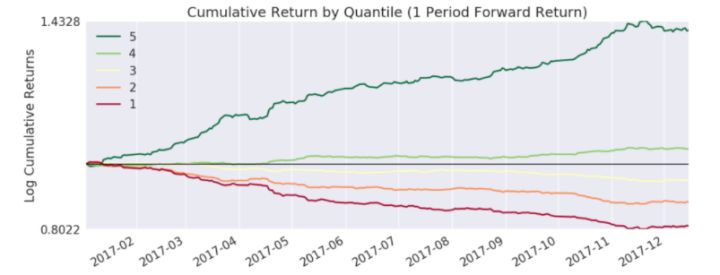
2.2.2 分位数分组结果
从这张图中,我们就能够得出因子在高分位数的股票上表现较好,说明因子的方向为降序,因子越大越好。
当然也可以通过因子累计收益率的分位数分组情况图查看
2.3 因子在周期内的平均收益率
我们的因子有效性分析excel表格当中,需要周期内的计算因子的平均收益率,可以通过以下计算
# 因子的每一期的收益(因子收益)
performance.factor_returns(factor_return).iloc[:, 0].mean()五、单因子测试框架和单因子回测框架搭建
1、单因子测试框架
刚才我们在研究平台上所做的因子IC分析和因子收益率分析都属于因子的测试框架,因为我们使用的第三方平台,所以没有办法做一个比较完整的通用的测试系统。但是目的是为了测试选出表现较好的,如果我们建立好了测试结果?因子分析完了接着做什么?
1.1 将所有统计的因子打分排名
统计完结果之后我们需要对上百个因子进行一次筛选,在这里采取打分排名
- 构建打分依据
- 因子平均收益 >0.002
- IC > 0.02
- IR > 0.3
- 对于3项标准中的每一项进行打分,每满足一项打分为1,然后每个因子看的多少分
注:打分大小看整体情况,以及选出多少因子排名之后可以选出10多个较好的因子,然后做后续相关性分析和合成
2、单因子回测框架
当筛选出部分因子之后,其实我们还要去观察它在回测过程当中真是的收益率情况。所以要建立每个因子的回测框架,主要对不同分位数上的股票收益进行统计。也就是下面这张图
2.1 代码
# 可以自己import我们平台支持的第三方python模块,比如pandas、numpy等。
# 建立单因子的回测框架
# 回测区间 2017-01-01~2018-01-01
# 调仓频率:一个月,买卖判断
import numpy as np
# 在这个方法中编写任何的初始化逻辑。context对象将会在你的算法策略的任何方法之间做传递。
def init(context):
# 在context中保存全局变量
context.quantile = 5
scheduler.run_monthly(factor_rollback, tradingday=1)
def factor_rollback(context, bar_dict):
# 选出因子数据,选出不同组的位置进行回测
q = query(fundamentals.financial_indicator.earnings_per_share)
fund = get_fundamentals(q)
# 进行数据处理
# 变成行是股票、列是指标的数据
factor = fund.T
# 去极值、标准化
factor['earnings_per_share'] = mad(factor['earnings_per_share'])
factor['earnings_per_share'] = stand(factor['earnings_per_share'])
# 求分位数是对于一列数据,dataframe求不了
data = factor.iloc[:, 0]
# 按照分位去分成5组,分别进行回测
# quantie(0.2)
# [0.2, 0.4, 0.6, 0.8]
if context.quantile == 1:
data = data[data <= data.quantile(0.2)]
elif context.quantile == 2:
data = data[(data > data.quantile(0.2)) & (data <= data.quantile(0.4))]
elif context.quantile == 3:
data = data[(data > data.quantile(0.4)) & (data <= data.quantile(0.6))]
elif context.quantile == 4:
data = data[(data > data.quantile(0.6)) & (data <= data.quantile(0.8))]
elif context.quantile == 5:
data = data[data > data.quantile(0.8)]
# 建立回测的股票池
context.stock_list = data.index
# 卖
for stock in context.portfolio.positions.keys():
# 判断股票仓位是否>0
if context.portfolio.positions[stock].quantity > 0:
if stock not in context.stock_list:
order_target_percent(stock, 0)
weight = 1.0 / len(context.stock_list)
# 卖
for stock in context.stock_list:
order_target_percent(stock, weight)
# before_trading此函数会在每天策略交易开始前被调用,当天只会被调用一次
def before_trading(context):
pass
# 你选择的证券的数据更新将会触发此段逻辑,例如日或分钟历史数据切片或者是实时数据切片更新
def handle_bar(context, bar_dict):
# 开始编写你的主要的算法逻辑
pass
# after_trading函数会在每天交易结束后被调用,当天只会被调用一次
def after_trading(context):
pass
def mad(factor):
"""3倍中位数去极值
"""
# 求出因子值的中位数
med = np.median(factor)
# 求出因子值与中位数的差值,进行绝对值
mad = np.median(np.abs(factor - med))
# 定义几倍的中位数上下限
high = med + (3 * 1.4826 * mad)
low = med - (3 * 1.4826 * mad)
# 替换上下限以外的值
factor = np.where(factor > high, high, factor)
factor = np.where(factor < low, low, factor)
return factor
def stand(factor):
"""自实现标准化
"""
mean = factor.mean()
std = factor.std()
return (factor - mean) / std六、分组动手练习
分类因子
| 价值因子 | 质量因子 | 成长因子 |
|---|---|---|
| pe_ratio | return_on_invested_capital | in_revenue |
| pcf_ratio | du_return_on_equity | inc_eps |
| pb_ratio | return_on_asset_net_profit | inc_total_asset |
| market_cap | return_on_equity | inc_net_profit |
| ps_ratio | return_on_asset | inc_earnings_per_share |
| earnings_per_share | inc_operating_revenue | |
| net_profit_to_revenue | revenue |
分组去进行练习,统计在表格当中
七、多因子相关性分析
1、 如何计算因子间的相关性
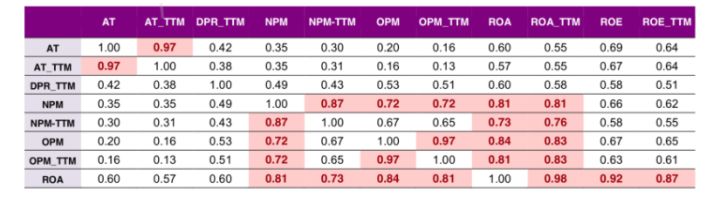
1.1 研报分析结果
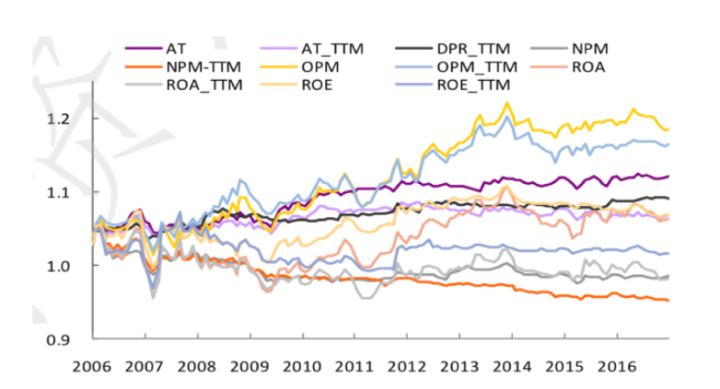
下图是 某大类因子下的一些因子IC值变化图也能够看出大概相关性
比如说OPM和OPM_TTM相关性较强,变化趋势类似
- 某研报最终相关性最终结果
1.2 多因子相关性
相关性分析还是使用斯皮尔曼秩相关系数,但是对象是两个因子的IC值序列分析
1.3 代码
st.spearmanr(IC_return_on_equity.iloc[:, 0], IC_fully__diluted_earnings_per_share.iloc[:, 0])八、多因子合成
1、因子合成
目的:将一些相关(高、低)的因子合成一个因子
- 方法:
- 使用PCA方式(使用于较强相关性)
2、 案例:合成因子
分析
我们之前统计过的earnings_per_share和fully_diluted_earnings_per_share两个因子相关性较高,所以将他们两个进行合成
- 获取因子数据
- 应用PCA进行合成