一、递归的意义
所谓函数递归,就是在某个函数中再次调用这个函数本身,做到函数自己调用自己,这个就是函数的递归。而函数的递归主要是的作用是将一个本身比较复杂,并且步骤繁多的函数逐次的递归使其变得简单化,就比如剥笋:我们想要得到里面能吃的部分,就需要剥笋。而笋的皮有很多层,每剥开一层皮就进入新的一层,直到剥皮这个动作结束。函数递归一次就好比笋剥了一层皮,多次递归,自然就吃到里面的“笋”了。
二、递归的使用条件
通过将大问题变成稍微小一点的问题,然后再把稍微小一点的问题变得更小,直到能够直接解决,再依次从小问题到大问题逐个解决。
光靠说的可能比较难理解,写个最最简单的递归函数帮大家理解一下吧。
#include <stdio.h>
int main()
{
printf("HelloWorld\n");
main();
return 0;
}在这段代码中就是在main函数中调用了它本身,但仔细看来会发现,这段代码只管不断递归main函数,好像并没有出口呀?我们运行代码果然是输出了非常多的HelloWorld。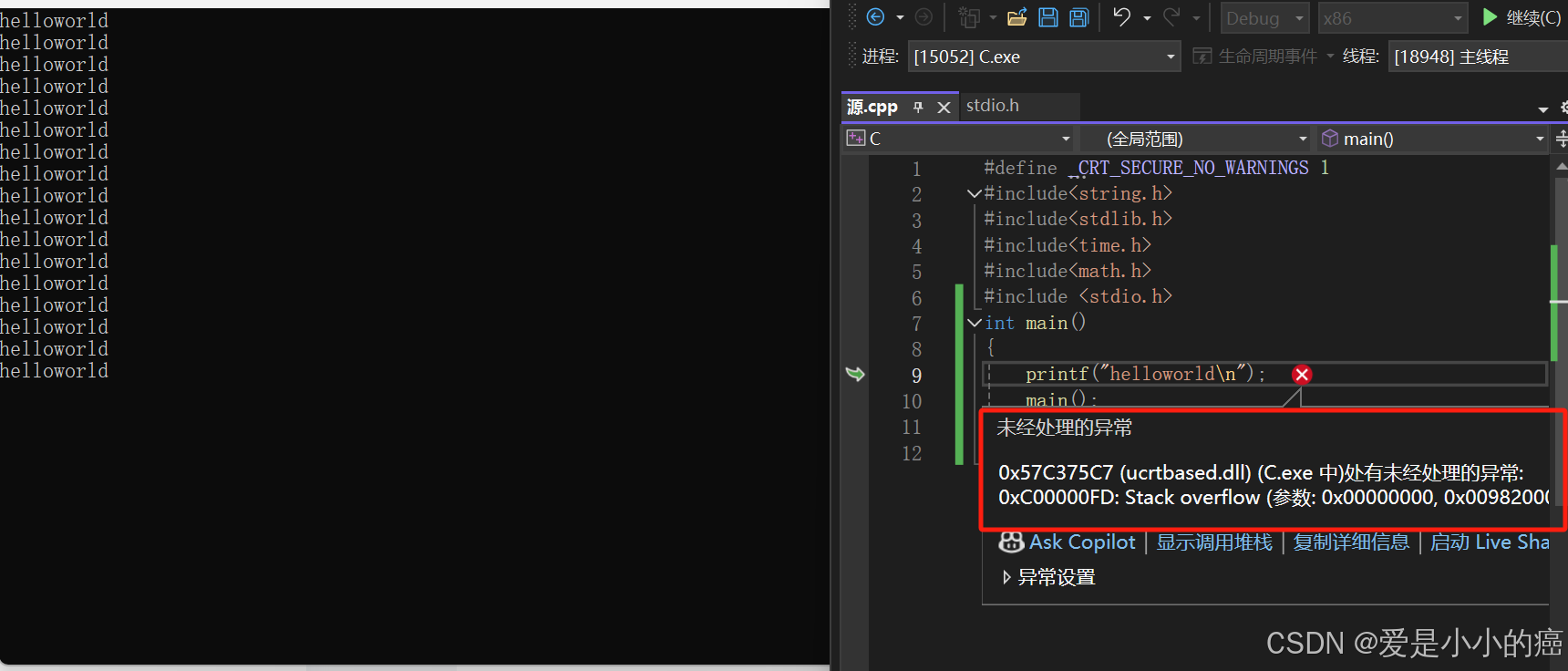
所以我们在使用递归函数的时候,是必须为递归函数创造出一个能够让递归结束的条件的,并且每一次进行函数的递归,都要使函数朝着递归结束的条件更进一步。
我们对这段代码进行一点改造,让它不再陷入死循环造成栈溢出。
#include <stdio.h>
int i;//全局变量未初始化时默认为0
int main()
{
printf("helloworld\n");
i++;//每次调用都会让递归函数向结束条件更近一步
if (i == 10)
return 0;//递归函数的结束条件
main();
return 0;
}运行结果:
三、递归的优点和缺点
1.递归函数的优点
递归函数可以用于很多地方,并且通过递归函数能省去很多步骤,使原本繁琐的问题变得简单易懂,并且代码也要短上许多。就比如让我们来做这道题:输入一个整数,依次打印它的每一位 如果不去用递归函数,用常规的解题方法来思考一下该如何求解:首先我们需要先利用先/10再%10的方法,获取这个整数的每一位数字。
#include <stdio.h>
void Print(int a)
{
int m = 0;
int i = 0;
int j = 0;
int arr[20];
while (a)
{
m = a % 10;
a = a / 10;
arr[i] = m;
i++;
j++;
}
for (i = j-1; i >= 0; i--)
{
printf("%d ",arr[i]);
}
}
int main()
{
int a;
scanf("%d", &a);
Print(a);
return 0;
}常规思想解题有一个问题:我们获取每一位数字后,得到的是最低位到最高位呀,可我们要打印的是最高位到最低位,那此时我们可能还需要再创建一个循环来颠倒打印的顺序,由此看来常规思路解题确实要麻烦。
那么接下来我们用递归的思想来看看这题如何解答:
因为递归函数是可以多次进行,然后反向打印的。那我们可以让函数一直/10,直到变成个位数,再把递归函数存储的数据依次打印出来
#include <stdio.h>
void Print(int a)
{
if (a > 9)
{
Print(a / 10);
}
printf("%d ", a % 10);
}
int main()
{
int a;
scanf("%d", &a);
Print(a);
return 0;
}
2.递归函数的缺点
虽然递归函数能使很多问题简化,代码简化,但也是一把双刃剑。
- 递归函数的解题方法一般比较难想。
- 递归函数多次调用函数会使用更多的栈空间,有时会降低运算的效率。
- 如果需要运算的数据循环次数过多,容易导致堆栈溢出错误。
我们来做一道例题,直观的感受递归函数的缺点,和有些情况下它会一定程度上对程序员思想禁锢(因为敲起来比较简单,有些人做什么题都想着用递归函数)
问题:求第n个斐波那契数
斐波那契数就是像1 1 2 3 5 8 13 21 34 55...这样的数列,第n个数等于n-1个数加第n-2个数。学习过递归函数,读完题后觉得求第n个数只需要一个一个往前递归就好了呀,我们下意识的就想用递归函数去解题。那我们来打代码看看。
#include <stdio.h>
int Print(int a)
{
if (a <= 2)
return 1;
else
return Print(a - 1) + Print(a - 2);
}
int main()
{
int a;
scanf("%d", &a);
int m = Print(a);
printf("%d", m);
return 0;
}
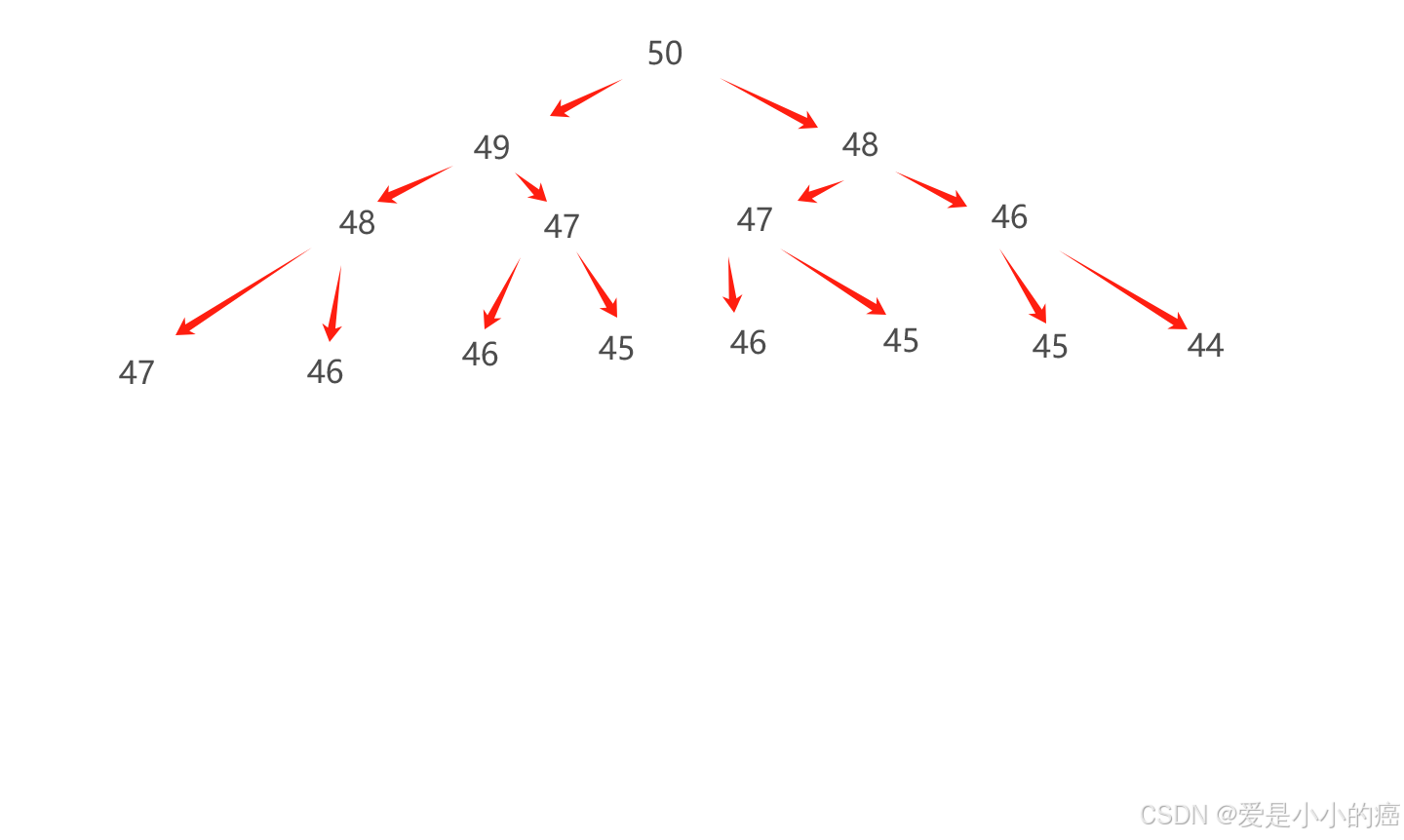
四、递归的练习(汉诺塔问题)
汉诺塔的游戏规则:
1、有三根相邻的柱子,标号为A,B,C。
2、A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。
3、你需要把所有盘子移动到柱子C,并且必须还是金字塔状。
如果只有一个圆盘,只需要移动一次就好了。A->C(1步)
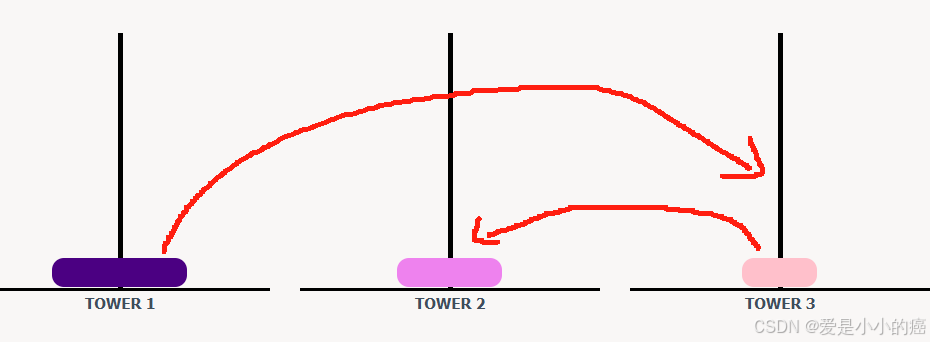
如果有两个圆盘,就需要借助第二个柱子(解题的关键),先把小的存放在第二个,把大的放第三个,再把小的放第一个。A->B A->C B->C(3步)
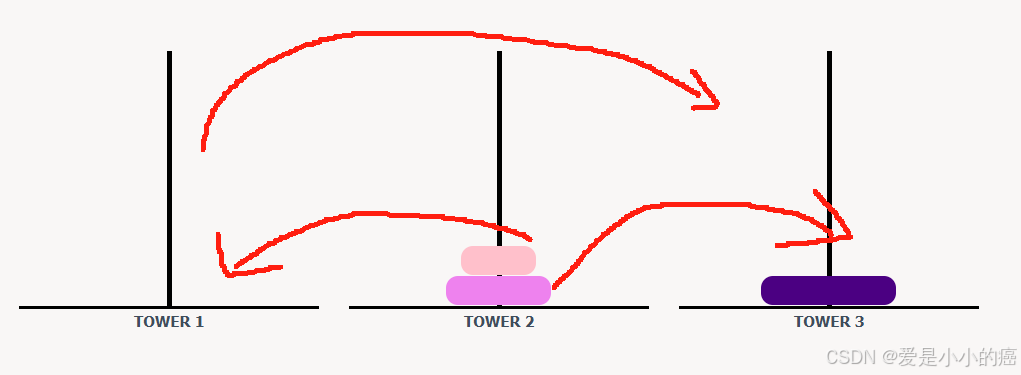
如果有三个圆盘,就比较麻烦了,
一共需要移动:A->C A->B C->B A->C B->A B->C A->C(7步)
(次数是2的n次方-1)
虽然越来越复杂,但都是一个思想:先把除了最大的盘子,都放到第二个柱,然后把最大的盘子放到第三个柱,再把除了第二大的盘子,其余的都放在第一个柱,把第二大的盘放第三个柱,依次循环往复。发现了吧!这也是一个递归函数!
#include <stdio.h>
int i;
void move(char ta1, char ta3)
{
printf("%c->%c ", ta1, ta3);//用于移动最后剩下的一个盘子
}
int Hanoi(char ta1, char ta2, char ta3, int n)
{
i++;//计算移动了多少次
if (n == 1)
{
move(ta1, ta3);
}
else
{
Hanoi(ta1, ta3, ta2, n - 1);//先将除最下面的盘子借助第三个塔移到第二个塔
move(ta1, ta3);//移动最后一个盘子去第三个塔
Hanoi(ta2, ta1, ta3, n - 1);//将第二个塔上剩下的盘子借助第一个移到第三个
}
return i;
}
int main()
{
int a;
char A = 'A';
char B = 'B';
char C = 'C';
scanf("%d", &a);
Hanoi(A, B, C, a);
printf("\n%d", i);
return 0;
}运行结果展示: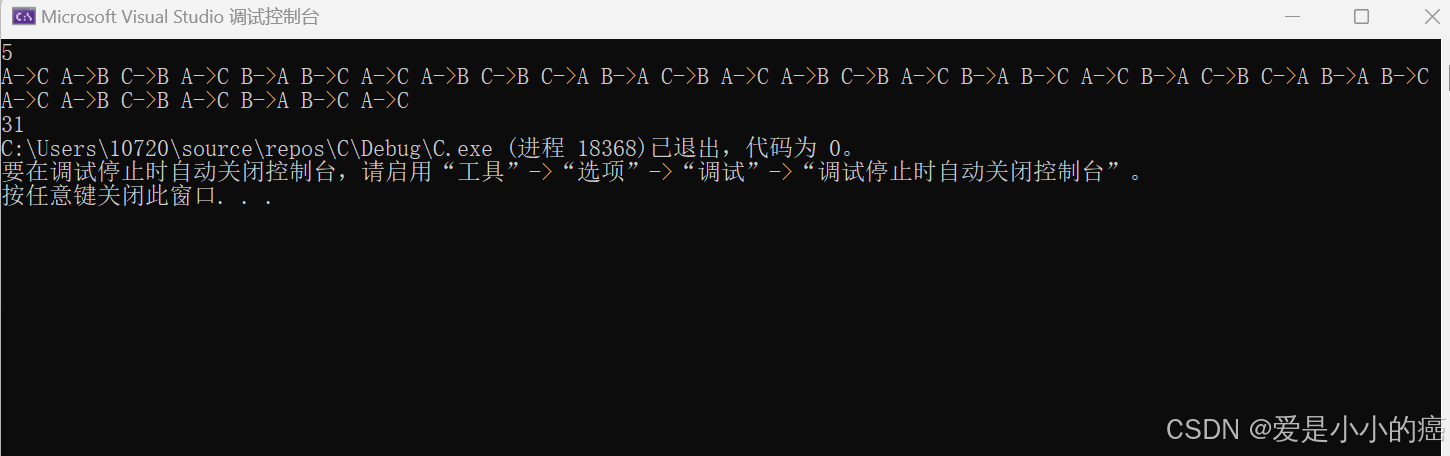
关于递归函数相关的知识,今天就先分享到这里啦,我们下次再见!!!