本文翻译至Neural Networks in PyMC3 estimated with Variational Inference
(c) 2016 by Thomas Wiecki。
当前机器学习趋势
当前机器学习界的三大趋势:概率编程,深度学习,大数据,在概率编程(Probabilistic Programming, PP)中,许多创新让变分推理(Variational Inference)更加广泛。本文说明了如何使用PyMC3中变分推理来拟合一个简单的贝叶斯神经网络。同时也讨论了如何架起概率编程和深度学习的桥梁。
大规模概率编程
概率编程允许我们非常灵活的创造自己的概率模型,这主要涉及洞察数据和从数据中学习。这种方法本质上是属于贝叶斯方法,因此我们可以指定先验信息来约束模型,最终以后验分布的形式对不确定性进行估计。使用MCMC采样算法 可以从后验中采样来对模型进行灵活的估计,但是采样算法的缺点是速度很慢,特别对于高维模型。因此变分推理 Variational Inference算法孕育而生,变分推理与MCMC有着相似的灵活性的同时大大提高了速度。变分推理用对后验分布的拟合取代对后验的采样,将一个采样问题转换位最优化问题。在PyMC3、Stan和Edward中实现的涉及的变分推理算法主要是自动微分变分推理(Automatic Differentation Variational Inference, ADVI)。
不幸的是,对于传统的机器学习问题,如分类和(非线性)回归,相比于集成学习方法(如随机森林和梯度提升回归树),概率编程往往退居二位(由于准确性和扩展性的不足).
深度学习
从统计学角度看,神经网络是很好的非线性函数进行方法和表示学习方法。在广为人知的分类领域,已经发展出了使用自编码器的无监督学习,然而其有效工作背后的统计学原理尚不得而知。
在深度学习领域大量的创新是能够训练越来越复杂的模型,这取决于一下几个支柱:
* 速度:方面的GPU计算加快了编程开发速度。
* 软件:Theano 和 TensorFlow的框架的出现简化了模型的建立和优化。
* 学习算法:使用随机梯度下降在部分数据集上进行训练让模型得以对大规模的数据集进行训练。同时又有如drop-out等技术防止过拟合的发生。
* 架构:大量创新在于改变了输入层(如卷积神经网络convolutional neural net,CNN),或者对输出层的改变(如混合密度网络Mixture Density Networks,MDN)。
架起深度学习和概率编程的桥梁
一方面,概率编程允许我们建立小而专注的模型深入了解数据;另一方面,深度学习可以运用许多启发式的方法来训来拿大而复杂的模型,获得较好的预测效果。最近在变分推理上的创新允许概率编程处理复杂模型和大数据量。结合这两种方法可以获得一些新的创新,这篇博客中有一些新的思路。
当能够把概率编程应用到更加广泛的问题上,这种结合(深度学习和概率编程的结合)将给深度学习带来更加巨大的创新。下面是一些思路:
预测的不确定性 :贝叶斯神经网络给出了预测中的不确定性。作者认为不确定性是一个在深度学习中尚未被从分利用的信息,相反在现实世界中不确定性有着相当重要的应用。但是在训练中,不确定性是非常有用的,比如可以专门针对不确定的样本进行训练。
表示的不确定性:在对权值的估计中也存在着不确定性,这种不确定性可以对网络学习出来的表示模型的稳健性进行评估。
正则化先验:由于权重系数通常采用高斯先验,因此权重通常进行L2正则化来防止过拟合。但是可以考虑采用其他先验(比如spike-and-slab)来增加稀疏性(这有点类似与使用L1范数)。
迁移学习和知情先验:可以将知情先验的信息加入到预训练网络(如GoogLeNet)的权值上进行迁移学习。
分层神经网络:概率编程的强大之处在于支持分层建模,这允许将数据子集的结果汇集到一起。在分层数据集上应用神经网络,可以在使用全局先验的同时对数据子集训练独立网络。例如要训练一个汽车照片的分类网络,可以训练一个分层子网络只对某一厂家的汽车进行分类。由于同一个厂家的汽车有一些共性,这样对于同一品牌的汽车训练一个独立网络的话可以利用这些共性。与此同时,由于这些独立网络都连接到更高层的网络上,这些子网络之间可以交换一些所有品牌公有的特征的信息。有趣的是,网络中的不同层次可以识别不同层次的数据模式,比如在前期层次中可以是别处一些线条,在高层的子网络中可以识别出一些高级的模式。
其他混合结构:可以混合各种神经网络模型。例如贝叶斯非参数模型可以通过改变隐层大小和形状来改变网络结构,当然这需要大量的超参数优化和领域知识。
PyMC3中的贝叶斯深网络
生成数据
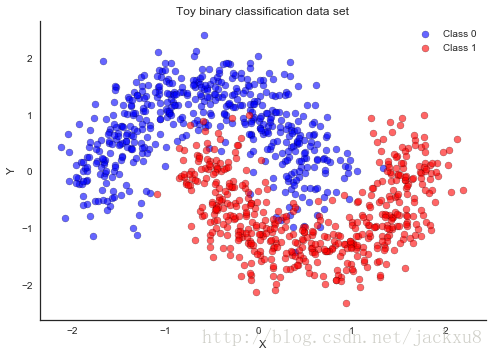
产生一个简单的线性不可分的二分类问题的模拟数据。
%matplotlib inline
import pymc3 as pm
import theano.tensor as T
import theano
import sklearn
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('white')
from sklearn import datasets
from sklearn.preprocessing import scale
from sklearn.cross_validation import train_test_split
from sklearn.datasets import make_moons/Users/xujie/.pyenv/versions/anaconda3-4.3.1/lib/python3.6/site-packages/sklearn/cross_validation.py:44: DeprecationWarning: This module was deprecated in version 0.18 in favor of the model_selection module into which all the refactored classes and functions are moved. Also note that the interface of the new CV iterators are different from that of this module. This module will be removed in 0.20.
"This module will be removed in 0.20.", DeprecationWarning)
X, Y = make_moons(noise=0.2, random_state=0, n_samples=1000)
X = scale(X)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.5)fig, ax = plt.subplots()
ax.scatter(X[Y==0, 0], X[Y==0, 1], color='b',edgecolors='k',alpha=0.6, label='Class 0')
ax.scatter(X[Y==1, 0], X[Y==1, 1], color='r',edgecolors='k',alpha=0.6, label='Class 1')
sns.despine(); ax.legend()
ax.set(xlabel='X', ylabel='Y', title='Toy binary classification data set');模型定义
神经网络的基础单元是感知器,和逻辑回归中的类似。将感知器并行排列然后堆叠起来获得隐层。这里使用2个隐层,每层有5个神经元。使用正态分布来正则化权重。
ann_input = theano.shared(X_train)
ann_output = theano.shared(Y_train)
n_hidden = 5
# Initialize random weights between each layer
init_1 = np.random.randn(X.shape[1], n_hidden)
init_2 = np.random.randn(n_hidden, n_hidden)
init_out = np.random.randn(n_hidden)
with pm.Model() as neural_network:
# Weights from input to hidden layer
weights_in_1 = pm.Normal('w_in_1', 0, sd=1,
shape=(X.shape[1], n_hidden),
testval=init_1)
# Weights from 1st to 2nd layer
weights_1_2 = pm.Normal('w_1_2', 0, sd=1,
shape=(n_hidden, n_hidden),
testval=init_2)
# Weights from hidden layer to output
weights_2_out = pm.Normal('w_2_out', 0, sd=1,
shape=(n_hidden,),
testval=init_out)
# Build neural-network using tanh activation function
act_1 = T.tanh(T.dot(ann_input, weights_in_1))
act_2 = T.tanh(T.dot(act_1, weights_1_2))
act_out = T.nnet.sigmoid(T.dot(act_2, weights_2_out))
# Binary classification -> Bernoulli likelihood
out = pm.Bernoulli('out',
act_out,
observed=ann_output)/Users/xujie/.pyenv/versions/anaconda3-4.3.1/lib/python3.6/site-packages/theano/tensor/basic.py:2146: UserWarning: theano.tensor.round() changed its default from `half_away_from_zero` to `half_to_even` to have the same default as NumPy. Use the Theano flag `warn.round=False` to disable this warning.
"theano.tensor.round() changed its default from"
变分推理:缩放模型的复杂性
现在可以使用MCMC采样器(如NUTS)进行采样将获得不错的效果,但是这会非常缓慢。这里使用全新的ADVI变分推理算法,更加快速,对模型复杂度的适应性也更好。但是,这是均值近似,因此忽略后验中的相关性。
%%time
with neural_network:
# Run ADVI which returns posterior means, standard deviations, and the evidence lower bound (ELBO)
v_params = pm.variational.advi(n=50000)Average ELBO = -151.63: 100%|██████████| 50000/50000 [00:13<00:00, 3790.27it/s]
Finished [100%]: Average ELBO = -136.89
CPU times: user 15.5 s, sys: 695 ms, total: 16.1 s
Wall time: 18 s
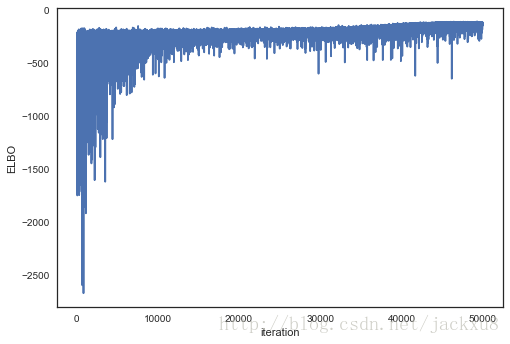
画出目标函数(ELBO)可以看出随着优化的进行,效果主见提升。
plt.plot(v_params.elbo_vals);
plt.ylabel('ELBO');
plt.xlabel('iteration');为了观察方便,这里使用sample_vp()对后验进行采样(这个函数只是对正态分布进行采样,因此和MCMC不一样)。
with neural_network:
trace = pm.variational.sample_vp(v_params, draws=5000)100%|██████████| 5000/5000 [00:00<00:00, 10687.44it/s]
这里完成了模型训练,然后使用posterior predictive check (PPC)对排除在外的数据点进行预测。使用sample_ppc()从后验中生成新数据(从变分估计中采样)。
# Replace shared variables with testing set
ann_input.set_value(X_test)
ann_output.set_value(Y_test)
# Creater posterior predictive samples
ppc = pm.sample_ppc(trace, model=neural_network, samples=500)
# Use probability of > 0.5 to assume prediction of class 1
pred = ppc['out'].mean(axis=0) > 0.5100%|██████████| 500/500 [00:03<00:00, 139.67it/s]
fig, ax = plt.subplots()
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1], color='b',edgecolors='k',alpha=0.6)
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r',edgecolors='k',alpha=0.6)
sns.despine()
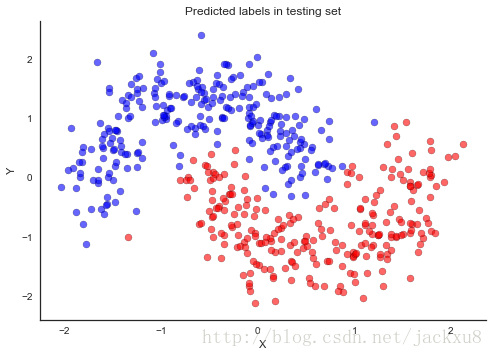
ax.set(title='Predicted labels in testing set', xlabel='X', ylabel='Y');print('Accuracy = {}%'.format((Y_test == pred).mean() * 100))Accuracy = 95.6%
分类器分析
为了分析这个分类器的结果,多整个输入空间上的网络输出做出评估。
grid = np.mgrid[-3:3:100j,-3:3:100j]
grid_2d = grid.reshape(2, -1).T
dummy_out = np.ones(grid.shape[1], dtype=np.int8)ann_input.set_value(grid_2d)
ann_output.set_value(dummy_out)
# 对后验估计进行采样
ppc = pm.sample_ppc(trace, model=neural_network, samples=500)100%|██████████| 500/500 [00:04<00:00, 101.43it/s]
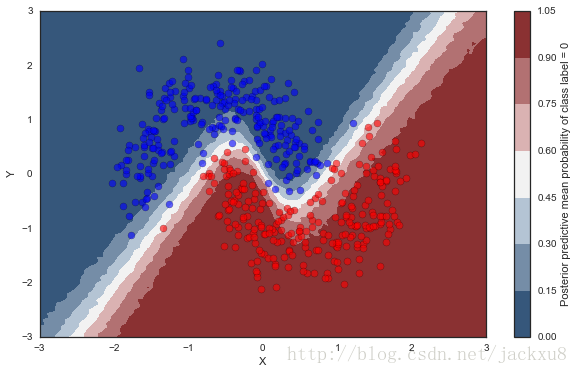
绘制预测平面如下
cmap = sns.diverging_palette(250, 12, s=85, l=25, as_cmap=True)
fig, ax = plt.subplots(figsize=(10, 6))
contour = ax.contourf(*grid, ppc['out'].mean(axis=0).reshape(100, 100), cmap=cmap)
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1], color='b', edgecolors='k',alpha=0.6)
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r', edgecolors='k',alpha=0.6)
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y');
cbar.ax.set_ylabel('Posterior predictive mean probability of class label = 0');预测中的不确定性
目前未知,这些工作都可以在非贝叶斯神经网路上完成。每个类别的后验均值可以用极大似然估计给出。然而,贝叶斯神经网络还可以给出后验估计的标准差,来评价后验中的不确定性。
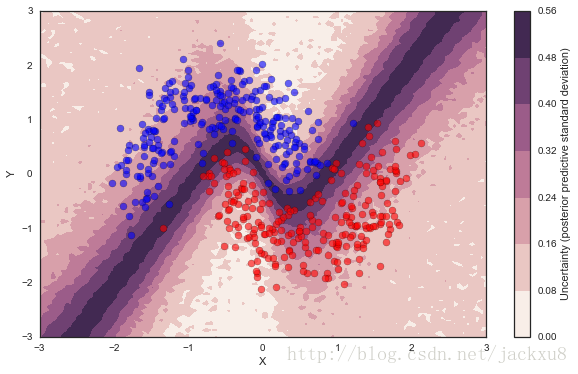
cmap = sns.cubehelix_palette(light=1, as_cmap=True)
fig, ax = plt.subplots(figsize=(10, 6))
contour = ax.contourf(*grid, ppc['out'].std(axis=0).reshape(100, 100), cmap=cmap)
ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1], color='b', edgecolors='k',alpha=0.6)
ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r', edgecolors='k',alpha=0.6)
cbar = plt.colorbar(contour, ax=ax)
_ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y');
cbar.ax.set_ylabel('Uncertainty (posterior predictive standard deviation)');可以看出,在越接近决策边界的地方,预测的不确定性越高。而预测结果与不确定性相关联分析是许多应用领域的重要因素,比如医学检测。为了更高的准确性,可以让模型在不确定性高的地方进行更多的采样。
微批AVDI(Mini-batch AVDI):可扩展数据大小
此前,都是在所有数据上一次性训练模型。这样的训练方式对于数据集的大小不可扩展。然而可以在一小批数据上(mini-batch of data)进行训练(随机梯度下降),可以避免局部最小并获得更快的收敛。
from six.moves import zip
# Set back to original data to retrain
ann_input.set_value(X_train)
ann_output.set_value(Y_train)
# Tensors and RV that will be using mini-batches
minibatch_tensors = [ann_input, ann_output]
minibatch_RVs = [out]
# Generator that returns mini-batches in each iteration
def create_minibatch(data):
rng = np.random.RandomState(0)
while True:
# Return random data samples of set size 100 each iteration
ixs = rng.randint(len(data), size=50)
yield data[ixs]
minibatches = zip(
create_minibatch(X_train),
create_minibatch(Y_train),
)
total_size = len(Y_train)%%time
with neural_network:
# Run advi_minibatch
v_params = pm.variational.advi_minibatch(
n=50000, minibatch_tensors=minibatch_tensors,
minibatch_RVs=minibatch_RVs, minibatches=minibatches,
total_size=total_size, learning_rate=1e-2, epsilon=1.0
)Average ELBO = -123.12: 100%|██████████| 50000/50000 [00:16<00:00, 3043.69it/s]
Finished minibatch ADVI: ELBO = -121.76
CPU times: user 20.5 s, sys: 371 ms, total: 20.9 s
Wall time: 23.9 s
with neural_network:
trace = pm.variational.sample_vp(v_params, draws=5000)100%|██████████| 5000/5000 [00:00<00:00, 9914.64it/s]
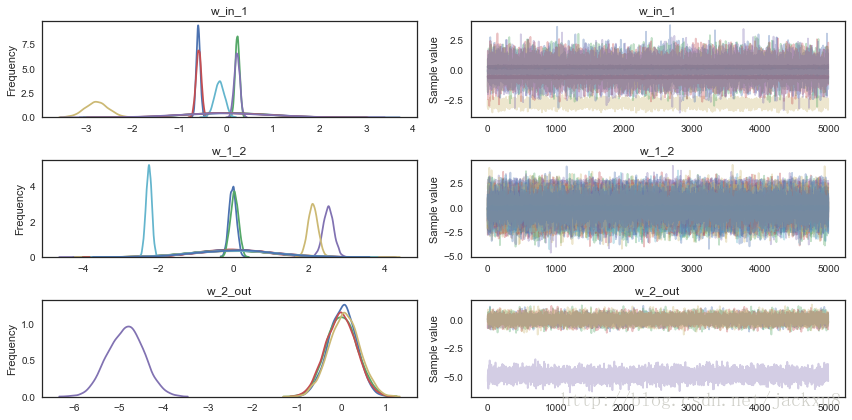
mini-batch方式的运行时间更长,但是收敛更快。
pm.traceplot(trace);