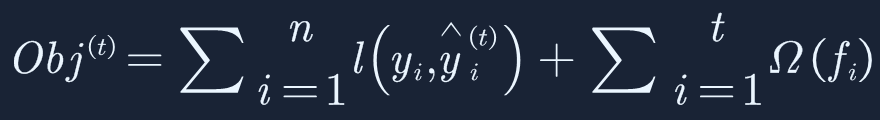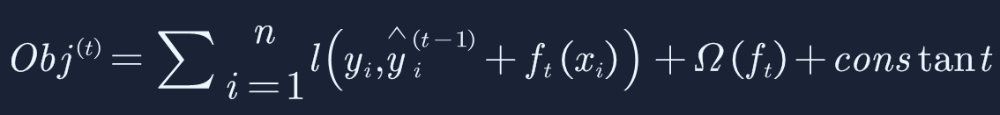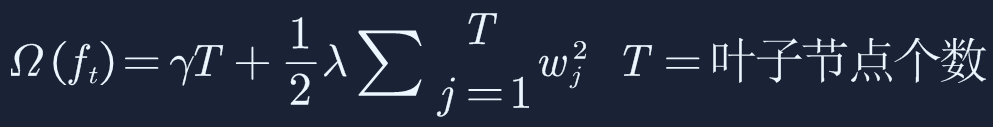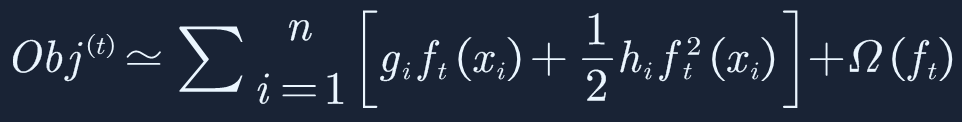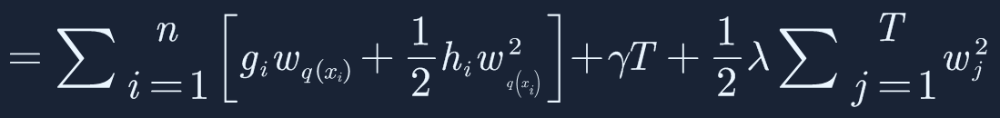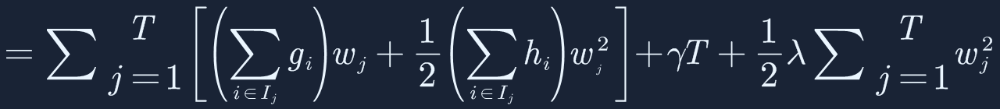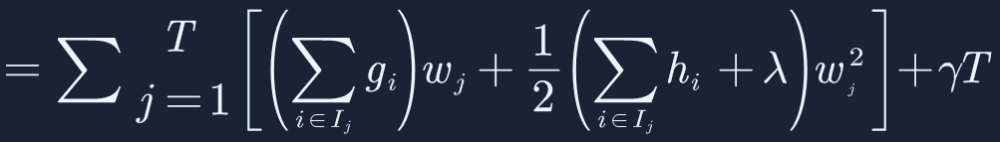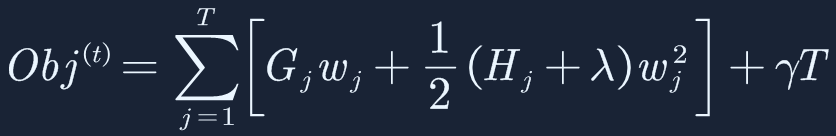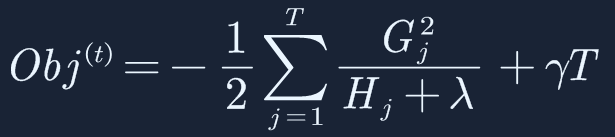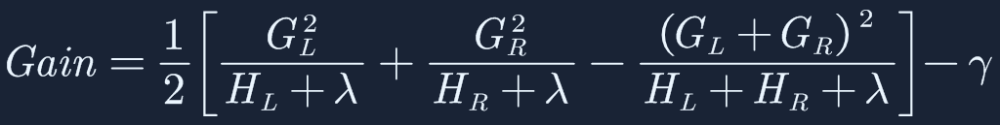转自XGBoost
XGBoost
XGBoost全名叫(eXtreme Gradient Boosting)极端梯度提升,或者叫极值梯度提升算法,在各种数据竞赛中大放异彩,其效果显著。它是大规模并行boosted tree的工具,可以说它是目前最好最快的boosted tree工具包。XGBoost 所应用的算法就是 GBDT的改进,既可以用于分类也可以用于回归问题中。GBDT上一节已经介绍,xgboost扩展和改进了GDBT,xgboost算法更快,准确率等性能也相对高一些。学习Xgboost之前,需要了解决策树,集成学习,GBDT等算法的概念(参考以上章节),会帮助更好的去理解Xgboost。本文主要从以下几个方面介绍该算法模型:
其实XGBoost是在GBDT基础上的高效实现,可以说XGBoost是建立在GBDT算法基础上的模型,只是在算法和性能方面做了一些改善。对比原算法GBDT,XGBoost主要从下面三个方面做了优化:
(1)算法本身的优化:在算法的弱学习器模型选择上,目前GBDT只支持决策树,XGBoost可以支持很多其他的弱学习器。XGBoost在算法的损失函数上,除了本身的损失,还加上了正则化部分。在算法的优化方式上,GBDT的损失函数只对误差部分做负梯度(一阶泰勒)展开,而XGBoost损失函数对误差部分做二阶泰勒展开,更加准确。算法本身的优化后面会有详细介绍。
(2)算法运行效率的优化:对每个弱学习器,比如决策树建立的过程做并行处理,由于是串行树,这里的"并行"并不是对树的创建进行并行处理,而是对每个特征寻找最佳分裂点进行并行处理,我们都知道,对于连续型特征,决策树是通过贪婪算法寻找最佳分裂点,也就是对特征进行排序,从小到大依次判断最佳分裂点,找到合适的子树分裂特征和特征值。在并行选择之前,先对所有的特征的值进行排序分组,方便前面说的并行处理。对分组的特征,选择合适的分组大小,使用CPU缓存进行读取加速。将各个分组保存到多个硬盘以提高IO速度。
(3)算法健壮性的优化:对于缺失值的特征,通过枚举所有缺失值在当前节点是进入左子树还是右子树来决定缺失值的处理方式。算法本身加入了L1和L2正则化项,可以防止过拟合,泛化能力更强。
基本原理
如上文所介绍,XGBoost也是由多个弱分类器串行构成,不断的优化误差(残差)的串行模型,同时考虑了正则化的部分,XGBoost的目标函数最终如下:
从目标函数中可以看到,除了包含多个弱分类器之外,也考虑到了正则化部分Ω,它是由叶子节点和L2正则化共同组成,一是可以约束叶子节点防止过拟合,二是可以对权重w进行约束,同样也是为了防止过拟合,提高泛化能力。
公式推导
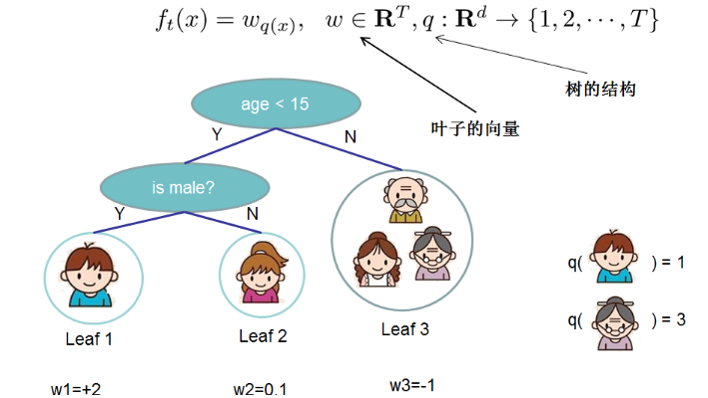
XGBoost是通过不断的优化误差(残差)来实现模型的训练,最终每个样本Xi的预测值会落到树的某个节点上,这里用W来表示最终的预测值,那么树中的每个叶子节点都会对应一个权重W,叶子节点内的样本共享这个权重W,然后用q(x)指代样本Xi对应的叶子节点,官方说q(x)是一个function(函数),这里的函数不是数学意义上的函数,而是用来标记每个样本Xi最终会落在树中的哪个叶子节点上,如下图所示,T代表的是该第t棵树总共有T个叶子节点,q代表样本落在了哪个叶子节点(leaf)上。事实上,公式的推导以及模型的训练,最终都是为了求解W,找到最优解,而XGBoost是串行树,同一个样本可能出现在不同的树上(考虑到样本可能采取随机抽样,所以不是出现在全部树上),因此该样本的最终预测为带有该样本的叶子节点权重之和,如果定义了学习率(后续会讲解),那就用叶子节点权重乘以学习率再求和,得到该样本的最终预测结果。公式如下:
下面举个例子来尝试说明权重W,假设我们有三个自变量,分别是(年龄,性别,使用电脑情况),因变量是预测每个人对电子游戏的喜好程度,这里明显是一个回归问题,假设小男孩的喜好程度是3,老爷爷的喜好程度是-0.5,根据XGBoost的模型训练(后续有公式推导),最终我们得到了两棵树,同时也得到了每棵树叶子节点的权重W(来自后续公式推导),我们可以看到小男孩在第一棵树的叶子节点上的权重是+2,在第二棵树上的权重是+0.9,不考虑学习率的情况下,总的权重是2.9,这已经非常接近真实值3了,所以整个XGBoost就是在求解最优W叶子节点权重。
目标损失函数的推导:
用泰勒展开来近似我们原来的目标:
一阶导数g和二阶导数h的定义如下:
根据泰勒展开公式,以及对一阶导数和二阶导数的定义,目标函数可以写成:
这里的第t棵回归树是根据前面的t-1棵回归树的残差得来的,相当于t-1棵树的值是已知的,因此
是一个常数,对目标函数的优化,可以省略掉常数部分,因此目标函数可以简化成如下:
根据上面的介绍,我们知道ft(xi)=wq(x),目标函数继续简化:
这里对目标函数做了一个转化,从样本统计的角度转化成从叶子节点的统计,这两种统计方式的结果会是完全一致,因为全部的样本都会落在最终的叶子节点上,这里只考虑第t棵树(XGBoost是一棵树接着一棵树的优化),假设第t棵树一共有10个叶子节点,样本量总共有100个,对这100个样本计算目标函数Obj,和对10个叶子节点算Obj是一样的,因为这100个数据样本最终都会落到这10个叶子节点上。j代表的就是第几个叶子节点,T是一共存在的叶子节点数,那我们知道不同的数据样本可能会落到不同的节点上面,所以用来表示哪些样本X落到了 j 这个叶子节点上。落到 j 叶子节点的样本共享权重wj,然后对 j 叶子节点内的样本计算其Σg 和Σh,目标函数继续简化:
这里对一阶导和二阶导单独表示:
目标函数继续简化:
基于目标函数对w进行求导,并令导数为0,可以得到w:
将w再带入到目标函数,最终目标函数为:
通过对目标函数的优化,在创建树时,节点进行分裂时,目标就是寻找能够最大化的优化目标函数的串行树结构,从而可以确定每棵树的结构,以及叶子节点的权重。
分类器
我们在讲到GBDT时,提到了节点如何分割,以及是否有必要分割,以及分割后的c值,xgboost是根据一阶导数g和二阶导数h,通过迭代的方式生成基学习器,通过串行的方式生成强学习器,对于每一次节点的分割(左右子树分裂时),目标是最大程度的减少损失函数的损失,也就是我们期望最大化如下公式,也就是分裂后,左右子树的损失函数加在一起,一定大于不分裂前的损失函数,同时为了约束Gain,引入了超参数,用来限制损失函数减少的程度。XGBoost的分类器可以是基于树的结构(gbtree),也可以是基于线性的结构(gblinear),但一般还是选择树结构,线性结构不是很好。
XGBoost并行计算
对于树结构的模型来说,性能方面的问题主要是由寻找分裂节点所造成的,对于一个连续型特征而言,如何寻找最佳分裂点呢?通常会有贪心算法和近似算法。贪心法,从树深度0开始,每一节点都遍历所有的特征,比如年龄、性别等等,然后对于某个特征,先按照该特征里的值进行排序,然后逐个扫描该特征值进而确定最好的分割点,最后对所有特征进行分割后,我们选择所谓的增益Gain最高的那个特征。近似算法主要针对数据太大,不能直接进行计算而言的。基本思想是通过特征的统计分布(分位数),按照百分比确定一组候选分裂点,比如十分位数,每个分位作为一个候选分裂点,对于连续型变量通过遍历所有的候选分裂点来找到最佳分裂点。近似算法有两种版本:global variant和local variant。global variant在树初始化时就确定了候选切分点;local variant是在每次节点分裂后重新选出候选点。两种策略:全局策略和局部策略。在全局策略中,对每一个特征确定一个全局的候选分裂点集合,就不再改变;而在局部策略中,每一次分裂都要重选一次分裂点(重新对剩下的数据计算分位数等)。前者需要较大的分裂集合,后者可以小一点。对比补充候选集策略与分裂点数目对模型的影响,全局策略需要更细的分裂点才能和局部策略差不多。
针对上面的问题(寻找最佳分裂点),XGBoost提出了并行迭代的概念,也就是说可以通过多线程或分布式的方式来寻找最佳分裂点,而这种并行方式并不会造成任何树结构的变化,同时,对训练的每个特征排序并且以块的的结构存储在内存中,方便后面迭代重复使用,减少计算量。计算量的减少参见上面算法流程总结,首先默认所有的样本都在右子树,然后从小到大迭代,依次放入左子树,并寻找最优的分裂点。这样做可以减少很多不必要的比较。
参数选择
'booster':'gbtree','gblinear'
'n_estimator': 弱学习器的数量
'objective': 'multi:softmax', 多分类的问题,默认是二分类
'num_class':10, 类别数,与 multi:softmax 并用
'gamma':损失下降多少才进行分裂(上面提到的Gain中的超参数γ)
'max_depth':12, 构建树的深度,越大越容易过拟合
'lambda':2, 控制模型复杂度的权重值的L2正则化项参数,参数越大,模型越不容易过拟合。
'alpha':2, 控制模型复杂度的权重值的L1正则化项参数,参数越大,模型越不容易过拟合。
'subsample':0.7, 随机采样训练样本
'colsample_bytree':0.7, 生成树时进行的列采样
'scale_pos_weight' : 控制正负样本权重平衡,对于非平衡数据非常有用,允许您为整个样本类(“正”类)提供权重,通常设置成sum(负样本数)/sum(正样本数)
'sample_weight': 参数允许您为每个训练样本指定不同的权重
(scale_pos_weight和sample_weight区别:这是对应于成本敏感学习的两种不同方法,如果您认为错误分类阳性示例(遗漏癌症患者)的成本与所有阳性示例相同(但比错误分类阴性示例的成本更高,例如,告诉某人他们患有癌症,而他们实际上没有),也就是说宁可错杀一万,也不放过一个的道理相同,正样本的预测更重要,不能放过任何可能患癌症的人,宁可误判,那么您可以通过scale_pos_weight为所有阳性示例指定一个权重。)
'min_child_weight':3, 孩子节点中最小的样本权重和。如果一个叶子节点的样本权重和小于min_child_weight则拆分过程结束,假设叶子节点的权重是0.01,若参数设置成1,则这个节点的样本数最少需要100个样本,本质上来说,这个参数其实是在控制叶子上所需要的最小样本量,这个参数用于避免过拟合。当它的值较大时,可以避免模型学习到局部的特殊样本,因为值越大包含的样本越多,那就不需要继续分裂下去了。但是如果这个值过高,会导致欠拟合
'silent':0 ,设置成1则没有运行信息输出,最好是设置为0
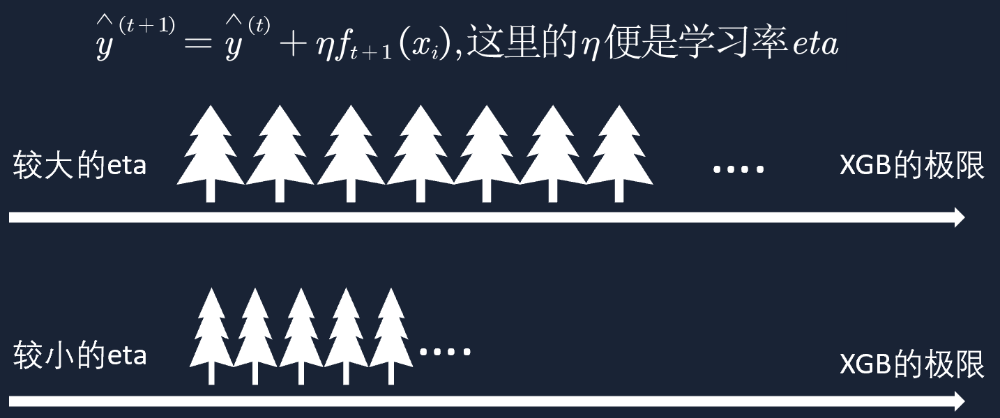
'eta': 0.007, 如同学习率,在每次迭代一棵树的时候对每个叶子结点的权重乘上一个缩减系数,使每棵树的影响不会过大,并且给后面的树留下更大的空间优化。不同的树,叶子节点的权重不同,叶子节点的数量也不同,在对某个样本计算对应的叶子节点权重求和时,权重都会被缩减,这样可以创建更多的树进行优化。如图所示:
'seed':1000 随机种子,保证每次初始化的数据都相同
'nthread':7, cpu 线程数
测试代码:
from sklearn.datasets import make_classification
from xgboost import XGBClassifier
from sklearn.metrics import accuracy_score
X, y = make_classification(n_samples=1000, n_features=4,n_informative=2, n_redundant=0,random_state=0, shuffle=False)
main_model = XGBClassifier(n_estimators=50, colsample_bylevel=0.7,
random_state=0,
n_jobs=-1, max_depth=3, min_child_weight=1,
gamma=0.1, learning_rate=0.03, subsample=0.7, colsample_bytree=0.9,
reg_alpha=0.6, missing=-1, reg_lambda=1.5, verbosity=2)
model = main_model.fit(X, y)
y_pre = model.predict(X)
print(accuracy_score(y, y_pre))