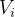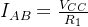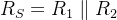一、戴维南定理
一个仅含有电压源、电流源及电阻的线性网络,从外部负载看,可以简单等效成一个电压源和电阻串联,用于分析复杂电路的输出阻抗、频率响应等
戴维南定理的基本步骤
1、断开负载电阻,端点记为AB,计算当前电源下AB两端的电压,即为等效电压源
2、短接所有电压源、开路所有电流源,在原负载电阻的位置放置电源,计算外部电路总电阻,即为等效内阻
3、将等效电压源与等效内阻串联,再与负载电阻串联构成回路,此时可以计算负载的电压及流过的电流
实际案例一
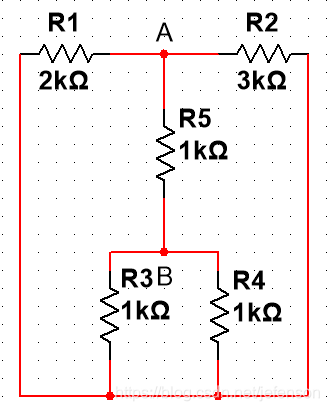
计算图1中R5上的电流
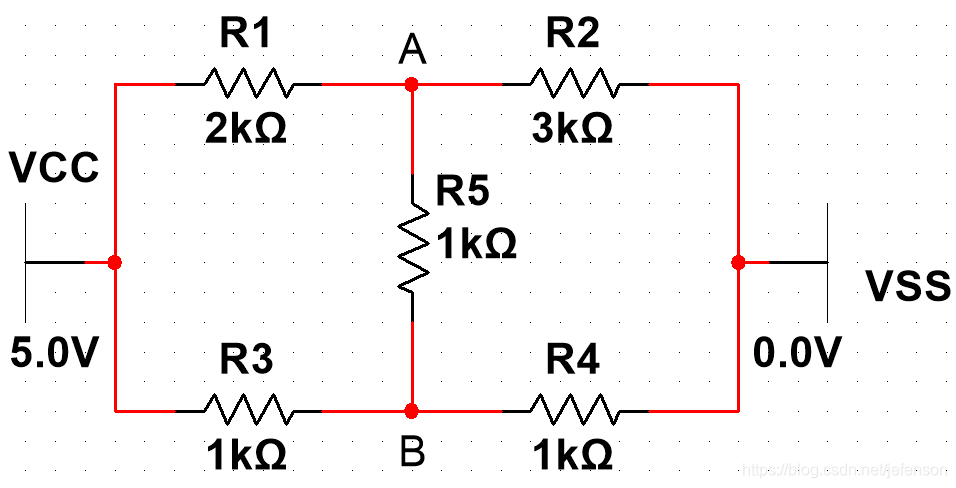
①将负载R5断开,计算AB两点电压
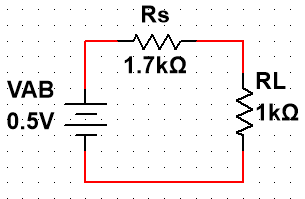
②短接VCC和VSS,电路变形后得到图2,其中R1和R2并联,R3和R4并联,
③绘制AB端的等效电路图,计算负载电流
若仅计算负载上的电压和电流,用戴维南定理比较简单,如果要计算其余电压和电流,则需要结合基尔霍夫定理。
实际案例二
如图4是音频功率放大器输入电路,PAOUTP和PAOUTN输出差分信号
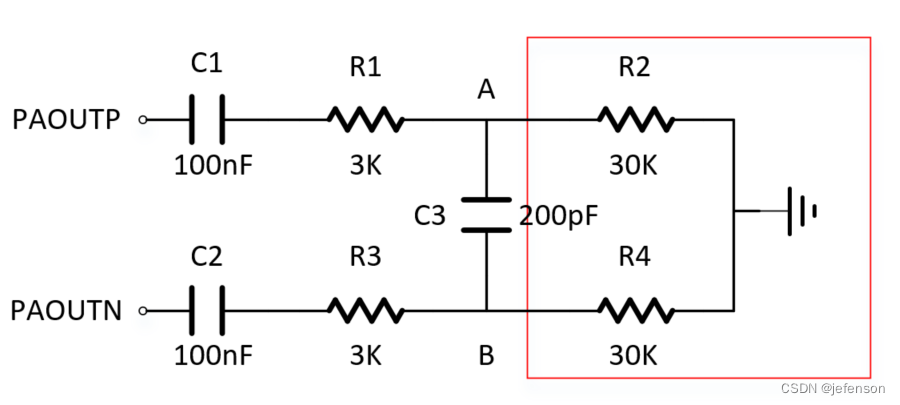
显然,C1与与R1、R2构成高通滤波器,截止频率是,约48Hz(C3容抗很大,视为开路),C3和R3、R4同理。当频率超过100KHz时,C3的容抗很小,AB两点视为短路,即C3与R1~R4构成低通滤波器
①将C3视为负载,负载开路,求AB两点电压(高频时,C1和C2视为短路)
②将PAOUTP和PAOUTN短路到地,电路变型,计算输出阻抗
③绘制AB端的等效电路,计算截止频率
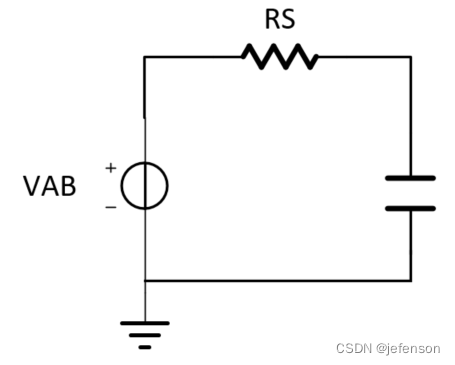
诺顿定理
一个仅含有电压源、电流源及电阻的线性网络,从外部负载看,可以简单等效成一个电流源和电阻并联,用于分析复杂电路的输出阻抗、频率响应等
诺顿定理的基本步骤
1、将负载电阻短路,端点记为AB,计算当前电源下AB间流过的电流,即为等效电流源
2、短接所有电压源、开路所有电流源,在原负载电阻的位置放置电源,计算外部电路总电阻,即为等效内阻
3、将等效电流源与等效内阻并联,再与负载电阻串联构成回路,此时可以计算负载的电压及流过的电流
实际案例一
计算图6中负载RL的电流
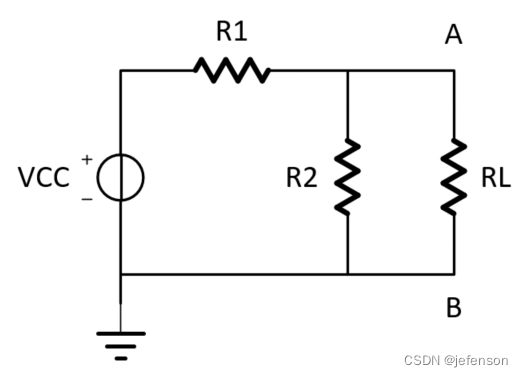
①负载RL短路,计算AB间流过的电路
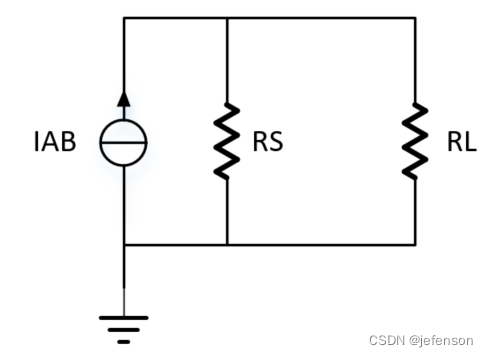
②将VCC短路,电路变型,计算输出阻抗
③绘制AB端的等效电路,计算负载电流
实际案例二
图8是共源极放大电路,负载与源极电阻串联,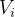
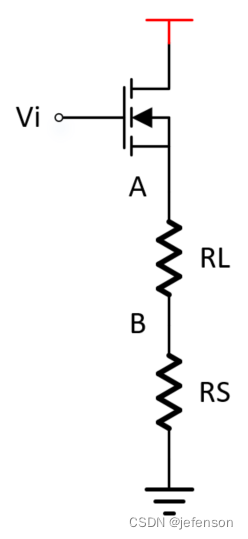
①将RL短路,计算AB间的电流
②将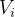
③绘制AB端的等效电路,计算负载电流
实际上,对图8应用戴维南定理也可以分析负载电流,此时AB间的电压等于