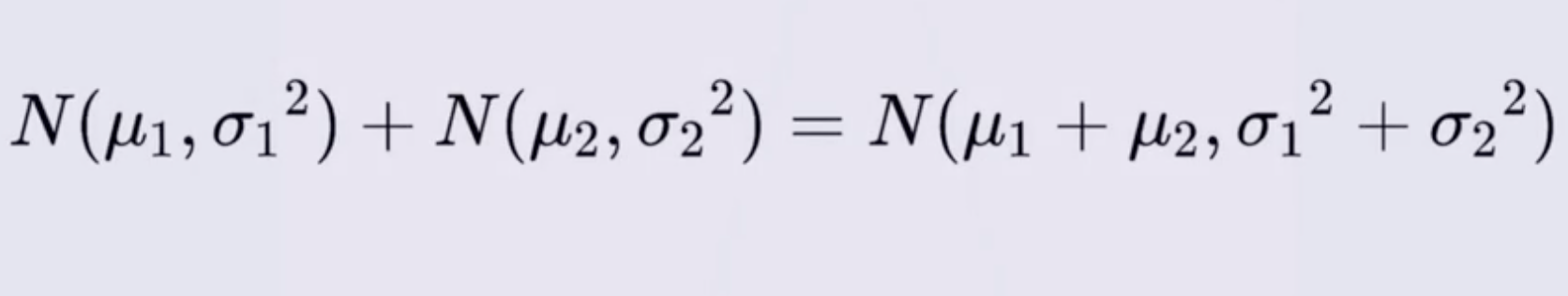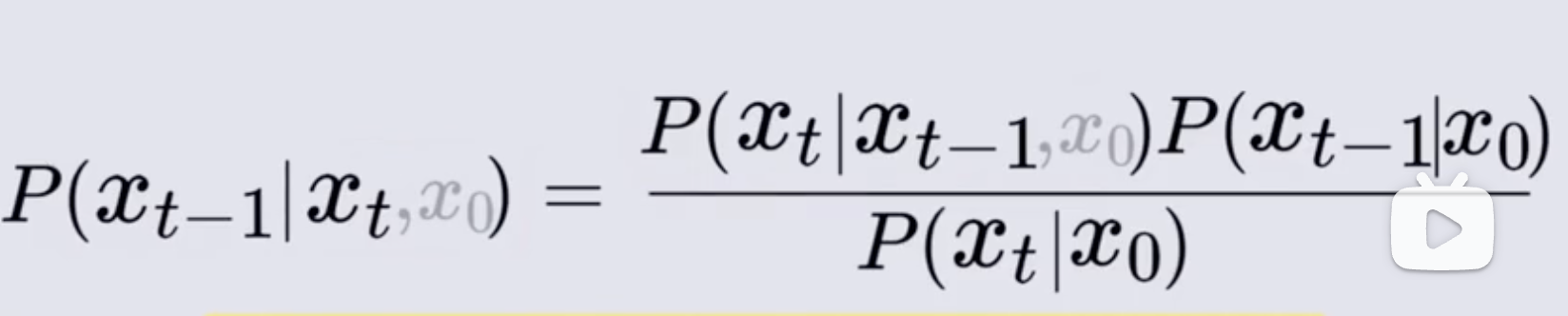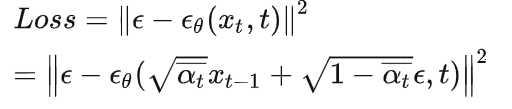论文:Denoising Diffusion Probabilistic Models
代码:https://github.com/hojonathanho/diffusion
stable diffusion 代码实现:https://github.com/CompVis/stable-diffusion/blob/main/ldm/models/diffusion/ddpm.py
出处:伯克利
时间:2020.06
数学基础知识
假设均值为 0,方差为 1 的高斯分布,则对应的噪声示例如下,就是在 0 附近分布的一些点
一、背景
扩散模型是一种用于描述系统中扩散过程的数学模型。扩散过程包括传播、渗透、传输等等。例如,在化学中,扩散模型可以用来描述分子之间的扩散运动。在社会学中,扩散模型可以用来描述信息、想法或行为在人群之间的传播。在物理学中气体分子从高浓度区域扩散到低浓度区域,这与由于噪声的干扰而导致的信息丢失是相似的。所以通过引入噪声,然后尝试通过去噪来生成图像。在一段时间内通过多次迭代,模型每次在给定一些噪声输入的情况下学习生成新图像。
即图像生成任务就是模拟分子扩散的过程,给图像中逐步加入噪声,最终变成一个看不出原本图像分布的噪声分布,然后通过逆向预测噪声来去噪的过程来进行图像生成。
在 DDPM 之前呢,其实在 2015 年就有利用扩散模型的思想来做图像生成的尝试了,但没有很好的效果
一般的思路还是两个过程,前向扩散和反向去噪:
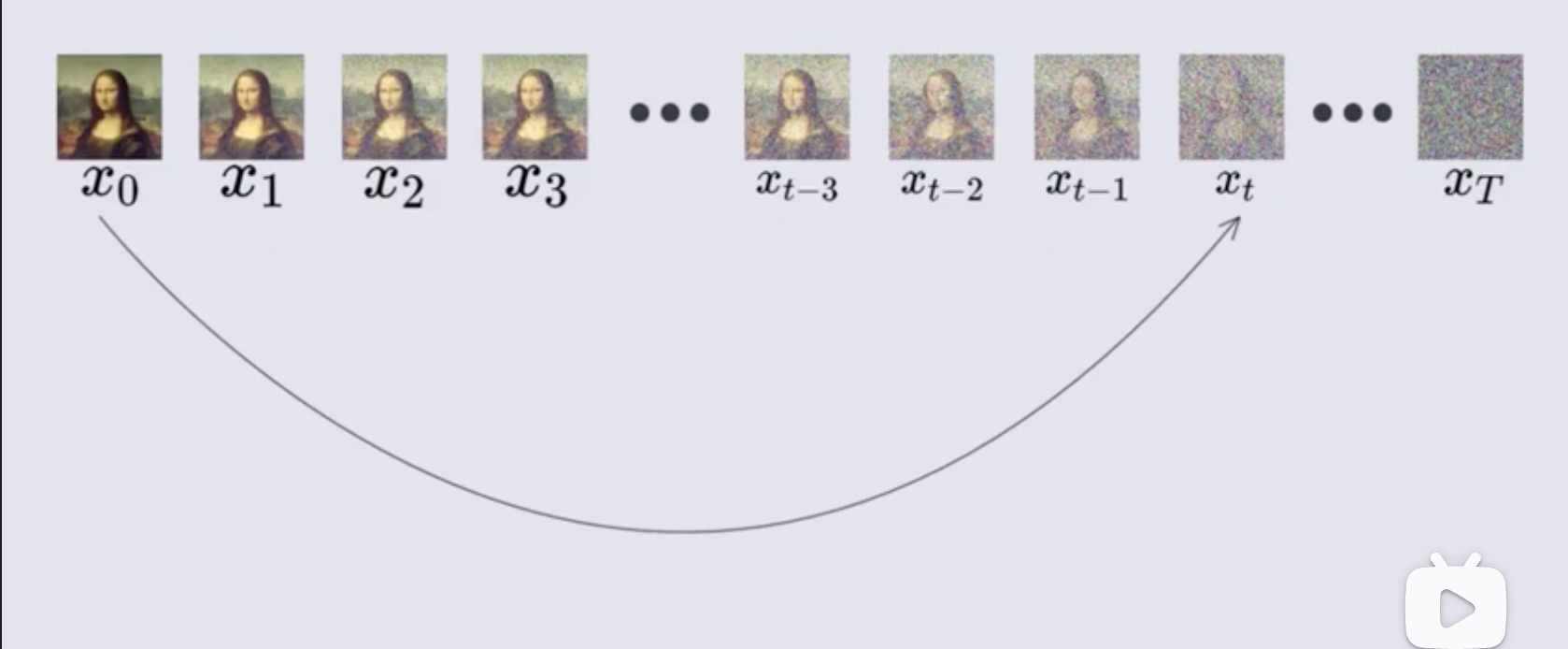
- 前向扩散:通过 t 次(t 可能很多,1000 次)的噪声添加,每次添加很小的随机噪声,逐步将输入图像加噪成一个正态分布,图片就变成了一个各向同性噪声
- 反向去噪:通过 t 次反向预测进行噪声去除,反向去噪的过程一般使用类似 U-Net 的结构,每次 t 到 t-1 状态的预测都是使用 U-Net encoder 先把图像压缩,decoder 再把图像恢复,U-Net 的输出是预测的图片,注意这里是图片,所以约是比较复杂的(U-Net 的参数是共享的)
DDPM 做了什么改进才把扩散模型的效果拉起来了呢:U-Net 不预测图片了,只预测本次添加的噪声
DDPM 是如何改的:
- U-Net 的输入不只是 Xt 时刻的图片了,还有一个 time embedding(可以看做类似 position embedding 的东西),也是一个向量,可以直接加,也可以直接拼接到输入图片特征上
- 为什么要引入 time embedding :反向扩展过程中,刚开始的时候希望 U-Net 能够先生成一些大概轮廓,粗糙的特征,不需要很清晰,随着扩展模型一点点往前走,到后面的时候希望模型能学习一些细节的特征。但 U-Net 模型是共享参数的,所以需要 time embedding 来提醒模型现在走到哪一步了,现在这个输出是要粗糙还是细致等等,所以 time embedding 还是很有用的
- loss:既然预测的是噪声,所以 loss 就是已知的噪声和预测的噪声的差值,而且前向过程添加的噪声是已知的,预测的噪声是 U-Net 的输出
- DDPM 还有一个贡献,因为一般如果要预测一个正态分布呢,只要学习均值和方差就可以了,其实进一步,只要预测均值就可以了,方差使用一个常数就能达到很好的效果,方差不用学了,再次降低了难度。DPPM 工作的很好了,能使用扩散模型来生成很好的图片了。
DDPM 是很多扩散模型的基础,其通过前向扩散和逆向去噪来实现对噪声的估计,从而将受噪声污染的图像复原。
重参数化:
- 在高斯分布 N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2) 上采样是一个随机过程,不能进行反向传播
- 所以可以通过重参数化来解决,先从标准正态分布 ϵ \epsilon ϵ ~ N ( 0 , 1 ) N(0,1) N(0,1) 上采样,然后乘以标准差,加上均值即可,也就是 σ × ϵ + μ \sigma \times \epsilon + \mu σ×ϵ+μ,将随机性转移到 ϵ \epsilon ϵ 上
二、DDPM 主要过程
2.1 前向扩散过程
前向扩散的实际操作就是给定一张图
x
0
x_0
x0,图片是有三个通道 RGB 的,都是 [0,255] 之间的数值,首先要将像素值归一化映射到 [-1,1] 之间,然后通过在标准正态分布 N(0,1) 中随机采样生成一张同样大小的噪声图片,噪声也是 3 通道的。然后将噪声和图片的对应位置上进行加权求和,加权求和的方式如下:
β
×
ϵ
+
1
−
β
×
x
\sqrt \beta \times \epsilon+\sqrt{1-\beta}\times x
β×ϵ+1−β×x
- x x x:输入图像
- ϵ ∼ N ( 0 , 1 ) \epsilon \sim N(0, 1) ϵ∼N(0,1):是添加的高斯噪声
- β \beta β:是一个权重参数,且 ( β ) 2 + ( 1 − β ) 2 = 1 (\sqrt \beta)^2 + (\sqrt {1-\beta})^2=1 (β)2+(1−β)2=1 永远成立,在前向扩展的过程中, β \beta β 也会越来越大,刚开始的 β \beta β 是比较小的,随着 β \beta β 的增大,噪声所占的比例会越来越大,可以大致看成从 0 到 1 逐步递增。如下图所示,所以可以用一个公式来表达前一时刻和后一时刻的关系。 x t = β t × ϵ t + 1 − β t × x t − 1 x_t=\sqrt {\beta_t} \times \epsilon_t + \sqrt {1-{\beta_t}} \times x_{t-1} xt=βt×ϵt+1−βt×xt−1。
然后引入一个变量 α t = 1 − β t \alpha_t=1-\beta_t αt=1−βt,所以 x t = 1 − α t ϵ t + α t x t − 1 x_t= \sqrt{1-\alpha_t} \ \epsilon_{t}+\sqrt{\alpha_t}\ x_{t-1} xt=1−αt ϵt+αt xt−1,从这个公式中可以看出,可以从 x 0 x_0 x0 经过 t 次噪声添加,得到 x T x_T xT 的图像
所以能不能直接简化这个过程呢,直接从 x 0 x_0 x0 到 x T x_T xT,经过一系列证明后,结论是可以!
两个正态分布叠加后,仍然是正态分布,且有如下公式:
然后经过一系列推断和重参数化技巧,根据上面的公式的思路可以得到下面的公式,也就是可以通过一步过程来从 x 0 x_0 x0 得到 x t x_t xt:
x t = α ‾ t x 0 + 1 − α ‾ t ϵ x_t=\sqrt{\overline{\alpha}_t}\ x_0 + \sqrt{1-\overline{\alpha}_t} \ \epsilon xt=αt x0+1−αt ϵ
- α ‾ t = Π i = 1 t α i \overline{\alpha}_t=\Pi_{i=1}^t\ \alpha_i αt=Πi=1t αi,表示累乘,就是有多少次引入噪声的过程,就有多少个值乘到一起
- ϵ ∼ N ( 0 , 1 ) \epsilon \sim N(0, 1) ϵ∼N(0,1)
- 上面的公式可以直接由输入图像 x 0 x_0 x0 来生成最终的加噪结果
2.2 逆向去噪过程
逆向去噪的目标是从 x T x_T xT 得到 x 0 x_0 x0
我们已知从 x t − 1 x_{t-1} xt−1 到 x t x_t xt 是添加随机噪声得到的,所以可以看做一个随机过程,所以从 x t x_t xt 到 x t − 1 x_{t-1} xt−1 的过程也是一个随机过程,所以可以用贝叶斯公式来解决,也就是在给定 x t x_t xt 的情况下,求前一时刻 x t − 1 x_{t-1} xt−1 的概率,这里 P ( x t − 1 ) P(x_{t-1}) P(xt−1) 是在 x t − 1 x_{t-1} xt−1 时刻的概率,也就是从 x 0 x_0 x0 得到它的概率
所以都加上 x 0 x_0 x0 作为前提条件,实际上可以忽略,所以基于 x t x_t xt 来求 x t − 1 x_{t-1} xt−1 的概率分布的公式如下:
现在分别求式子中的每一项:
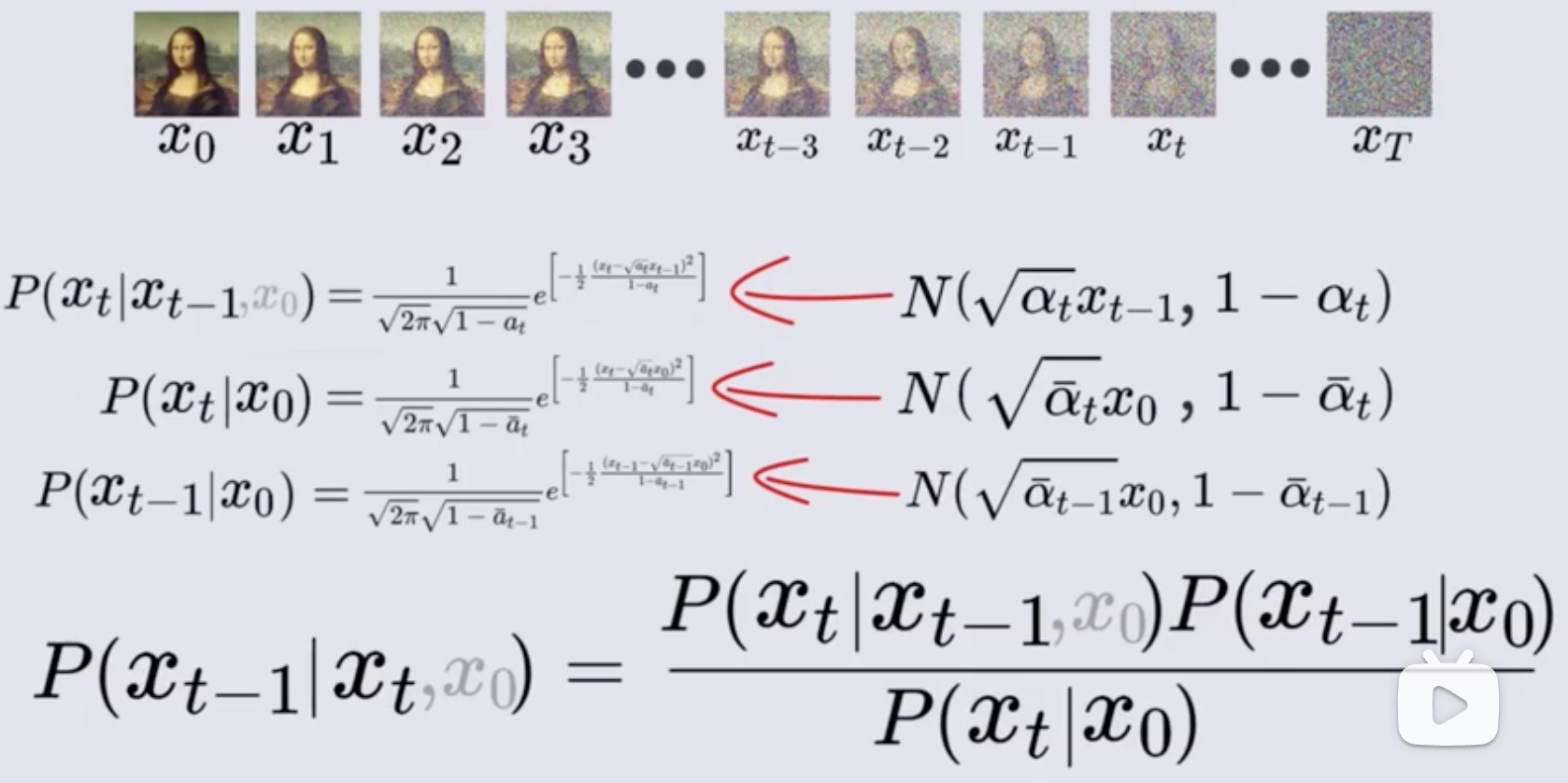
① p ( x t ∣ x t − 1 ) p(x_t|x_{t-1}) p(xt∣xt−1):~ N ( α t x t − 1 , 1 − α t ) N(\sqrt{\alpha_t} x_{t-1}, 1-\alpha_t) N(αtxt−1,1−αt)
注意上上个图中的第一个式子,这里的 ϵ t \epsilon_t ϵt 是服从 (0,1) 分布的高斯噪声,乘以前面的系数 1 − α t \sqrt{1-\alpha_t} 1−αt 后,变成服从 N ( 0 , 1 − α t ) N(0, 1-\alpha_t) N(0,1−αt) 的分布,然后再加上后面的一项 α t × x t − 1 \sqrt{\alpha_t} \times x_{t-1} αt×xt−1 后,均值就变化了,变成了服从 N ( α t x t − 1 , 1 − α t ) N(\sqrt{\alpha_t} x_{t-1}, 1-\alpha_t) N(αtxt−1,1−αt) 的分布,这就是给定 x t − 1 x_{t-1} xt−1 时刻时,对应 x t x_t xt 时刻的概率分布 p ( x t ∣ x t − 1 ) p(x_t|x_{t-1}) p(xt∣xt−1),是一个正态分布
② p ( x t ∣ x 0 ) p(x_t|x_0) p(xt∣x0):~ N ( α ‾ t x 0 , 1 − α ‾ t ) N(\sqrt{\overline{\alpha}_t}\ x_0 ,1-\overline{\alpha}_t) N(αt x0,1−αt)
注意上上个图中的第二个式子,,这里的 ϵ \epsilon ϵ 也是服从 (0,1) 分布的高斯噪声,和前面推法一样,最后就变成了服从 N ( α ‾ t x 0 , 1 − α ‾ t ) N(\sqrt{\overline{\alpha}_t}\ x_0 ,1-\overline{\alpha}_t) N(αt x0,1−αt) 的分布
③ p ( x t − 1 ∣ x 0 ) p(x_{t-1}|x_0) p(xt−1∣x0):~ N ( α ‾ t − 1 x 0 , 1 − α ‾ t − 1 ) N(\sqrt{\overline{\alpha}_{t-1}}\ x_0 ,1-\overline{\alpha}_{t-1}) N(αt−1 x0,1−αt−1)
使用相同的计算方式来计算
得到了上面三个部分的均值和方差后,就能用正态分布的概率密度函数形式来表示
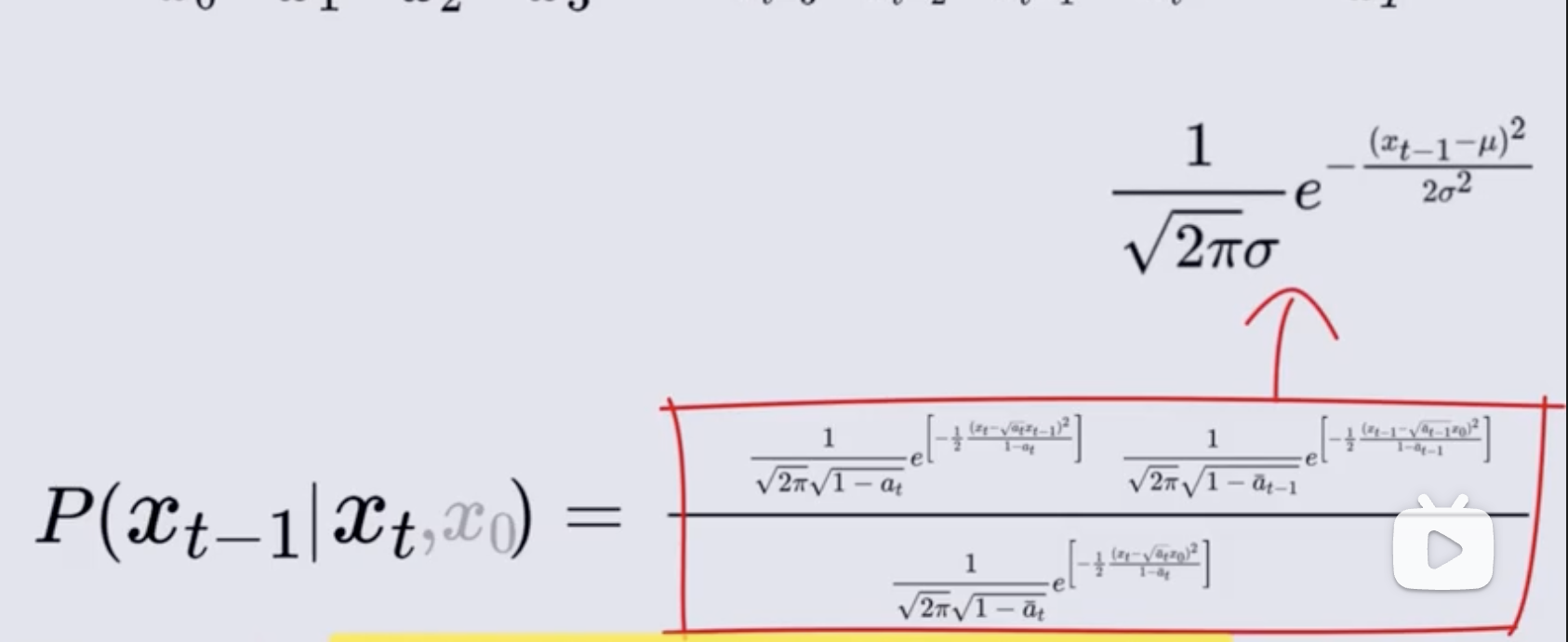
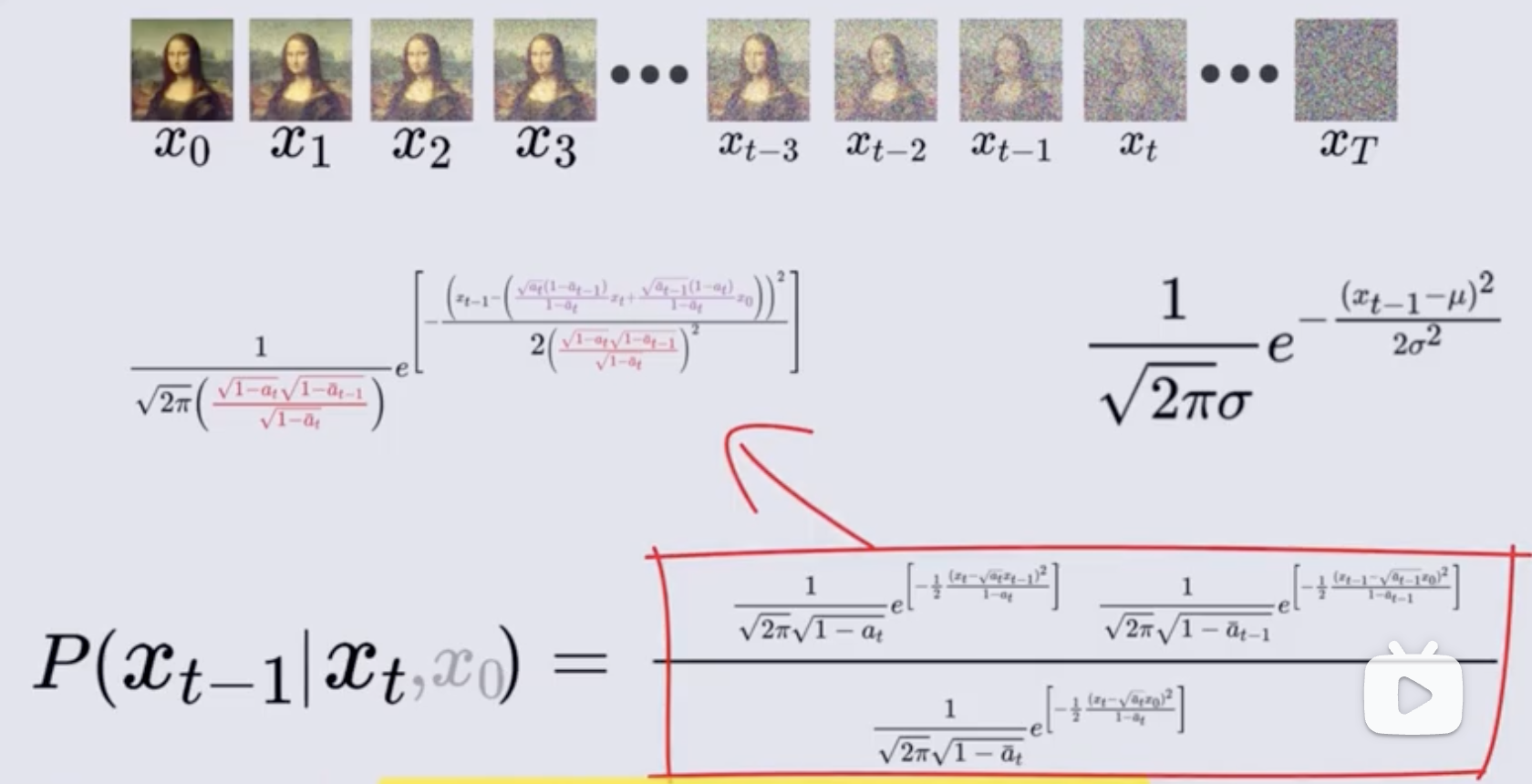
然后再将这些密度函数带入贝叶斯公式中:
目标是求解给定 x t x_t xt 条件下 x t − 1 x_{t-1} xt−1 的概率,实际上也是正态分布,所以就需要将上面的式子变换侧灰姑娘 x t − 1 x_{t-1} xt−1 的概率密度函数形式
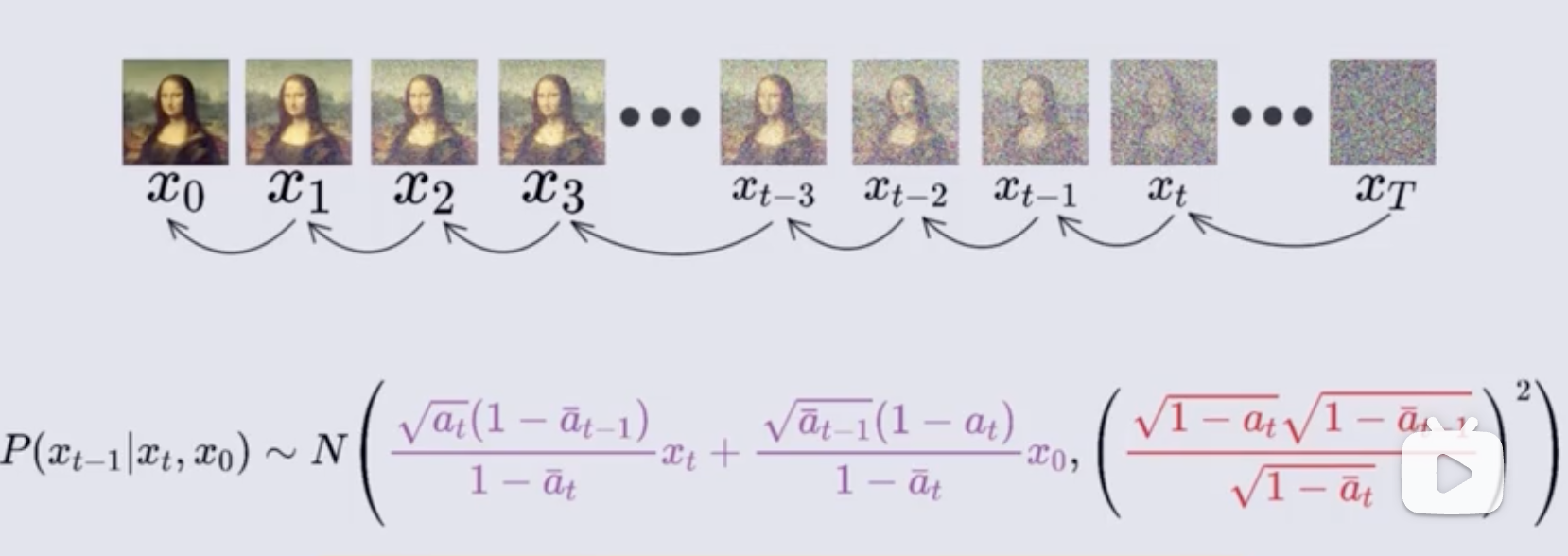
所以,最终给定 x t x_t xt 条件下, x t − 1 x_{t-1} xt−1 的概率分布如下
然后就从 x T x_T xT 时刻,不断使用这个关系,得到 x t x_{t} xt, x t − 1 x_{t-1} xt−1,直到 x 0 x_0 x0 的分布,这里的所有图像都可以看成一个分布
至此,整个推理过程就结束了,所以需要神经网络来做什么呢:
给定一张随机噪声 x T x_T xT,通过神经网络预测噪声 ϵ \epsilon ϵ,然后根据预测到的噪声就能得到前一时刻图像的概率分布,这个概率分布就是上面图中的 p ( x t − 1 ∣ x t , x 0 ) p(x_{t-1}|x_t,x_0) p(xt−1∣xt,x0),然后用此概率分布进行随机采样,就能得到一张前一时刻的图像,然后再将这个前一时刻的图像使用神经网络预测噪声,不断重复这个预测、采样、预测、采样的过程,就能得到 x 0 x_0 x0 了
而且这个最开始的图像 x T x_T xT 其实近似于标准正态分布,所以随机采样即可
从 T 时刻像 0 时刻递减的过程中可以看出,前一时刻的图像的正态分布的标准差越来越小,逐渐接近于 0,其实就是上面图中大红色字那部分表示的标准差,也就是说前一时刻的图像分布越来越靠近均值
2.3 训练和推理
模型的结构:U-Net
模型每次的输入: x t x_t xt 和 time embedding t t t
模型每次的输出:噪声
每次从 t t t 时刻到 t − 1 t-1 t−1 时刻的模型 U-Net 的参数都是共享的
模型学习的目标:
不断的逆向去掉噪声,学习的目标就是让每步逆向预测的噪声 ϵ θ ( x t , t ) \epsilon_{\theta}(x_t, t) ϵθ(xt,t) 和每步前向添加的噪声 ϵ \epsilon ϵ 尽可能的相近,前向添加噪声的时候虽然是一次进行的,但每次添加的噪声其实是都有记录的。
损失函数:
训练的过程:最小化预测的噪声和添加的噪声的差距
- 第一步:输入原图 x 0 x_0 x0
- 第二步:生成随机噪声 ϵ \epsilon ϵ 和时间 t t t
- 第三步:对原图加噪, x t = α ‾ t x 0 + 1 − α ‾ t ϵ x_t=\sqrt{\overline{\alpha}_t}\ x_0 + \sqrt{1-\overline{\alpha}_t} \ \epsilon xt=αt x0+1−αt ϵ,这里 α ‾ t \overline{\alpha}_t αt 表示累乘
- 第四步:将加噪的图像和时间向量 t 输入神经网络模型,预测噪声 ϵ θ \epsilon_{\theta} ϵθ
- 第五步:计算 loss 并更新模型
推理的过程:
- 从 N ( 0 , 1 ) N(0,1) N(0,1) 中随机生成一个噪声
- 循环 T 步逐步去噪,就从噪声恢复得到了原图