2021-11-14 - 悦读

软阈值迭代算法（ISTA）和快速软阈值迭代算法（FISTA）

写在前面
MATLAB仿真程序
参考文献

写在前面

软阈值迭代算法(Iterative Soft Thresholding Algorithm, ISTA)和快速软阈值迭代算法(Fast Iterative Soft Thresholding Algorithm, FISTA)是求解线性逆问题的经典方法，属于梯度类算法。FISTA是 Beck [1] 等人在ISTA的基础上改进得来的。

博客"优化与算法"[2]中对算法原理作了简单分析并给出matlab仿真实验。获取文献[1]或阅读英文有困难的，可以看看该博客，不过最好还是看原文献。

对于一个线性系统：y = Ax + w，A是MN的已知观测矩阵，y是N1的已知观测结果，w是加性噪声，x是要求解的源。该问题可以用最小二乘法(Least squares)求解。然而，在大多数条件下A是病态的。当A病态时，最小二乘法就不适用了。因为，系统微小的扰动都会导致结果差别巨大。ISTA和FISTA是求解病态系统的一种有效方法。

MATLAB仿真程序

博主不是数学专业的，数学功底也较为薄弱。因此，本博客不对ISTA和FISTA的原理作过多的解释，以免误人子弟。在仔细阅读了博客"优化与算法"[2]后，博主发现其给出的仿真程序并不完全符合文献[1] 的理论推导。因此，博主根据自己对文献[1] 的理解，写了两份程序，来和大家讨论。

固定步长的ISTA

% Iterative Soft Thresholding Algorithm(FISTA)
% written by zhwang @2021-11-13
% Reference: Beck, Amir, and Marc Teboulle. "A fast iterative 
% shrinkage-thresholding algorithm for linear inverse problems." 
% SIAM journal on imaging sciences 2.1 (2009): 183-202.
 
% Inputs:
% y         - measurement vector
% A         - measurement matrix
% lambda    - denoiser parameter in the noisy case
% epsilon   - error threshold
% iter_max - maximum number of amp iterations
%
% Outputs:
% x_hat     - the last estimate
% error     - reconstruction error

function [xhat, error] = ISTA(y, A, lambda, epsilon, iter_max)
    if nargin < 5
        iter_max = 5e3;
    elseif nargin < 4
        iter_max = 5e3; epsilon = 1e-4; 
    elseif nargin < 3
        iter_max = 5e3; epsilon = 1e-4; lambda = 5e-4;
    elseif nargin < 2
        iter_max = 5e3; epsilon = 1e-4; lambda = 5e-4;
    end
    
    N = size(A, 2); % col of A
    errortmp = zeros(iter_max,2);
    
    [~, D] = eig(A'*A);
    Lf = 2*max(diag(D)); % A Lipschitz constant of ∇f.
    t = 1/Lf;
    x0 = zeros(N, 1);
    % 开始迭代
    for i = 1:iter_max
        temp = x0 - 2*t*A'*(A*x0-y); 
% A fast iterative shrinkage-thresholding algorithm for linear inverse
% problems 中的方法
        x1 = (abs(temp)-lambda*t) .* sign(temp); % 收敛慢
% A Fixed-Point Continuation Method forl1-Regularized Minimization with 
% Applications to Compressed Sensing  [3] 中的方法
%         x1 = max(abs(temp)-lambda*t, 0) .* sign(temp); % 收敛快
        errortmp(i,1) = norm(x1 - x0) / norm(x1);
        errortmp(i,2) = norm(y - A*x1);
        if errortmp(i,1) < epsilon || errortmp(i,2) < epsilon
            break
        else
            x0 = x1;
        end
    end
    xhat = x1;
    error = errortmp(1:i,:);
end

固定步长的FISTA

% Fast Iterative Soft Thresholding Algorithm(FISTA)
% written by zhwang @2021-11-13
% Reference: Beck, Amir, and Marc Teboulle. "A fast iterative 
% shrinkage-thresholding algorithm for linear inverse problems." 
% SIAM journal on imaging sciences 2.1 (2009): 183-202.
 
% Inputs:
% y         - measurement vector
% A         - measurement matrix
% lambda    - denoiser parameter in the noisy case
% epsilon   - error threshold
% iter_max - maximum number of amp iterations
%
% Outputs:
% x_hat     - the last estimate
% error     - reconstruction error

function [xhat, error] = FISTA(y, A, lambda, epsilon, iter_max)
    if nargin < 5
        iter_max = 5e3;
    elseif nargin < 4
        iter_max = 5e3; epsilon = 1e-4; 
    elseif nargin < 3
        iter_max = 5e3; epsilon = 1e-4; lambda = 5e-4;
    elseif nargin < 2
        iter_max = 5e3; epsilon = 1e-4; lambda = 5e-4;
    end
    
    N = size(A, 2); % col of A
    errortmp = zeros(iter_max,2);
    
    [~, D] = eig(A'*A);
    Lf = 2*max(diag(D)); % A Lipschitz constant of ∇f.
    t = 1/Lf;
    t1 = 1; % 
    x0 = zeros(N, 1);
    y1 = x0;
    % 开始迭代
    for i = 1:iter_max
        temp = y1 - 2*t*A'*(A*y1-y); 
% A fast iterative shrinkage-thresholding algorithm for linear inverse
% problems 中的方法
%         x1 = (abs(temp)-lambda*t) .* sign(temp); % 收敛慢
% A Fixed-Point Continuation Method forl1-Regularized Minimization with 
% Applications to Compressed Sensing [3] 中的方法
        x1 = max(abs(temp)-lambda*t, 0) .* sign(temp); % 收敛快
        t2 = 1/2*(1+sqrt(1+4*t1^2));
        y2 = x1 + (t1 - 1)/t2 * (x1 - x0);
        errortmp(i,1) = norm(y2 - y1) / norm(y2);
        errortmp(i,2) = norm(y - A*y2);
        if errortmp(i,1) < epsilon || errortmp(i,2) < epsilon
            break
        else
            x0 = x1;
            y1 = y2;
            t1 = t2;
        end
    end
    xhat = y2;
    error = errortmp(1:i,:);
end

测试实例

clear all; clc;
N = 441; 
n = 1:N;
M = 289; 
K = 10 ;
x = zeros(N,1);
T = 5*randn(K,1); % 实点
% T = 5 * (randn(K,1) + 1i*randn(K,1)); % 复点
index_k = randperm(N);
x(index_k(1:K)) = T;
 
A = randn(M,N);
y = A * x; %  + e 
y = awgn(y, 10);

[x_rec1,error1] = ISTA(y,A,5e-0,5e-6,5e3) ;
[x_rec2,error2] = FISTA(y,A,5e-2,5e-5,5e3) ;

%%
figure
plot(1:N,abs(x),'b*',1:N,abs(x_rec1),'ro');
legend('target','reconstract');
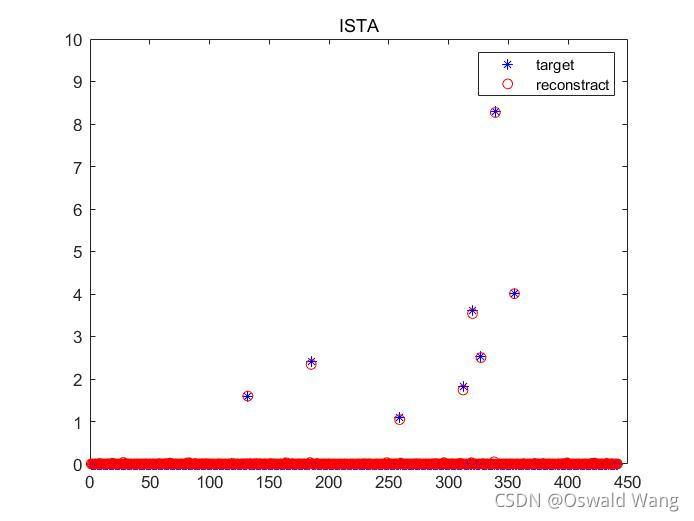
title('ISTA');
figure
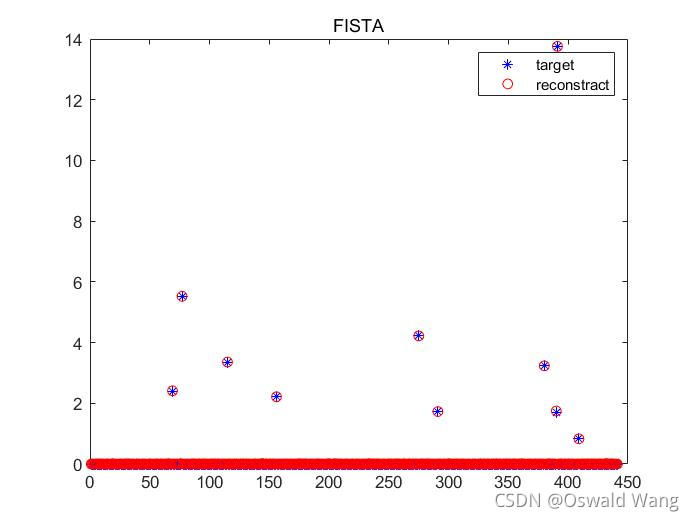
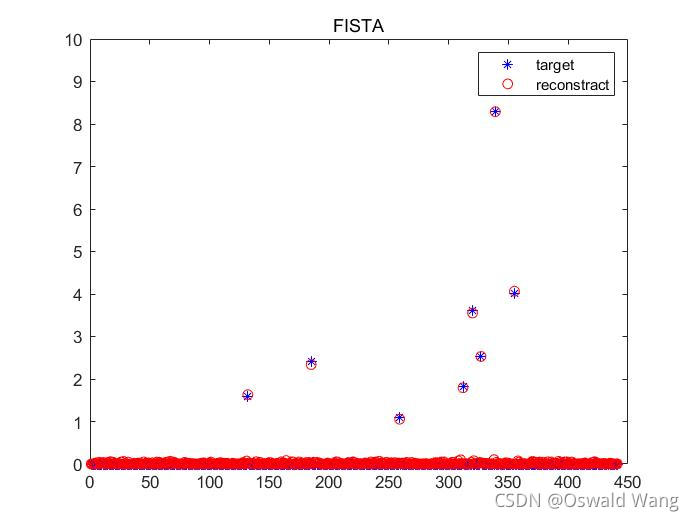
plot(n, abs(x), 'b*', n, abs(x_rec2), 'ro'); legend('target','reconstract');
title('FISTA');

该测试例程与博客"优化与算法"[2]中的主要不同是：本博客中的观测矩阵A是随机生成的，而[2]中的观测矩阵A的列是正交的。

仿真结果

无噪声时
在这里插入图片描述

SNR = 10 dB时

参考文献

[1]: Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM journal on imaging sciences, 2009, 2(1): 183-202.
[2]: https://www.cnblogs.com/louisanu/p/12045861.html
[3]: Hale E T, Yin W, Zhang Y. A fixed-point continuation method for L_1-regularization with application to compressed sensing[R]. 2007.