力扣面试经典150题刷题Day 3 数组和字符串（3）

数组的算法题大多都和dp以及回溯相关，所以今天把最后几道纯数组的题目小结一下

T169 多数元素

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

解题思路

多数元素实际上就是有限制的“众数”，在众数基础上进一步要求众数的数目要占所有元素数目的一半以上，针对此问题主要有四种方法：

1.暴力法，遍历所有元素，设置一个计数器，若计数器值＞n/2，则说明该元素就是多数元素

2.排序法，由于题目说明必定有一个多数元素，因此只需要将元素按递增排序，第⌊ n/2 ⌋+1个个元素（下标为⌊ n/2 ⌋）必定为多数元素

3.摩尔投票法，这个方法还没见过，重点关注下

4.哈希法，使用哈希映射（HashMap）来存储每个元素以及出现的次数。对于哈希映射中的每个键值对，键表示一个元素，值表示该元素出现的次数。

方法一：暴力法

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        for(int i=0;i<nums.size();i++){
            int value=nums[i];
            int count=0;
            for(int j=0;j<nums.size();j++){
                if(nums[j]==value) count++;  
            }
            if(count>nums.size()/2) return value;
        }
        return 0;
    }
};

时间复杂度：O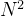（ $N^{2}$ ）

空间复杂度：O（1）

方法二：排序法

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        return nums[nums.size()/2];
    }
};

没啥难度，都有现成的库函数，但是有可能面试或者笔试的时候不让用sort，排序算法比较好用的就是快排，由于复试不上机只需要手撕代码，因此下面我放个伪码

partition是用于划分的函数，408的代码题以及很多复试和面试里面经常会涉及到快排，

int partition(int nums[],int left,int right){
        int mid=left;
        while(left<right){
            while(nums[right]>=nums[mid] && right>left) right--;  
            //有指针指向元素大于mid
            nums[left]=nums[right];
            while(nums[left]<=nums[mid] && right>left) left++;   
            //左指针元素指向元素小于mid
            nums[right]=nums[left];
        } 
        nums[left]=nums[mid];   //枢轴元素
        return left;            //返回枢轴元素的下标
    }


void QuickSort(int nums[],int begin,int end){
        int n=nums.size()-1;
        int m=partition(nums,0,n);   //枢轴元素
        QuickSort(nums,0,m-1);       //对枢轴元素左边元素进行快排
        QuickSort(nums,m+1,n);       //对枢轴元素右边元素进行快排
    }

时间复杂度：O（nlogn），无论是sort还是快排都是一样的

空间复杂度：O（1）

方法三：摩尔投票法

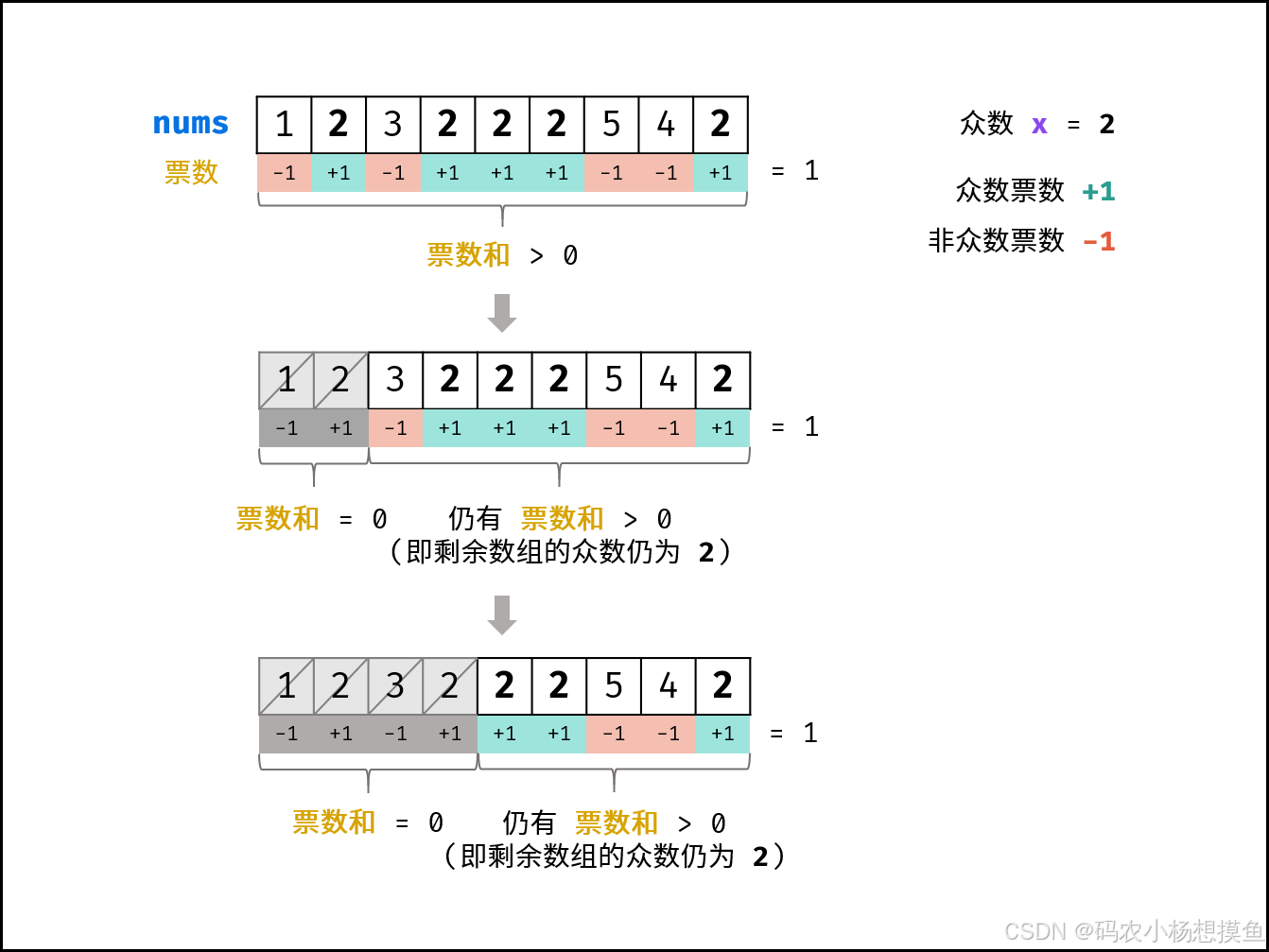
1.重要推论

假设多数元素个数为x，数组长度为n。

推论一：若记众数的票数为 +1 ，非众数的票数为 −1 ，则一定有所有数字的票数和 >0 。

推论二：若数组的前 a 个数字的票数和 =0 ，则数组剩余 (n−a) 个数字的票数和一定仍 >0 ，即后 (n−a) 个数字的众数仍为 x 。

注：此处众数就是多数元素，和数学领域上的众数不同

数组的首元素为n0，初始时假设x=n0，计时器值count=1；

情况一：假设n0就是我们要找的多数元素的话，通过上述方法，最后剩下的元素一定为多数元素

情况二：假设n0不是多数元素，假设在下一次count=0时遍历了m个元素，在这m个元素中至少有0个多数元素x，至多有m/2个多数元素x；因此，根据推论二，在接下来的n-m个元素中的多数元素依旧是x，根据此性质可以不断缩小区间范围，将情形二转化为情形一为止

原文链接169. 多数元素 - 力扣（LeetCode），原贴博主其实讲的非常透彻了

2.算法实现

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int candidate=0;
        int vote=0;
        int n=nums.size();
        for(int i=0;i<n;i++){   
            if(vote==0) candidate=nums[i];  
            //先判断是因为指针永远指向遍历元素的后一个位置
            vote+=(candidate==nums[i])?1:-1;     
        }
        //验证candidate是否为多数元素，题目没要求的话需要另外判断一下
        int count=0;
        for(int num:nums){
            if(num==candidate) count++; 
        }
        return (count>n/2)?candidate:1e9;  
        //返回1e9表示无多数元素
    }
};

时间复杂度：O（N）

空间复杂度：O（1）

方法四：哈希表法

哈希是数据结构的一种，以键值对的形式存储数据。

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int n=nums.size();
        map<int,int> data;
        for(int num:nums){
            data[num]++;
            if(data[num]>n/2) return num;
        }
        return -1;  //不存在
    }
};

时间复杂度：O（N)

空间复杂度：O（N），因为至多有N/2个键值对（n/2+1个多数元素，其余每个元素两两各不相同)

T189 轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数

示例 1 输入: nums = [1,2,3,4,5,6,7], k = 3 输出: [5,6,7,1,2,3,4]
示例 2 输入：nums = [-1,-100,3,99], k = 2 输出：[3,99,-1,-100]

这题做王道408代码题的时候遇到过，好像也是真题来着，反正这题是会背了，这里就写两种办法吧。

方法一：使用额外数组

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> newArr(n);
        for (int i = 0; i < n; ++i) {
            newArr[(i + k) % n] = nums[i];
        }
        nums.assign(newArr.begin(), newArr.end());
    }
};

唯一需要注意的就是k可能会大于n，需要取余，k mod n

时间复杂度：O（n)

空间复杂度：O（n）

方法二：原地轮转

说实话，没提前做过我肯定也想不到，直接记住吧，当套路了，一堆理论看了半天云里雾里的，可能是功力不够。而且最开始还没注意到k可能比n大的条件，测试出错才发现这个问题。

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int len=nums.size();
        int move=k%len;     //还需要考虑k>len时的情况，且右移len个实际上相当于没有移动
        reserve(nums,0,len-move-1);
        reserve(nums,len-move,len-1);
        reserve(nums,0,len-1);
    }

    //逆置数组元素
    void reserve(vector<int>& nums,int start,int end){
        while(end>start){
            int temp;
            temp=nums[start];
            nums[start]=nums[end];
            nums[end]=temp;
            start++;
            end--;
        }
    }
};

时间复杂度：O（N）

空间复杂度：O（1）

T238 除自身以外数组的乘积

给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

解题思路

其实刚开始就想用除法，但是不能用，如果可用的话需要判断0元素这个特殊情况

既然不能使用除法的话，又要求在O（N）的时间复杂度内完成，因此必定数据量较大

其实最开始没有太多思路，看了提示才知道两个东西：前缀乘积和后缀乘积

前缀乘积是指下标为i的元素之前0~（i-1）范围内元素的乘积

后缀乘积是指下标为i的元素之前（i+1）~n范围内元素的乘积

代码实现

最开始的代码写成这样，毫无意外地超时了

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n=nums.size();
        vector<int> front(n,0);   //前缀乘积
        vector<int> rear(n,0);    //后缀乘积
        for(int i=0;i<n;i++){
            if(i==0){
                front[0]=1;
                rear[0]=multiple(nums,1,n-1);
            }
            else if(i==n-1){
                rear[i]=1;
                front[i]=multiple(nums,0,n-2);
            }
            else{
                front[i]=multiple(nums,0,i-1);
                rear[i]=multiple(nums,i+1,n-1);
            }
        }
        vector<int> answer(n,0);
        for(int i=0;i<n;i++){
            answer[i]=front[i]*rear[i];
        }
        return answer;
    }

    //计算数组下表start开始到end结束的数组中所有元素的乘积
    int multiple(vector<int>& nums,int start,int end){
        int result=1;
        for(int i=start;i<end+1;i++){
            result=result*nums[i];
        }
        return result;
    }
};

时间复杂度:O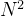（ $N^{2}$ ）

空间复杂度:O(1)

后来才发现题目要求n级别的时间复杂度，因此想到了用空间换时间的思路，不用直接乘。

开辟两个数组，分别用于存储所有元素的前缀乘积和后缀乘积。初始化nums【0】前缀乘积为1，因此某个元素的前缀乘积=（前一个元素值）*（前一个元素的前缀乘积）。后缀乘积同理，初始化nums【n-1】后缀乘积为1，某元素后缀乘积=（后一个元素值）*（后一个元素的后缀乘积）

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n=nums.size();
        vector<int> front(n,0);   //前缀乘积
        vector<int> rear(n,0);    //后缀乘积
        for(int i=0;i<n;i++){
            if(i==0) front[0]=1;
            else front[i]=front[i-1]*nums[i-1];
        }
        for(int i=n-1;i>=0;i--){
            if(i==n-1) rear[n-1]=1;
            else rear[i]=rear[i+1]*nums[i+1];
        }
        vector<int> answer(n,0);
        for(int i=0;i<n;i++){
            answer[i]=front[i]*rear[i];
        }
        return answer;
    }
};

时间复杂度：O（N）

空间复杂度：O（N）