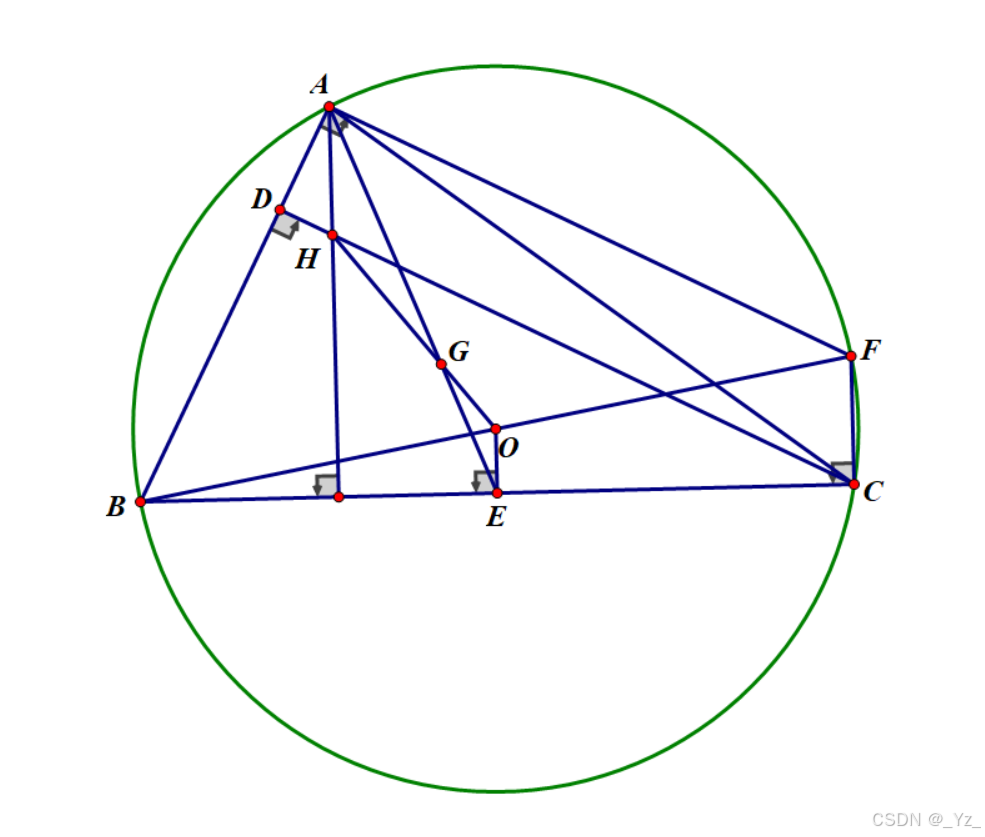
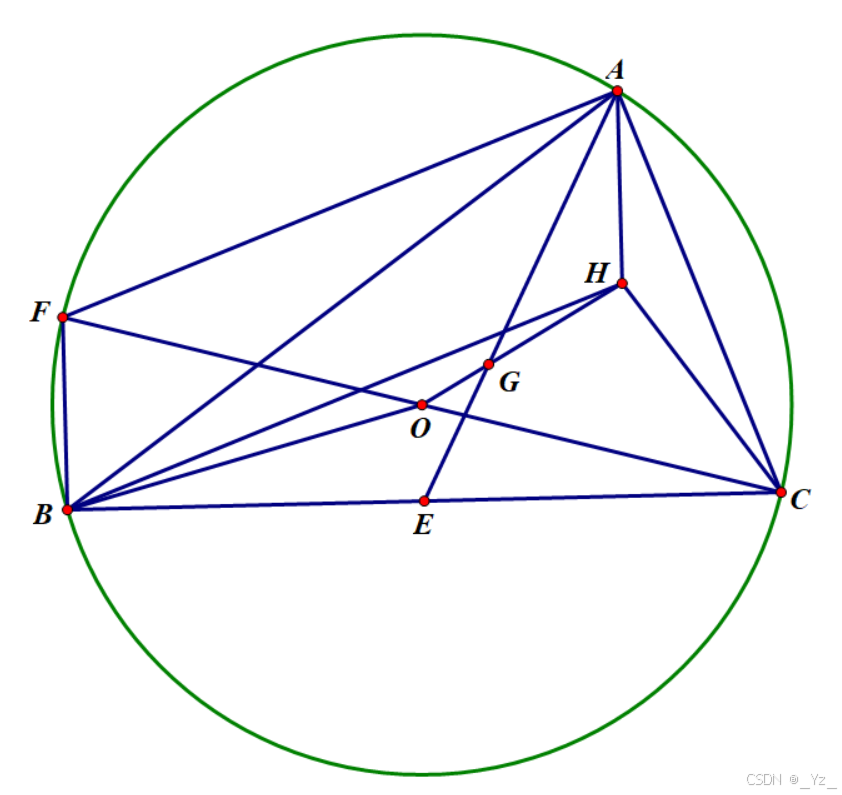
欧拉线是指:三角形的外心、重心和垂心,依次位于同一直线上,这条直线就叫三角形的欧拉线。
那么如何证明呢?
以下有两种方法证明:
-
几何法
证明思路如下:若要证明 H , G , O H,G,O H,G,O 共线,则要证明 ∠ A G H = ∠ E G O \angle AGH = \angle EGO ∠AGH=∠EGO
由于 A H ⊥ B C AH\perp BC AH⊥BC, B F BF BF 为 ⊙ O \odot O ⊙O 直径, F C ⊥ B C FC\perp BC FC⊥BC, O E OE OE 为弦 B C BC BC 中线,根据垂径定理可得 O E ⊥ B C OE\perp BC OE⊥BC
所以, O E / / F C / / A H , ∠ H A G = ∠ O E G OE // FC // AH,\angle HAG = \angle OEG OE//FC//AH,∠HAG=∠OEG
又 ∵ ∠ B A F = ∠ B D C = 9 0 ∘ \because \angle BAF = \angle BDC = 90^{\circ} ∵∠BAF=∠BDC=90∘
∴ A F / / H C \therefore AF // HC ∴AF//HC
综上,可得四边形 A H C F AHCF AHCF 为平行四边形。
所以 A H = F C = 2 O E , A H E O = 2 AH = FC = 2OE,\frac{AH}{EO}=2 AH=FC=2OE,EOAH=2
根据三角形重心的性质,可得 A G E G = 2 \frac{AG}{EG}=2 EGAG=2
因此,易得 △ A G H ∼ △ E G O , ∠ A G H = ∠ E G O \triangle AGH \sim \triangle EGO,\angle AGH = \angle EGO △AGH∼△EGO,∠AGH=∠EGO,即 H , G , O H,G,O H,G,O 三点共线。
同时我们也得到 H G = 2 E G HG = 2EG HG=2EG(即外心到重心的距离等于垂心到重心距离的一半)
-
向量法
证明思路如下:由图易得,四边形 A H B F AHBF AHBF 为平行四边形。
∴ O H → = O B → + B H → = O B → + F A → = O B → + F O → + O A → = O A → + O B → + O C → \therefore \overrightarrow{OH} = \overrightarrow{OB} + \overrightarrow{BH} = \overrightarrow{OB} + \overrightarrow{FA} = \overrightarrow{OB} + \overrightarrow{FO} + \overrightarrow{OA} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} ∴OH=OB+BH=OB+FA=OB+FO+OA=OA+OB+OC
又 ∵ O G → = O A → + A G → = O A → + 2 3 A E → = O A → + 2 3 ( A B → + B E → ) = O A → + 2 3 ( A O → + O B → + 1 2 B C → ) = O A → + 2 3 ( A O → + O B → + 1 2 B O → + 1 2 O C → ) = O A → + 2 3 ( − O A → + 1 2 O B → + 1 2 O C → ) = 1 3 ( O A → + O B → + O C → ) \because \overrightarrow{OG} = \overrightarrow{OA} + \overrightarrow{AG} = \overrightarrow{OA} + \frac{2}{3}\overrightarrow{AE} = \overrightarrow{OA} + \frac{2}{3}\left(\overrightarrow{AB} + \overrightarrow{BE}\right) = \overrightarrow{OA} + \frac{2}{3}\left(\overrightarrow{AO} + \overrightarrow{OB} + \frac{1}{2}\overrightarrow{BC}\right) = \overrightarrow{OA} + \frac{2}{3}\left(\overrightarrow{AO} + \overrightarrow{OB} + \frac{1}{2}\overrightarrow{BO} + \frac{1}{2}\overrightarrow{OC}\right) = \overrightarrow{OA} + \frac{2}{3}\left(-\overrightarrow{OA} + \frac{1}{2}\overrightarrow{OB} + \frac{1}{2}\overrightarrow{OC}\right) = \frac{1}{3}\left(\overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC}\right) ∵OG=OA+AG=OA+32AE=OA+32(AB+BE)=OA+32(AO+OB+21BC)=OA+32(AO+OB+21BO+21OC)=OA+32(−OA+21OB+21OC)=31(OA+OB+OC)
∴ O H → = 3 O G → , O G → = 1 2 G H → \therefore \overrightarrow{OH} = 3\overrightarrow{OG},\overrightarrow{OG} = \frac{1}{2}\overrightarrow{GH} ∴OH=3OG,OG=21GH
∴ O , H , G \therefore O,H,G ∴O,H,G 三点共线