本文的目的是从B树的起源讲起,再到java语言完整的实现,以达到对B树有一个全面的认识,如果你打算学习并实现B树(但是能在有生之年去实现一遍B树的人很少),那么看完本文就应该可以了。如果你想找B树的应用,那本文不适合。
B树的起源
我一直坚信,一个东西或一项技术的出现一定是有原因的,如果我们能找到那个原因,就能像创造者一样思考为什么要这样,为什么那个人不是我?下面开始。
在1970年,Bayer&McCreight发表的论文《ORGANIZATION AND MAINTENANCE OF LARGE ORDERED INDICES 》(大型有序索引的组织和维护)中提出了一种新的数据结构来维护大型索引,这种数据结构在论文中称为B-Tree,看论文的摘要:
ABSTRACT
Organization and maintenance of an index for a dynamic random access file is considered. It is assumed that the index must be kept on some pseudo random access backup store like a disc or a drum. The index organization described allows retrieval, insertion, and deletion of keys in time proportional to l o g k I log_kI logkI where I is the size of the index and k is a device dependent natural number such that the performance of the scheme becomes near optimal. Storage utilization is at least 50% but generally much higher. The pages of the index are organized in a special data-structure, so-called B-trees. The scheme is analyzed~ performance bounds are obtained, and a near optimal k is computed. Experiments have been performed with indices up to i00,000 keys. An index of size 15,000 (i00,000) can be maintained with an average of 9 (at least 4) transactions per second on an IBM 360/44 with a 2311 disc.
翻译过来:
考虑组织和维护动态随机访问文件的索引, 假设索引必须保存在某些伪随机访问备份存储中,如光盘或鼓。 所描述的索引组织必须在
l
o
g
k
I
log_kI
logkI时间内成比例地检索,插入和删除键,其中
I
I
I是索引的大小,
k
k
k是依赖于设备的自然数,使得方案的性能变得接近最优。 存储利用率至少为50%,但通常要高得多。 索引的页面组织在一个特殊的数据结构中,即所谓的B树。 分析该方案〜获得性能界限,并计算近似最优k。 已经使用高达100,000个键的索引进行了实验。 在具有2311个光盘的IBM 360/44上,可以维持大小为15,000(i00,000)的索引,平均每秒9次(至少4次)事务。
B树的定义1
还是先看看B树在论文中如何定义的:
h
h
h:代表树的高度,
k
k
k是个自然数,一个B树要么是空的,要么满足以下条件:
1.所有叶子节点到根节点的路径长度相同,即具有相同的高度;
2.每个非叶子和根节点(即内部节点)至少有 k + 1 k+1 k+1个孩子节点,根至少有2个孩子;
3.每个节点最多有 2 k + 1 2k+1 2k+1个孩子节点。
4.每个节点内的键都是递增的(后文提到)
看完了这几个定义,你肯定会问:
k
k
k是什么? 好吧,论文在插入一节提到了:
意思就是:这个B树的每个节点实际上代表了一页(Page),这一页可以看成是一个磁盘块的大小,比如1024,那么就可以存储1024个键,那么这个k就等于512,因为一页最大为2k,最小为k个键,k看来可以是自己定义的,根据你的存储硬件来决定。下图是论文中的一页,可看成是个数组:
B树定义2
但是,大家在网上搜索时会发现定义并不唯一,普遍采用了m阶(代表order,中文翻译为阶)来定义:
- 每个节点最多有m个孩子。
- 每个内部节点(除去叶节点和根节点)至少有⌈m/2⌉(向上取整)孩子。
- 如果根不是叶节点,则根至少有两个孩子。
- 所有叶子都出现在同一层。
- 具有k个孩子的非叶节点包含k-1个键,当然节点内的键也是递增的。
这个版本是Knuth’s 提出的,可以在下面的期刊中找到: The Art Of Computer Programming 第494页,定义为如下:
定义比较
在网上可能会有这样的比较:一个是按度(degree,树的度为最大节点的度,节点的度就是节点的孩子数),也就是上面的定义1,一个是按阶(order),也就是定义2。
其实,稍微对比一下就会发现,这两个定义是同一个东西,他们的关系就是 2 k + 1 = m 2k+1=m 2k+1=m(因为 ⌈ m / 2 ⌉ 到 m ⌈m/2⌉ 到 m ⌈m/2⌉到m对应着 k + 1 到 2 k + 1 k+1 到 2k+1 k+1到2k+1,开始定义很明确,所以如果非要比,那么 m m m一般是奇数) .当然,也不用纠结,看看下文为啥会有这些改变。
还有个关键点:即便是每个节点没有存满,也需要分配固定大小的容量,所以才有了存储利用率大于50%一说。
这样的话,定义就基本明白了。
为何术语不统一
为什么关于B树的术语在文献上并不统一(内容来自wiki)。
Order如何定义
Bayer&McCreight(1972),Comer(1979)(参考论文:https://dl.acm.org/citation.cfm?doid=356770.356776 )和其他人将B树的Order定义为非根节点中的最小键数。 Folk&Zoellick(1992)指出此术语含糊不清,因为最大键数不明确。Order为3的 B树可能最多包含6个键或最多7个键。 Knuth(1998)通过将Order定义为最大子项数(比最大键数多一个)来避免此问题,也就是我们现在普遍使用的。
叶子(Leaf)如何定义
叶子一词也不一致。 Bayer&McCreight(1972)认为叶子层是最底层的键,但Knuth认为叶子层低于最底层的键,没有孩子也没有指针(Folk&Zoellick 1992)。
实现的多样性
所以B树有许多种实现。在某些设计中,叶子可能包含整个数据记录; 在其他设计中,叶子可能只保存指向数据记录的指针。但这些并不是B树的基础概念。
为简单起见,大多数作者假设有一定数量的键适合节点。基本假设是键大小是固定的,节点大小是固定的。在实践中,可以使用可变长度的键(Folk&Zoellick 1992)。
理解与实现
关于阶定义的实现
关于普遍存在的一种按照阶的不完全的实现方式: https://algs4.cs.princeton.edu/code/edu/princeton/cs/algs4/BTree.java.html
这个算法需要注意2点:
- 上面代码里的m必须是偶数的,为什么,可以查看:stackoverflow,回答是这并不绝对,只是考虑到性能方面的影响,所以,我进行了一点点修改,让它可以传入奇数的m,具体代码查看:B树实现代码片
- 这颗B树实现简单,但是只能在叶子节点上存储数据,也就是说非叶节点只有key,没有value。
但是这不是本文要讲的方式,本文按照度的定义来讲, t t t代表一个自定义的整数( t > = 2 t>=2 t>=2)表示树的最小度数,一个节点(除根外)的key的范围为( k − 1 到 2 k − 1 k-1 到 2k-1 k−1到2k−1),下面具体看。
本文遵从的定义
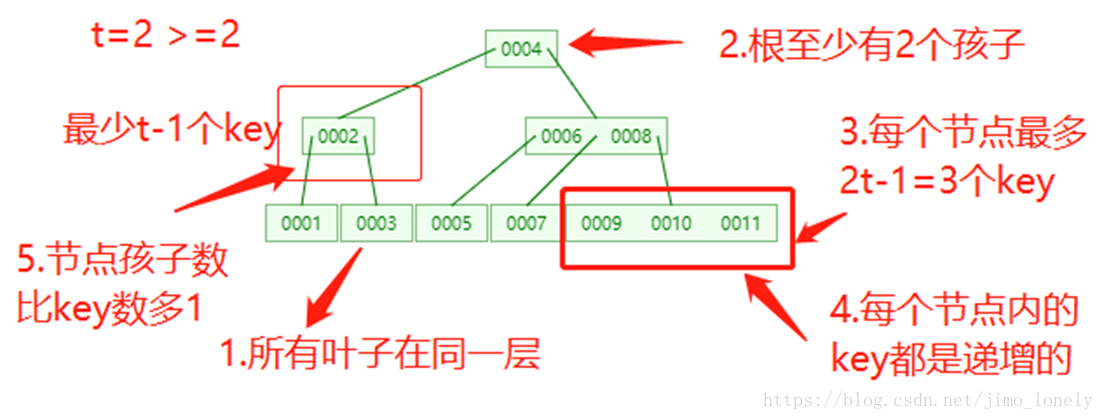
我们按照《算法导论》第3版第18章中的B树定义来实现:
- 所有叶子节点到根节点的路径长度相同,即具有相同的高度;
- 每个非叶子和非根节点(即内部节点)至少有t-1个孩子节点;根至少2个孩子
- 每个节点最多有2t个孩子节点。
- 每个节点内的键都是递增的
- 每个节点的孩子比key的个数多1
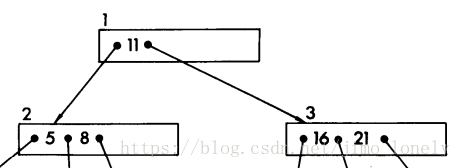
这次用 t t t 来表示B树的最小度数(任意节点最少有 t t t 个孩子),看下图就明白了:
这样树的节点构成如下:
/**
* B树中的节点。
*/
private static class BTreeNode<K, V> {
/**
* 节点的项,按键非降序存放
*/
private List<Entry<K, V>> entries;
/**
* 内节点的子节点
*/
private List<BTreeNode<K, V>> children;
/**
* 是否为叶子节点
*/
private boolean leaf;
/**
* 键的比较函数对象
*/
private Comparator<K> kComparator;
private BTreeNode() {
entries = new ArrayList<>();
children = new ArrayList<>();
leaf = false;
}
...
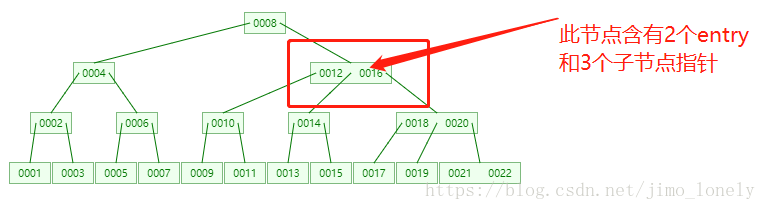
其中每个节点包括键值对的Entry和指向子节点的children指针列表,他们的长度差一,如下图:
而每个节点里的一个Entry就是存放key和value的键值对:
private static class Entry<K, V> {
private K key;
private V value;
public Entry(K k, V v) {
this.key = k;
this.value = v;
}
// getter/setter
@Override
public String toString() {
return key + ":" + value;
}
}
查询
和排序二叉树的搜索很类似,只是换成多叉和多项。
输入key,记住每个节点的key都是有序的
- 从根节点开始找,如果根节点里有,则返回;否则找到对应的下标去子节点递归搜索;
- 如果到了叶子节点还没找到,那就找不到。
下面是部分代码,帮助理解,详细请在后面看完整代码:
public V search(K key) {
return search(root, key);
}
private V search(BTreeNode<K, V> node, K key) {
// 在一个节点内搜索
SearchResult<V> result = node.searchKey(key);
if (result.isExist()) {
return result.getValue();
} else {
if (node.isLeaf()) {
return null;
} else {
// 进入递归
search(node.childAt(result.getIndex()), key);
}
}
return null;
}
插入
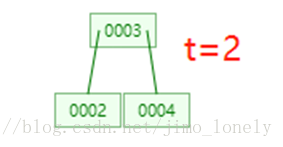
插入稍微复杂一点,涉及到节点满了之后的拆分,也是递归进行的。设我们的
t
=
2
t=2
t=2, 则一个节点最多3个key,至少1个key,至多4个孩子。
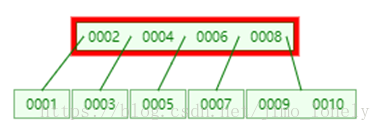
从1-10进行示例:
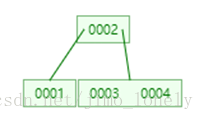
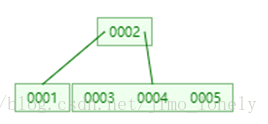
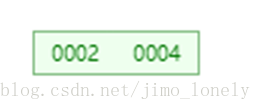
先插入1,3,2,形成根节点
再插入4,在插入4之前就判断出此时已经超过最大容量3,需要分割
根据具体实现,我们先分割,再插入,分割会先提出了
t
−
1
=
1
t-1=1
t−1=1项也就是3作为新的父节点,再把4插进去,这是个递归的过程,因为4比3大,所以是插入到3的右子树里。
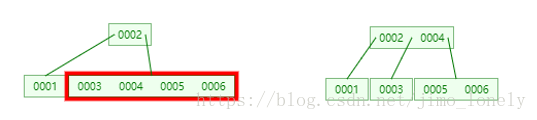
继续插入5
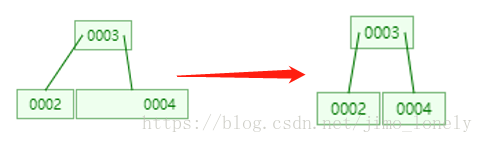
然后是6,发现已经满了,于是分割出4,上升与父节点合并
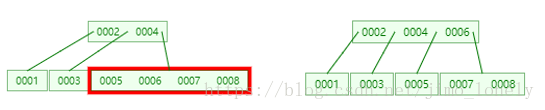
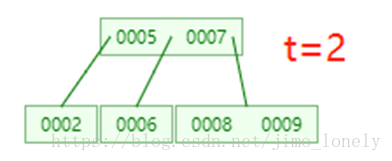
接着7和8,到8的时候依然先分割,于是我们发现根节点已经满了
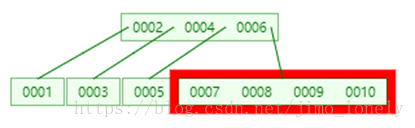
我们接着插入9和10,插入10时,7,8,9节点先分割,于是8会上升
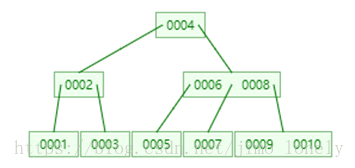
但是这时候根节点已满,所以继续递归的拆分,提出4
最终结果如下
关于代码的实现,大家看看源码就明白了。
删除
删除比较麻烦,但是不复杂,只是分的情况比较多,可以分为以下3种:
- 要删除的key在叶子节点
- 要删除的key在当前节点,但不是叶子
- 要删除的key不在当前节点,可能在子节点中
所以按这3种情况,下面分别讨论。
删除1
要删除的key在叶子节点,直接删除就好:
删除8后
删除2
要删除的key在当前节点,但不是叶子,这可以继续分为2种情况
删除2.1
当前节点左或右子节点key数>=t,如下:
我们删除45,从根节点出发,发现45就在根节点,并且它的左右孩子的key数都大于
t
=
2
t=2
t=2,于是我们用左孩子的最后一个key 43替换45,然后递归删除左孩子的43.
如果左孩子的key数<t,那就用右孩子的第一个去替换,然后递归删除右孩子的第一个key。
删除2.2
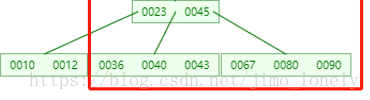
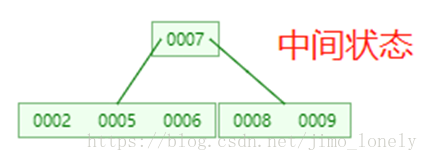
当前节点的左右孩子都只有t-1个key,小于t 。比如下面,我们要删除5,发现5的左右孩子都只有一个key
这时候就可以合并了,合并规则是左孩子的key+要删除的key+右孩子的key,然后合并到左孩子,合并的中间状态如下:(为啥可以合并?因为合并后的key数刚好为
2
t
−
1
2t-1
2t−1)
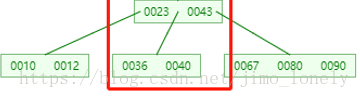
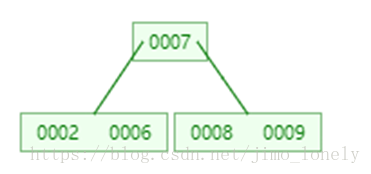
然后递归删除左孩子的5,结果如下:
删除3
要删除的key不在当前节点,可能在子节点中. 这依然分2种情况。
删除3.1
当前节点的一个相邻兄弟的key数>=t,如下,右孩子的key数>=2
我们要删除1,于是进行一次左旋(假如是左孩子的key数>=t,则进行右旋),然后递归删除左节点的1(旋转后还没有删除1,下面的图是最终结果)
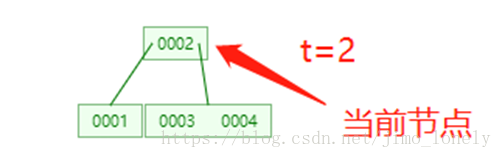
删除3.2
当前节点的所有相邻兄弟的key数都=t-1,如下,当前在3
于是我们进行合并,类似前面2.2的合并:
再递归的删除3(注意,本例很简单,但很可能2和4节点还有子节点,所以要递归进行,不只是为了删除,也可能是调整结构)
删除如何调整结构
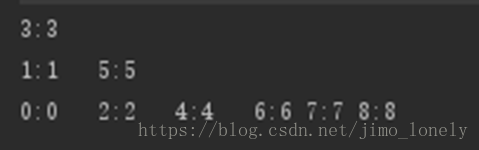
删除还有可能调整结构,即便什么都没删除,下面是一个例子:这是个打印出来的B树
如果我们删除9,9并不存在,但会得到以下结果:
为什么?仔细一分析就知道第一步时就满足删除3.2的情况了,所以进行了合并,这个例子在我源码的测试代码里。
另外,这只是根据实现的不同而不同,不一定都会改变原树。
复杂度分析
简单的分析一下复杂度把。需要先明白一个概念:
B树为访问外存而生,而什么时候访问呢?就在每次访问节点的时候会查一次磁盘IO,节点内的查询是在内存种进行的,而在访问子节点时就需要访问外存,而最多访问h(树的高度)次节点,因为每一层只会访问一个节点。所以,时间都花在访问节点上。
- n 个 k e y n个key n个key,高度为 h h h的树, t > = 2 t>=2 t>=2,满足 h < = l o g t ( n + 1 ) / 2 h<=log_t(n+1)/2 h<=logt(n+1)/2
- 查询,插入,删除复杂度: O ( t h ) = O ( t l o g t n ) O(th)=O(tlog_tn) O(th)=O(tlogtn)
解释: O ( h ) = O ( l o g t n ) O(h)=O(log_tn) O(h)=O(logtn)次访问外存操作,因为每个节点的 k e y < 2 t key < 2t key<2t 个,所以每个节点的时间为: O ( t ) O(t) O(t), 每一层只访问一个节点,所以总共最多访问 h h h次节点 ,所以复杂度为 O ( t l o g t n ) O(tlog_tn) O(tlogtn)
完成代码
https://code.csdn.net/snippets/2608045
总结
关于B的含义
这个不是重点,但这个B树直接就出现在论文中了,作者也没做说明,所以只能猜测:
- Rudolf Bayer 和 Ed McCreight 于1972年,在Boeing Research Labs 工作时发明了B 树
- Balanced(平衡的), broad(宽的) 或 bushy(浓密的)
- Bayer:他的名字