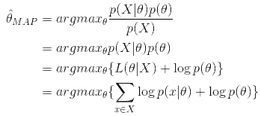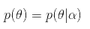1.后验概率是一个条件概率,后验概率可以根据通过贝叶斯公式,用先验概率和似然函数计算出来。
2.极大后验假设
机器学习的任务:在给定训练数据D时,确定假设空间H中的最佳假设。
学习器在候选假设集合H中寻找给定数据D时可能性最大的假设h,h被称为极大后验假设(MAP)确定MAP的方法是用贝叶斯公式计算每个候选假设的后验概率,计算式如下:
h_map=argmax P(h|D)=argmax (P(D|h)*P(h))/P(D)=argmax P(D|h)*p(h) (h属于集合H)
最后一步,去掉了P(D),因为它是不依赖于h的常量。
可进一步表示为:
在实际应用中,先验称为log p(θ),这个先验可以用来描述人们已经知道或者接受的普遍规律。例如在扔硬币的试验中,每次抛出正面发生的概率应该服从一个概率分布,这个概率在0.5处取得最大值,这个分布就是先验分布。先验分布的参数我们称为超参数(hyperparameter)即
我们真正关心的,却是 P(model|observation) 的函数形式,也就是给定了当前的observation (observation是实际观测到的,是确定下来的),到底不同的model的概率是什么。我们想知道不同model 是如何影响 P(model|observation)的。
现在根据贝耶斯原理,
P(model|observation) = [ P(observation|model) * P(model) ]/ P(observation)
其中P(observation) 不太重要,因为我们想知道不同model 是如何影响 P(model|observation)的,或者是贪心的求P(model|observation)的最大值。而P(observation)已经固定下来了,不随model改变,所以我们无视他。
我们如果知道 P(model)(所谓的Prior) 的函数形式,那么就没有什么问题了。此时的P(model|observation)是一个关于model 的函数。报告这个P(model|observation)作为model的函数的函数形式,就叫贝耶斯估计。可是,这需要我们知道P(model)。实际中我们不知道这个玩意,所以一般我们猜一个。
我们如果承认不知道P(model),认为我们对他是无知的话,那么P(model) = 常数 for all model,此时求P(model|observation) 最大值,也就等价于求P(observation|model) 的最大值,这就叫做MLE。
通俗的理解:最大似然估计,就是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
P(黑=8)=p^8*(1-p)^2,现在我想要得出p是多少啊,很简单,使得P(黑=8)最大的p就是我要求的结果,接下来求导的的过程就是求极值的过程啦。
3.极大似然假设
在某些情况下,可假定H中每个假设有相同的先验概率,这样式子可以进一步简化,只需考虑P(D|h)来寻找极大可能假设,也就是说此时是要求似然函数最大。
h_ml = argmax p(D|h) h属于集合H
---------------------------