🎯要点
🎯算法池化和最佳分区搜索:🖊网格搜索 | 🖊发现算法池 | 🖊返回指定图的最佳划分 | 🖊返回指定图的最佳分区 | 🎯适应度和聚类比较功能:🖊图的划分 | 🖊节点度 | 🖊给定算法检测到社群总数 | 🖊图密度 | 🖊社群顶点的度数之和 | 🖊解之间的预期一致 | 🖊联合熵 | 🖊平均内部度、所有可能的节点对的平均路径长度 | 🖊节点指向社群外的边平均比例 | 🖊现有边距离社群比例 | 社群内部密度 | 🖊切割比率的标准化变体 | 🖊边超几何分布随机出现的统计方法 | 🖊兰德指数预测聚类之间的相似性度量 | 分区之间最佳匹配的平均 F1 分数 | 归一化互信息
📜图算法用例
📜Python和MATLAB网络尺度结构和幂律度大型图生成式模型算法
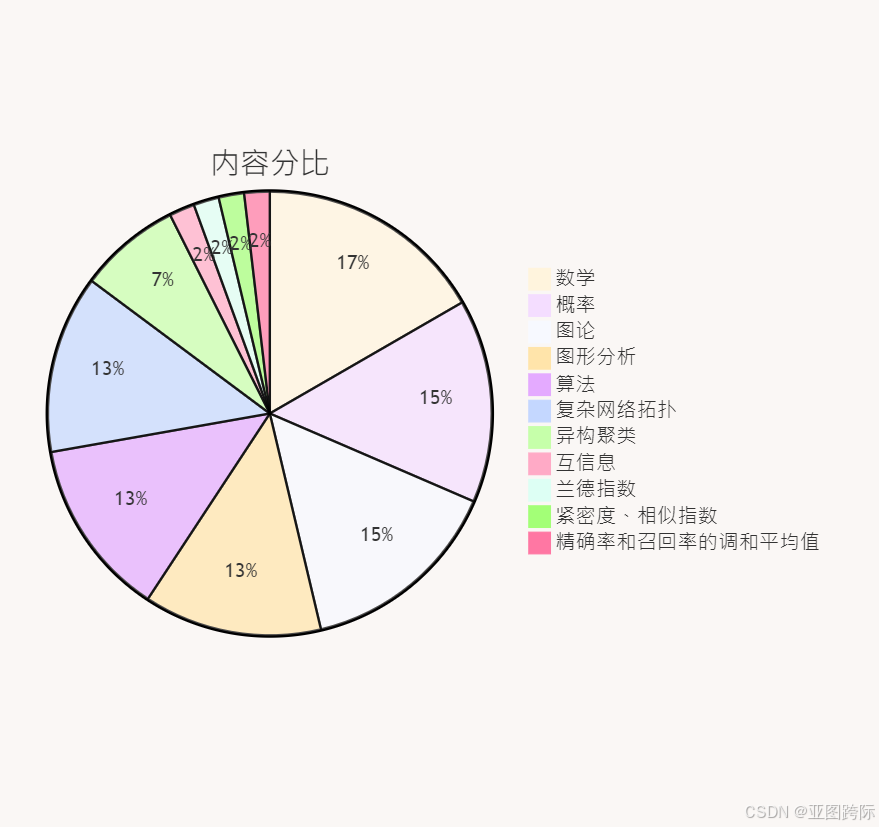
🍪语言内容分比
🍇Python和MATLAB异构网络算法
异构信息网络是一种网络结构,其对象可以假设不同的对象类型,对象之间的链接可以表示对象之间的不同类型的关系。此网无处不在,用于对许多不同类型的现实世界数据进行建模。例如,社交软件开放图将用户、帖子、事件和页面建模为四种不同类型的对象。用户可以发布帖子、参加活动或喜欢页面,这说明了将用户对象与帖子相关联的三种不同类型的连接。
此网络数据分析一直是一个活跃的研究领域。作为机器学习和数据挖掘的一项基本任务,聚类分析在此网络中找到了有趣的应用。例如,根据社交软件用户的兴趣对其进行聚类,可以实现有效的目标营销和病毒式营销。
谱聚类将聚类转化为图分割问题,该问题优化衡量分割质量的某个标准,例如正则化切割。通常,给定一组对象 X = { x 1 , x 2 , … , x n } X=\left\{x_1, x_2, \ldots, x_n\right\} X={x1,x2,…,xn},标准谱聚类方法首先构造一个无向图 G = ( X , S ) G=(X, S) G=(X,S),其中 X X X 表示顶点集, S S S 是一个矩阵, S i j S_{i j} Sij 度量对象 x i x_i xi 和 x j x_j xj 之间的相似性。然后,计算拉普拉斯矩阵 L S L_S LS,在此基础上执行特征分解以获得与 k k k 个最小特征值相对应的 k k k 个特征向量,其中 k k k 是所需的聚类数量。这些特征向量被用作对象的新特征空间。最后,应用后处理步骤,例如 k k k 均值和光谱旋转将对象划分为 k k k 个聚类。
异构信息网络:
令 T = { T 1 , … , T m } T =\left\{T_1, \ldots, T_m\right\} T={T1,…,Tm} 为一组 m m m 对象类型。对于每种类型 T i T_i Ti,令 X i X _i Xi 为类型 T i T_i Ti 的对象集。 异构信息网络是一个图 G = ( V , E ) G =( V , E ) G=(V,E),其中 V = ⋃ i = 1 m X i V =\bigcup_{i=1}^m X _i V=⋃i=1mXi 是一组节点, E E E 是一组链接,每个链接代表一个二进制 V V V 中两个对象之间的关系。
它的网络模式:
网络模式是异构信息网络 G = ( V , E ) G =( V , E ) G=(V,E) 的元模板。令 (1) ϕ : V → T \phi: V \rightarrow T ϕ:V→T 为对象类型映射,将 V V V 中的对象映射为其类型,(2) ψ : E → R \psi: E \rightarrow R ψ:E→R 为链接关系映射将 E E E 中的链接映射到一组关系 R R R 中的关系。异构信息网络 G G G 的网络模式用 T G = ( T , R ) T_{ G }=( T , R ) TG=(T,R) 表示,显示了不同类型的对象如何通过 R R R 中的关系进行关联。使用示意图来表示 T G T_{G} TG,其中 T T T和 R R R分别为节点集和边集。具体来说,示意图中存在一条边 ( T i , T j ) \left(T_i, T_j\right) (Ti,Tj) ,前提是 R R R 中存在将 T i T_i Ti 类型的对象与 T j T_j Tj 类型的对象相关联的关系。
算法
谱聚类的关键步骤是构建高质量的相似度矩阵
S
S
S。对于异构信息网络,元路径已被有效地用于测量对象相似性。例如,给定元路径
P
P
P,PathSim测量两个对象
x
u
x_u
xu 和
x
v
x_v
xv 之间的相似度。
P
P
P 通过计算连接两个对象的
P
P
P 的路径实例的数量。具体来说,我们有,
S
P
(
x
u
,
x
v
)
=
2
×
∣
{
p
x
u
⇝
x
v
:
p
x
u
⇝
x
v
⊢
P
}
∣
∣
{
p
x
u
⇝
x
u
:
p
x
u
→
x
u
⊢
P
}
∣
+
∣
{
p
x
v
⇝
x
v
:
p
x
v
⇝
x
v
⊢
P
}
∣
.
S_{ P }\left(x_u, x_v\right)=\frac{2 \times\left|\left\{p_{x_u \rightsquigarrow x_v}: p_{x_u \rightsquigarrow x_v} \vdash P \right\}\right|}{\left|\left\{p_{x_u \rightsquigarrow x_u}: p_{x_u \rightarrow x_u} \vdash P \right\}\right|+\left|\left\{p_{x_v \rightsquigarrow x_v}: p_{x_v \rightsquigarrow x_v} \vdash P \right\}\right|} .
SP(xu,xv)=∣{pxu⇝xu:pxu→xu⊢P}∣+∣{pxv⇝xv:pxv⇝xv⊢P}∣2×∣{pxu⇝xv:pxu⇝xv⊢P}∣.
给定一组元路径
P
S
P S
PS,每个元路径
P
i
∈
P
S
P _i \in P S
Pi∈PS 根据上式导出相似性矩阵
S
P
i
S_{ P _i}
SPi。我们构造一个矩阵
W
W
W 作为以下各项的加权和:矩阵:
W
=
∑
i
=
1
∣
P
S
∣
λ
i
S
P
i
.
W=\sum_{i=1}^{| P S |} \lambda_i S_{ P _i} .
W=i=1∑∣PS∣λiSPi.
优化
由于约束
rank
(
L
S
)
=
n
−
k
\operatorname{rank}\left(L_S\right)=n-k
rank(LS)=n−k,优化问题是非凸的。因此很难直接优化问题。我们将原问题转化为:
min
∥
S
−
∑
i
=
1
∣
P
S
∣
λ
i
S
P
i
∥
F
2
+
α
∥
S
∥
F
2
+
β
∥
λ
∥
2
2
+
2
γ
∑
i
=
1
k
σ
i
(
L
S
)
,
s.t.
∑
j
=
1
n
S
i
j
=
1
,
S
i
j
≥
0
,
∑
i
=
1
∣
P
S
∣
λ
i
=
1
,
λ
i
≥
0
,
\begin{aligned} & \min \left\|S-\sum_{i=1}^{| P S |} \lambda_i S_{ P _i}\right\|_F^2+\alpha\|S\|_F^2+\beta\| \lambda \|_2^2+2 \gamma \sum_{i=1}^k \sigma_i\left(L_S\right), \\ & \text { s.t. } \sum_{j=1}^n S_{i j}=1, S_{i j} \geq 0, \sum_{i=1}^{| P S |} \lambda_i=1, \lambda_i \geq 0, \end{aligned}
min
S−i=1∑∣PS∣λiSPi
F2+α∥S∥F2+β∥λ∥22+2γi=1∑kσi(LS), s.t. j=1∑nSij=1,Sij≥0,i=1∑∣PS∣λi=1,λi≥0,
其中
σ
i
(
L
S
)
\sigma_i\left(L_S\right)
σi(LS)表示
L
S
L_S
LS的第
i
i
i个最小特征值。由于
L
S
L_S
LS是半定的,
σ
i
(
L
S
)
≥
0
\sigma_i\left(L_S\right)\geq 0
σi(LS)≥0。通过设置较大的
γ
\gamma
γ 值,我们将
∑
i
=
1
k
σ
i
(
L
S
)
\sum_{i=1}^k \sigma_i\left(L_S\right)
∑i=1kσi(LS) 强制为零,以保证
rank
(
L
S
)
)
=
n
−
k
\operatorname{rank}\left(L_S\right) )=n-k
rank(LS))=n−k。根据凯-范定理,我们有,
∑
i
=
1
k
σ
i
(
L
S
)
=
min
F
∈
R
n
×
k
,
F
T
F
=
I
tr
(
F
T
L
S
F
)
\sum_{i=1}^k \sigma_i\left(L_S\right)=\min _{F \in R ^{n \times k}, F^T F=I} \operatorname{tr}\left(F^T L_S F\right)
i=1∑kσi(LS)=F∈Rn×k,FTF=Imintr(FTLSF)
其中
tr
(
⋅
)
\operatorname{tr}(\cdot)
tr(⋅) 是跟踪运算符。因此优化问题等价于:
min
∥
S
−
∑
i
=
1
∣
P
S
∣
λ
i
S
P
i
∥
F
2
+
α
∥
S
∥
F
2
+
β
∥
λ
∥
2
2
+
2
γ
tr
(
F
T
L
S
F
)
,
s.t.
∑
j
=
1
n
S
i
j
=
1
,
S
i
j
≥
0
,
∑
i
=
1
∣
P
S
∣
λ
i
=
1
,
λ
i
≥
0
,
F
∈
R
n
×
k
,
F
T
F
=
I
,
\begin{aligned} & \min \left\|S-\sum_{i=1}^{| P S |} \lambda_i S_{ P _i}\right\|_F^2+\alpha\|S\|_F^2+\beta\| \lambda \|_2^2+2 \gamma \operatorname{tr}\left(F^T L_S F\right), \\ & \text { s.t. } \sum_{j=1}^n S_{i j}=1, S_{i j} \geq 0, \sum_{i=1}^{| P S |} \lambda_i=1, \lambda_i \geq 0, F \in R ^{n \times k}, F^T F=I, \end{aligned}
min
S−i=1∑∣PS∣λiSPi
F2+α∥S∥F2+β∥λ∥22+2γtr(FTLSF), s.t. j=1∑nSij=1,Sij≥0,i=1∑∣PS∣λi=1,λi≥0,F∈Rn×k,FTF=I,
Python伪代码实现算法:
from sklearn.cluster import KMeans
import numpy as np
from scipy.optimize import minimize
class alg:
def __init__(self, similarity_matrices, num_clusters, random_seed=0):
self.num_clusters = num_clusters
self.random_seed = random_seed
self.num_nodes = None
self.similarity_matrices = []
self.metapath_index = {}
self.alpha = None
self.beta = None
self.gamma = None
for index, (metapath, matrix) in enumerate(similarity_matrices.items()):
if self.num_nodes is None:
self.num_nodes = matrix.shape[0]
if matrix.shape != (self.num_nodes, self.num_nodes):
raise ValueError('Invalid shape of similarity matrix.')
row_normalized_matrix = matrix/matrix.sum(axis=1, keepdims=True)
self.similarity_matrices.append(row_normalized_matrix)
self.metapath_index[metapath] = index
self.similarity_matrices = np.array(self.similarity_matrices)
self.num_metapaths = len(similarity_matrices)
def run(self, verbose=False, cluster_using='similarity'):
if cluster_using not in ['similarity', 'laplacian']:
raise ValueError('Invalid option for parameter \'cluster_using\'.')
similarity_matrix, metapath_weights = self.optimize(verbose=verbose)
if cluster_using == 'similarity':
labels = self.cluster(similarity_matrix)
elif cluster_using == 'laplacian':
laplacian = normalized_laplacian(similarity_matrix)
labels = self.cluster(eigenvectors(laplacian, num=self.num_clusters))
metapath_weights_dict = {metapath: metapath_weights[index] for metapath, index in self.metapath_index.items()}
return labels, similarity_matrix, metapath_weights_dict
def cluster(self, feature_matrix):
return KMeans(self.num_clusters, n_init=10, random_state=self.random_seed).fit_predict(feature_matrix)
def optimize(self, num_iterations=20, alpha=0.5, beta=10, gamma=0.01, verbose=False):
self.alpha = alpha
self.beta = beta
self.gamma = gamma
lambdas = np.ones(self.num_metapaths)/self.num_metapaths
W = np.tensordot(lambdas, self.similarity_matrices, axes=[[0], [0]])
S = W
for iteration in range(num_iterations):
if verbose:
loss = np.trace(np.matmul((S - W).T, (S - W)))
loss += self.alpha * np.trace(np.matmul(S.T, S))
loss += self.beta * np.dot(lambdas, lambdas)
loss += self.gamma * np.sum(eigenvalues(normalized_laplacian(S), num=self.num_clusters))
print('Iteration %d: Loss = %0.3f' % (iteration, loss))
F = self.optimize_F(S)
S = self.optimize_S(W, F)
lambdas = self.optimize_lambdas(S, lambdas)
W = np.tensordot(lambdas, self.similarity_matrices, axes=[[0], [0]])
return S, lambdas
def optimize_F(self, S):
LS = normalized_laplacian(S)
return eigenvectors(LS, num=self.num_clusters)
def optimize_S(self, W, F):
Q = distance_matrix(F, metric='euclidean')
P = (2*W - self.gamma*Q)/(2 + 2*self.alpha)
S = np.zeros((self.num_nodes, self.num_nodes))
for index in range(S.shape[0]):
S[index] = best_simplex_projection(P[index])
return S
def optimize_lambdas(self, S, init_lambdas):
def objective(lambdas):
W = np.tensordot(lambdas, self.similarity_matrices, axes=[[0], [0]])
value = np.trace(np.matmul(W.T, W))
value -= 2 * np.trace(np.matmul(S.T, W))
value += self.beta * np.dot(lambdas, lambdas)
return value
def constraints():
def sum_one(lambdas):
return np.sum(lambdas) - 1
return {
'type': 'eq',
'fun': sum_one,
}
def bounds(init_lambdas):
return [(0, 1) for init_lambda in init_lambdas]
return minimize(objective, init_lambdas, method='SLSQP', constraints=constraints(), bounds=bounds(init_lambdas)).x
MATLAB伪代码算法实现:
function [y, S, evs, A] = alg(mp_matrix, c, true_cluster)
NITER = 20;
zr = 10e-11;
alpha = 0.5;
beta = 10;
gamma = 0.01;
P = size(mp_matrix,1);
n = size(mp_matrix,2);
lambda = ones(P,1)./P;
eps = 1e-10;
A0 = zeros(n,n);
for p = 1:P
A0 = A0 + lambda(p) * squeeze(mp_matrix(p,:,:));
end;
A0 = A0-diag(diag(A0));
A10 = (A0+A0')/2;
D10 = diag(sum(A10));
L0 = D10 - A10;
[F0, ~, evs]=eig1(L0, n, 0);
F = F0(:,1:c);
[pred] = postprocess(F,c,true_cluster);
for iter = 1:NITER
dist = L2_distance_1(F',F');
S = zeros(n);
for i=1:n
a0 = A0(i,:);
idxa0 = 1:n;
ai = a0(idxa0);
di = dist(i,idxa0);
ad = (ai-0.5*gamma*di)/(1+alpha); S(i,idxa0) = EProjSimplex_new(ad);
end;
A = S;
A = (A+A')/2;
D = diag(sum(A));
L = D-A;
F_old = F;
[F, ~, ev]=eig1(L, c, 0);
[pred] = postprocess(F,c,true_cluster);
evs(:,iter+1) = ev;
fn1 = sum(ev(1:c));
fn2 = sum(ev(1:c+1));
lambda_old = lambda;
if fn1 > zr
gamma = 2*gamma;
lambda = optimizeLambda(mp_matrix, S, beta); % optimize lambda
elseif fn2 < zr
gamma = gamma/2; F = F_old; lambda = lambda_old;
else
break;
end;
A0 = zeros(n,n);
for p = 1:P
A0 = A0 + lambda(p) * squeeze(mp_matrix(p,:,:));
end;
end;
[clusternum, y]=graphconncomp(sparse(A)); y = y';
nmi = calculateNMI(y,true_cluster);
purity = eval_acc_purity(true_cluster,y);
ri = eval_rand(true_cluster,y);
fprintf('Final NMI is %f\n',nmi);
fprintf('Final purity is %f\n',purity);
fprintf('Final rand is %f\n',ri);
if clusternum ~= c
sprintf('Can not find the correct cluster number: %d', c)
end;