深度寻路算法（含图形化界面）--------C语言

深度寻路算法思想：

文章目录

规定试探方向：上右下左上左下右
实时记录每个点，当前试探方向
- 并且确定每个点是否已经走过
回退：
- 每走一步，存储一下当前点的位置（利用栈结构）
- 等到需要回退的时候，出栈，返回当前栈顶元素，让当前点返回到上一个
遇到终点，栈结构存储从开始到终点的路径，如果整个栈为空，说明没有终点

1. 深度寻路语言描述

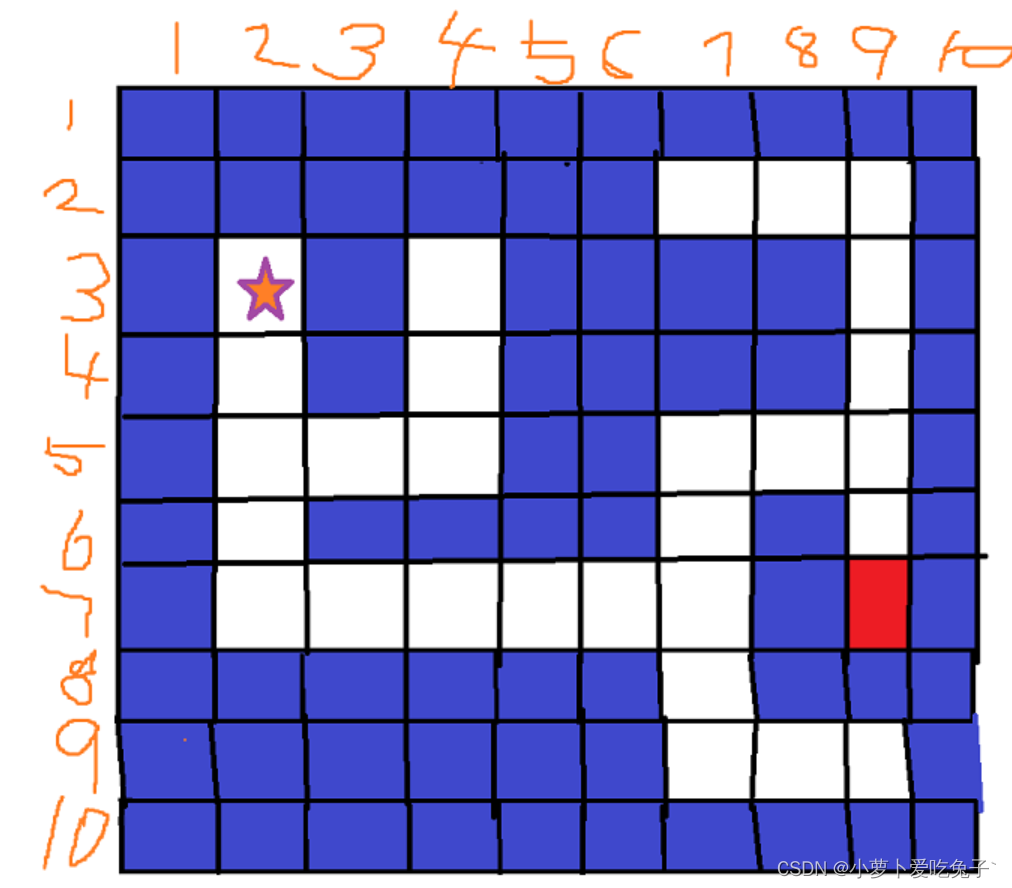
在这里插入图片描述
如图：我们在起点（2，3）的位置，要到达终点为（9，7）的位置：紫色为墙壁法无移动，白色为路径

已经走过的路会被标记为true，表示已走过，不可以重复再走一遍；没有走的为false，表示可以行走

起始点为（2，3）；试探点（下一步将要移动的一个临时点）为（2，3）;

试探方向 ：顺时针 上右下左（优先按照顺序通行）

首先我们在起点试探上方向，为墙壁，所以我们无法移动。我们接着试探右方向，发现也为墙壁，无法移动。接着试探下方向，可以移动，则当前位置移动到（2，4）的位置。
接着在新的位置在重新开始上右下左的方向遍历，可以得到，继续往下移动，到达（2，5）
接着往右移动，往右移动，往右移动，往上移动，往上移动，注意：此时到达（4，3）的位置，但是！！！这个地方是一个死胡同。请注意我们无法实现自主回退，因为我们无法重新行走已经走过的路径！！
那这样要怎么办呢，我们用到了***栈回退的功能***，我们用一个栈来存储每一步的x，y坐标，栈顶元素即为当前的位置，我们到达死胡同时，会执行出栈操作，因为出栈会实现回退，这样我们的位置就回退到了（4，4）
注意我们此时依旧是死胡同，因为只有一条路，走过的路不能重复走，所以我们必须继续栈回退，直到我们退到了一个可以继续走的位置：（2，5）（是一个十字路口），第一次我们往右走，走不通，所以这次我们会跳过右的路径，进行往下的移动，移动到（2，6），接着往下，往右，往右… 一个重复的步骤

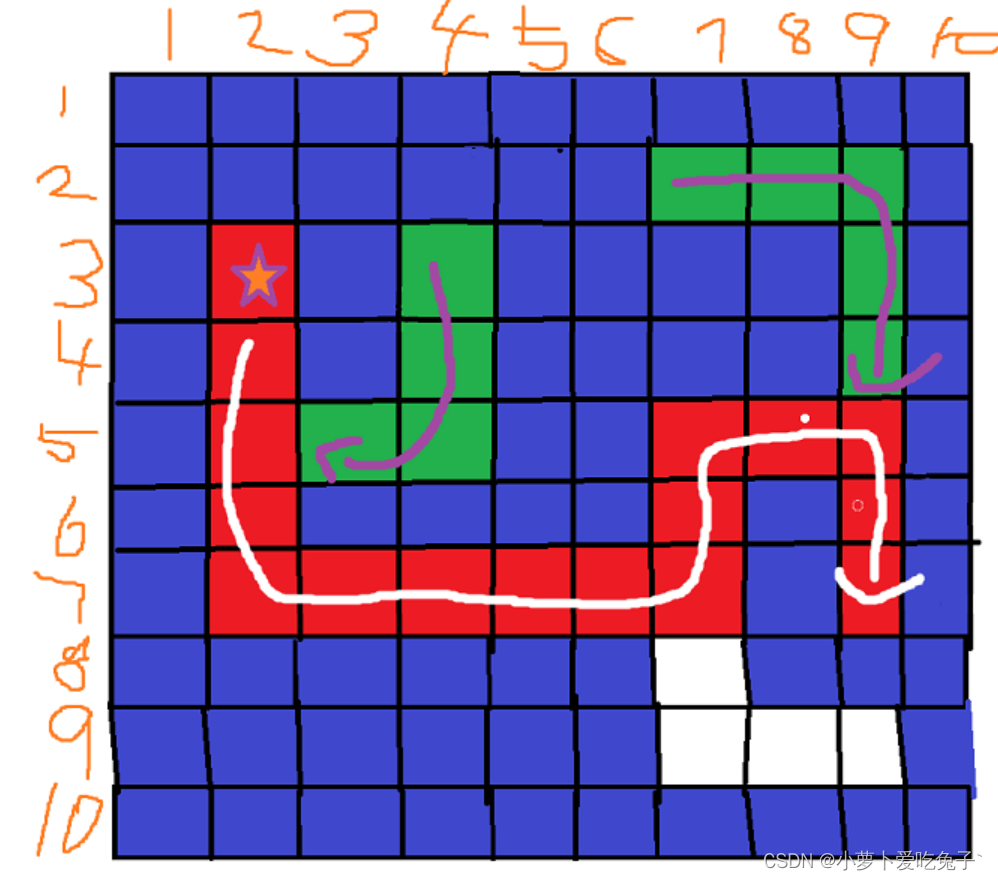
总结：红色的路径表示最终所走的路径，绿色路径表示走到了死胡同进行栈回退的路径；

在多个方向均可以移动的情况下，按上右下左优先通行，
在这里插入图片描述

2. 栈结构的准备

我们需要一个栈来存储所经过路径，这里采用了顺序栈的形式，当然也可以采用链式栈的形式，栈结构必须要有 入栈出栈获取栈顶元素判断栈是否为空等操作
关于栈和队列的详细操作，请看我这篇博文

#pragma once
#include <iostream>
#include <string.h>
#include <stdlib.h>
#include <malloc.h>
#include <string.h>
using namespace std;
template<class T>
class MyVector
{
	T*			pArr;		//保存顺序表的首地址
	size_t		len;		//顺序表元素个数
	size_t		capacity;	//当前容量
public:
	MyVector();
	~MyVector();

	//入栈
	void push(const T& data);
	//出栈
	void pop()
	{
		if (len > 0)
		{
			len--;
		}
	}
	//获取栈顶元素
	T GetTop()
	{
		return pArr[len-1];
	}
	//判断是否为空
	bool isempty()
	{
		return len == 0;
	}
};
template<class T>
MyVector<T>::MyVector(){
	pArr = NULL;
	capacity = len = 0;
}
template<class T>
MyVector<T>::~MyVector(){
	if (pArr){
		delete[] pArr;
	}
	pArr = NULL;
	capacity = len = 0;
}
//入栈
template<class T>
void MyVector<T>::push(const T& data){
	//1.开辟新的内存区域
	if (pArr == NULL)
	{
		//1. 开辟新的空间
		T* pNew = (T*)malloc(sizeof(T) * (len + 1));
		//2. 原来的内存指向新的开辟的内存
		pArr = pNew;
		//3. 插入数据
		pArr[len++] = data;
	}
	else
	{
		//1.为后面的开辟新的内存
		T* pNew = (T*)malloc(sizeof(T) * (len + 1));
		//2.将原有的内存数据的元素拷贝到新的内存里
		memcpy(pNew, pArr, sizeof(T) * len);
		//3.释放原有的内存空间
		free(pArr);
		//4.原来的内存指向新的开辟的内存
		pArr = pNew;
		//5.插入数据
		pArr[len++] = data;
	}
	return;
}

3. 深度寻路算法的实现：

准备一个地图和一个辅助地图

地图：

#define ROW 10
#define COL 10

int map[ROW][COL] =
	{
		{1,1,1,1,1,1,1,1,1,1},
		{1,0,1,0,1,1,1,1,1,1},
		{1,0,1,0,0,0,0,0,1,1},
		{1,0,1,0,1,1,1,0,1,1},
		{1,0,0,0,1,1,1,1,1,1},
		{1,1,1,0,0,0,1,1,1,1},
		{1,1,1,0,1,1,0,0,0,1},
		{1,1,1,0,1,0,0,1,1,1},
		{1,1,1,0,0,0,1,1,1,1},
		{1,1,1,1,1,1,1,1,1,1},
	};

辅助地图：

enum Direct
{
	p_up,
	p_right,
	p_down,
	p_left,
};

struct pathNode
{
	int dir;		//方向 0  
	bool isFind;	//是否走过 false  0没有走过
};	
struct Mypoint
{
	int row;
	int col;
	//重载==运算符，为接下来的判断是否到达终点做准备
	bool operator==(const Mypoint& pos)
	{
		if (row == pos.row && col == pos.col)
		{
			return true;
		}
		return false;
	}
};

辅助地图有一个结构体，记录每个位置的初始方向与是否走过，我们可以设置一个方向枚举，上右下左分别表示0 1 2 3 ；是否走过的标记设置为false 即0；那么我们就可以迅速的给这个辅助地图赋值，即：

//辅助地图
pathNode pathMap[ROW][COL] = { 0 };

确定初始点与试探点，终点:

Mypoint结构体记录每个点的位置即 row和col x和y的坐标

	//起始点坐标
	Mypoint Begpos = { 1,1 };
	//终点坐标
	Mypoint Endpos = { 6,8 };
	//当前点
	Mypoint Curpos = Begpos;
	//试探点
	Mypoint Researchpos;

起点坐标入栈

	//起点坐标入栈
	MyVector<Mypoint> pStack;
	pStack.push(Curpos);
	//起点位置设置为true 已经走过
	pathMap[Curpos.row][Curpos.col].isFind = true;

循环寻路

寻路过程：来一个循环：由当前点的方向来决定他往哪里走；如果往一个方向走，则试探点先走，更新当前点方向（因为无论如何你的方向都要依次增加）；判断试探点的信息能否走，如果为false并且为0；说明能走，就走，更新当前点的位置为试探点；当前点位置入栈；记录当前点坐标为true，表示已经走过，下次不能走，只能通过退栈的形式返回

注意：上右下这第三个的case语句内容基本是一致的，只有试探点的坐标更新不同，理解了一个则剩下的很容易理解
当到达最后一个方向，即左时，如果还不能走，说明死胡同，则需要执行退栈操作，让当前点位置回退到上一个位置，直到到达了一个可以重复走的位置，注意执行顺序：先出栈再获取栈顶元素
最后，如果终点的坐标等于当前点的坐标，说明到达终点，记得重载==运算符
如果最后栈为空，说明路径没有终点，因为到达死胡同会一直退栈，如果退栈到栈为空，说明整条路没有可以走的路了，则没有终点

while (1)
	{
		//试探点重新更新
		Researchpos = Curpos;
		switch (pathMap[Curpos.row][Curpos.col].dir)
		{
		case p_up:
			//试探点的坐标更新
			Researchpos.row--;
			//无论是否能走，它的方向肯定要改变
			pathMap[Curpos.row][Curpos.col].dir++;
			if (pathMap[Researchpos.row][Researchpos.col].isFind == false &&
				map[Researchpos.row][Researchpos.col] == 0)
			{
				//能走  就走
				Curpos = Researchpos;
				//当前点位置入栈
				pStack.push(Curpos);
				//当前点标记已经走过
				pathMap[Curpos.row][Curpos.col].isFind = true;
			}
			break;
		case p_right:
			//试探点的坐标更新
			Researchpos.col++;
			//无论是否能走，它的方向肯定要改变
			pathMap[Curpos.row][Curpos.col].dir++;
			if (pathMap[Researchpos.row][Researchpos.col].isFind == false &&
				map[Researchpos.row][Researchpos.col] == 0)
			{
				//能走  就走
				Curpos = Researchpos;
				//当前点位置入栈
				pStack.push(Curpos);
				//当前点标记已经走过
				pathMap[Curpos.row][Curpos.col].isFind = true;
			}
			break;
		case p_down:
			//试探点的坐标更新
			Researchpos.row++;
			//无论是否能走，它的方向肯定要改变
			pathMap[Curpos.row][Curpos.col].dir++;
			if (pathMap[Researchpos.row][Researchpos.col].isFind == false &&
				map[Researchpos.row][Researchpos.col] == 0)
			{
				//能走  就走
				Curpos = Researchpos;
				//当前点位置入栈
				pStack.push(Curpos);
				//当前点标记已经走过
				pathMap[Curpos.row][Curpos.col].isFind = true;
			}
			break;
		case p_left:
			//试探点的坐标更新
			Researchpos.col--;
			无论是否能走，它的方向肯定要改变
			//pathMap[Curpos.row][Curpos.col].dir++;
			if (pathMap[Researchpos.row][Researchpos.col].isFind == false &&
				map[Researchpos.row][Researchpos.col] == 0)
			{
				//能走  就走
				Curpos = Researchpos;
				//当前点位置入栈
				pStack.push(Curpos);
				//当前点标记已经走过
				pathMap[Curpos.row][Curpos.col].isFind = true;
			}
			else	//死胡同，执行回退操作
			{
				//到达最后一个方向还是没有出去，说明是死胡同 
				//执行出栈操作
				pStack.pop();
				//获取栈顶元素
				Curpos = pStack.GetTop();
			}
			break;
		}
		//是否到达终点
		if (Endpos == Curpos)
		{
			isFindEnd = true;
			break;
		}
		//没有到达终点
		if (pStack.isempty())
		{
			printf("这条路没有终点!\n");
			return 0;
		}
	}

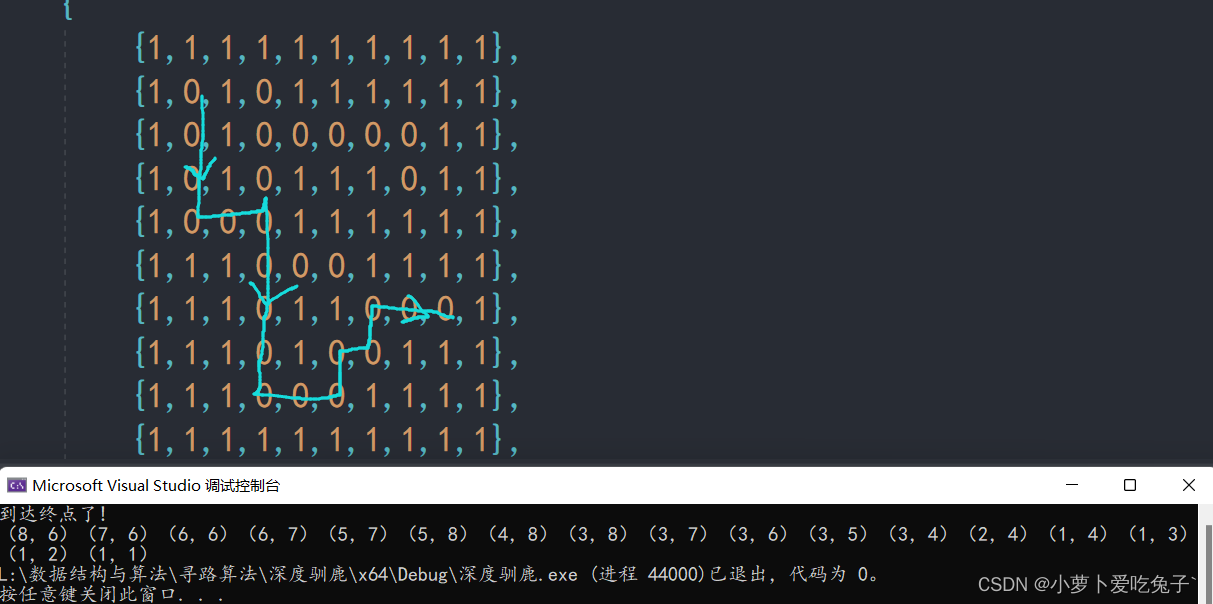
简单测试寻路过程

到达终点后依次从后往前退栈，打印出路径情况

int x, y;
	if (isFindEnd)
	{
		//到达终点
		printf("到达终点了!\n");
		while (!pStack.isempty())
		{
			x=pStack.GetTop().col;
			y = pStack.GetTop().row;
			printf("（%d，%d）", x, y);
			pStack.pop();
		}
	}

在这里插入图片描述

4. 深度寻路完整代码

包含寻路的图形化界面
具体素材请点击这里

#include "MyVector.h"
#include <Windows.h>
#include <graphics.h>

#define ROW 10
#define COL 10
#define SIZE 50
enum Direct
{
	p_up,
	p_right,
	p_down,
	p_left,
};

struct pathNode
{
	int dir;		//方向 0  
	bool isFind;	//是否走过 false  0没有走过
};

struct Mypoint
{
	int row;
	int col;
	bool operator==(const Mypoint& pos)
	{
		if (row == pos.row && col == pos.col)
		{
			return true;
		}
		return false;
	}
};

#if 1
IMAGE road, wall, pos, ren;
void printmapCMD(int(*map)[COL], Mypoint pos);
void printmapDRAW(int(*map)[COL], Mypoint pos);
void load_IMAGE();
int main()
{
	int map[ROW][COL] =
	{
		{1,1,1,1,1,1,1,1,1,1},
		{1,0,1,0,1,0,0,1,1,1},
		{1,0,1,0,1,1,1,0,1,1},
		{1,0,1,0,1,1,1,0,1,1},
		{1,0,0,0,1,1,1,0,1,1},
		{1,1,1,0,0,0,1,0,1,1},
		{1,1,1,0,1,1,0,0,0,1},
		{1,1,1,0,1,0,0,1,1,1},
		{1,1,1,0,0,0,1,1,1,1},
		{1,1,1,1,1,1,1,1,1,1},
	};
	//辅助地图
	pathNode pathMap[ROW][COL] = { 0 };

	load_IMAGE();
	setbkcolor(WHITE);
	cleardevice();


	//起始点坐标
	Mypoint Begpos = { 1,1 };
	//终点坐标
	Mypoint Endpos = { 7,2 };
	//当前点
	Mypoint Curpos = Begpos;
	//试探点
	Mypoint Researchpos;
	//起点坐标入栈
	MyVector<Mypoint> pStack;
	pStack.push(Curpos);
	//起点位置设置为true 走过
	pathMap[Curpos.row][Curpos.col].isFind = true;

	//是否到达终点
	bool isFindEnd = false;

	while (1)
	{
		//试探点重新更新
		Researchpos = Curpos;
		switch (pathMap[Curpos.row][Curpos.col].dir)
		{
		case p_up:
			//试探点的坐标更新
			Researchpos.row--;
			//无论是否能走，它的方向肯定要改变
			pathMap[Curpos.row][Curpos.col].dir++;
			if (pathMap[Researchpos.row][Researchpos.col].isFind == false &&
				map[Researchpos.row][Researchpos.col] == 0)
			{
				//能走  就走
				Curpos = Researchpos;
				//当前点位置入栈
				pStack.push(Curpos);
				//当前点标记已经走过
				pathMap[Curpos.row][Curpos.col].isFind = true;
			}
			break;
		case p_right:
			//试探点的坐标更新
			Researchpos.col++;
			//无论是否能走，它的方向肯定要改变
			pathMap[Curpos.row][Curpos.col].dir++;
			if (pathMap[Researchpos.row][Researchpos.col].isFind == false &&
				map[Researchpos.row][Researchpos.col] == 0)
			{
				//能走  就走
				Curpos = Researchpos;
				//当前点位置入栈
				pStack.push(Curpos);
				//当前点标记已经走过
				pathMap[Curpos.row][Curpos.col].isFind = true;
			}
			break;
		case p_down:
			//试探点的坐标更新
			Researchpos.row++;
			//无论是否能走，它的方向肯定要改变
			pathMap[Curpos.row][Curpos.col].dir++;
			if (pathMap[Researchpos.row][Researchpos.col].isFind == false &&
				map[Researchpos.row][Researchpos.col] == 0)
			{
				//能走  就走
				Curpos = Researchpos;
				//当前点位置入栈
				pStack.push(Curpos);
				//当前点标记已经走过
				pathMap[Curpos.row][Curpos.col].isFind = true;
			}
			break;
		case p_left:
			//试探点的坐标更新
			Researchpos.col--;
			无论是否能走，它的方向肯定要改变
			//pathMap[Curpos.row][Curpos.col].dir++;
			if (pathMap[Researchpos.row][Researchpos.col].isFind == false &&
				map[Researchpos.row][Researchpos.col] == 0)
			{
				//能走  就走
				Curpos = Researchpos;
				//当前点位置入栈
				pStack.push(Curpos);
				//当前点标记已经走过
				pathMap[Curpos.row][Curpos.col].isFind = true;
			}
			else
			{
				//到达最后一个方向还是没有出去，说明是死胡同 
				//执行出栈操作
				pStack.pop();
				Curpos = pStack.GetTop();
			}
			break;
		}

		printmapCMD(map, Curpos);
		printmapDRAW(map, Curpos);
		//是否到达终点
		if (Endpos == Curpos)
		{
			isFindEnd = true;
			break;
		}
		//没有到达终点
		if (pStack.isempty())
		{
			printf("这条路没有终点!\n");
			return 0;
		}
	}
	int x, y;
	if (isFindEnd)
	{
		//到达终点
		printf("到达终点了!\n");
		while (!pStack.isempty())
		{
			x=pStack.GetTop().col;
			y = pStack.GetTop().row;
			printf("（%d，%d）", x, y);
			putimage(SIZE + x * SIZE, SIZE + y * SIZE, &pos);
			pStack.pop();
		}
	}
	system("pause");
	return 0;
}


#else

int main()
{
	MyVector<int> a;
	for (int i = 0; i < 10; i++)
	{
		a.push(i);
	}
	while (!a.isempty())
	{
		printf("%d ", a.GetTop());
		a.pop();
	}

	return 0;
}

#endif

void printmapDRAW(int(*map)[COL], Mypoint pos)
{
	system("cls");
	for (int i = 0; i < ROW; i++)
	{
		for (int j = 0; j < COL; j++)
		{
			if (i == pos.row && j == pos.col)
			{
				putimage(SIZE + j * SIZE, SIZE + i * SIZE, &ren);
			}
			else if (map[i][j] == 1)
			{
				putimage(SIZE + j*SIZE, SIZE + i*SIZE,&wall);

			}
			else if (map[i][j]==0)
			{
				putimage(SIZE + j * SIZE, SIZE + i * SIZE, &road);
			}
		}
		printf("\n");
	}
}

void printmapCMD(int(*map)[COL], Mypoint pos)
{
	system("cls");
	for (int i = 0; i < ROW; i++)
	{
		for (int j = 0; j < COL; j++)
		{
			if (i == pos.row && j == pos.col)
			{
				printf("人");
			}
			else if (map[i][j] == 1)
			{
				printf("墙");

			}
			else if (map[i][j] == 0)
			{
				printf("  ");
			}
		}
		printf("\n");
	}
}

void load_IMAGE()
{
	initgraph(640, 640, SHOWCONSOLE);
	loadimage(&wall, L"./wall.bmp",50,50);
	loadimage(&ren, L"./ren.bmp",50,50);
	loadimage(&pos, L"./pos.bmp",50,50);
	loadimage(&road, L"./road.bmp", 50, 50);
}