Bootstrap

高级数据结构：线段树入门（c++实现 + 详解）

文章目录

线段树概念

线段树是一种高级数据结构，与树状数组一样，被用来处理区间查询，修改问题，并且线段树的最大优点是对动态数据的处理十分高效。

关于树状数组，可以看我这篇博文的介绍：
高级数据结构：树状数组详解

来看看线段树能处理的问题：

  • 求区间的最值。给你一个区间，让你查询区间的最大值与最小值。如果用普通的数组，加上m次询问，则时间复杂度将会达到O（mn）阶，是非常低效的。
  • 区间和问题，查询，修改区间的元素，求和等等。使用普通数组对指定的区间求和，加之m次询问，则时间复杂度也会达到O（mn），也可以使用前缀和求区间和，但是前缀和虽然高效，但是远没有线段树灵活，线段树能够处理的问题是非常多的。
  • 线段树对于以上两种问题求解都具有O（nlogm）的时间复杂度，是非常高效的。

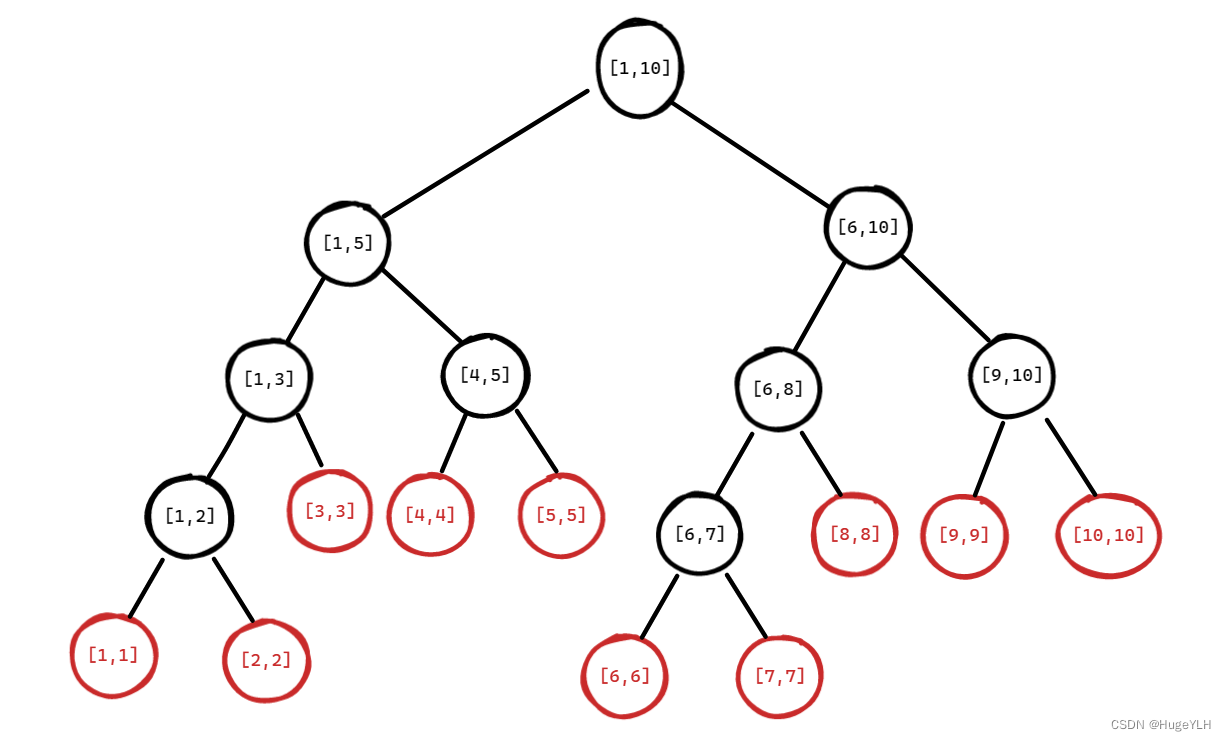
线段树是具有以下形态的二叉树，其中树上的每个节点都是一个线段区间 。

看图可以发现线段树的几个特征：

  1. 这颗二叉树是采用分治法来划分区间，并且构建子树的，左右子树各一半。

  2. 这颗二叉树的每个节点都是一个线段区间，非叶子节点的线段区间是一段不相等的区间，叶子节点的线段区间的只包含一个元素。

  3. 这颗二叉树是一颗完全二叉树（不是满二叉树），第k层有2^(k-1)个节点。
    在这里插入图片描述

线段树是一颗完全二叉树，这便是线段树做区间问题高效的原因，做查询修改问题只需要访问二叉树的指定节点，而访问节点的复杂度是O（logn）

区间最值问题

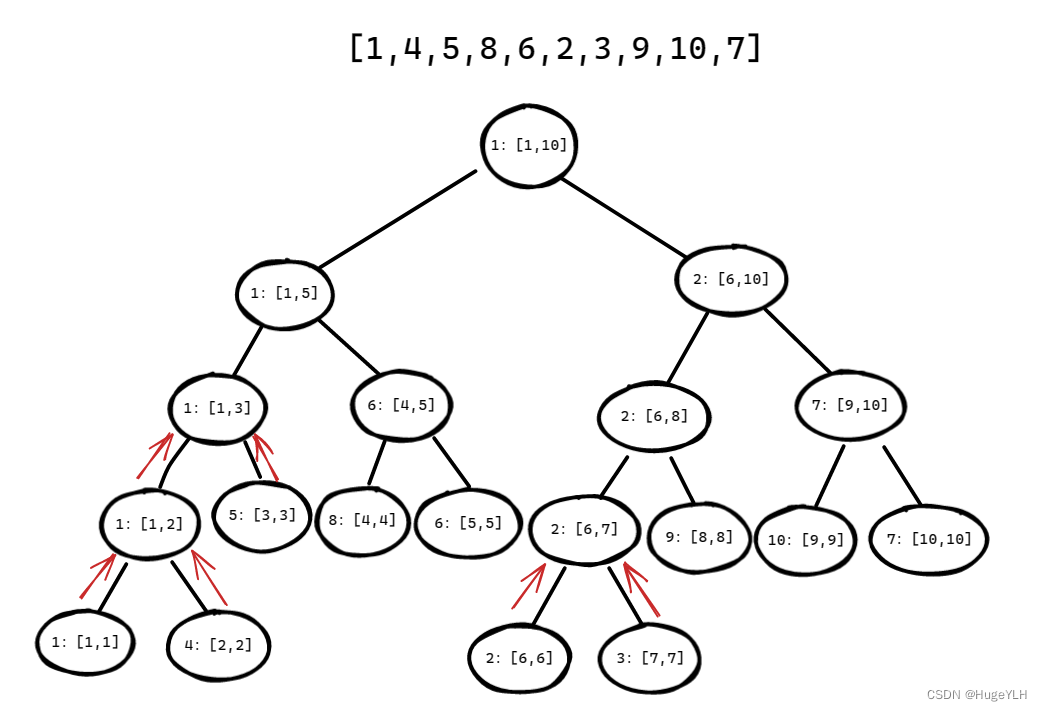
我们用区间 [1,4,5,8,6,2,3,9,10,7] 为例，来表示一颗用于查询最小值的线段树

如图所示：

节点中 1：[1，10] 的含义是在 1到10 的区间中，最小值为1

每个节点都表示一个区间，同时每一个区间的前面都记录了一个最小值
在这里插入图片描述
我们对一颗线段树提供几种操作：

  1. 辅助函数（前置准备，上移与下移）
  2. 创建线段树：build
  3. 查询线段树：query
  4. 更新线段树：update

辅助函数

在创建线段树时，我们首先要明白树的创建可以使用链式结构也可以使用顺序结构，那么我们该如何选择呢？ 可以注意到我们的线段树会经常用到查询的操作，即经常在每个节点之间进行查询，那么我们就可以通过顺序结构来更快的进行查询，同时，我们还注意到对于普通的二叉树结构满足一个重要的性质（节点序号从1开始）：已知当前节点编号为i，则其父节点编号为 i/2，其左右孩子节点编号分别为 2*i 和 2*i+1 ，即 i<<1 和 i<<1|1

所以我们的线段树准备工作如下：

  1. 使用顺序结构存储数据（数组形式）
  2. 提供访问左子树与右子树的函数（如果你够熟悉，则可以忽略此步）（我们会经常递归，利用二叉树的编号i 的性质）
  3. 向上递归时我们需要得到孩子节点的最小值来赋值给根节点一个值，我们也可以创建一个函数来完成这个功能，
const int N=100005;
int tree[N*4];		//存储线段树的数据，注意要开四倍区间，防止越界，空间浪费对于线段树是不可避免的。
inline ls(int i)
{
	return i<<1;	//访问左孩子： 2*i
}
inline rs(int i)
{
	return i<<1|1;	//访问右孩子：2*i+1
}
void push_up(int i)
{
	tree[i]=min(tree[(ls(i)],tree[rs(i)]);	//给子树的根节点值等于孩子节点的最小值
}

push_up函数的作用：
如函数名所示：上移
我们需要求区间最小值，因此当我们递归到叶子节点的时候，需要回溯，因此在回溯的过程中我们通过此函数给他们的父节点来不断更新此最小值。

创建线段树

递归创建这样一颗二叉树应该是很简单的，只需要**递归到根节点然后向上回溯（push_up）**赋值父节点即可，代码如下，我们使用build函数来创建一颗线段树。

假设我们有一个输入数组nums，保存原始的数据

void build(int i,int pl,int pr)
{
	if (pl==pr)
	{	
		tree[i]=nums[pl];
		return;
	}
	int mid=(pl+pr)>>1;	//取中间值，分治
	build(ls(i),pl,mid);	//递归左孩子
	build(rs(i),mid+1,pr);	//递归右孩子
	push_up(i);			//自底向上，给子树根节点赋值
}

查询

我们进入查询操作：

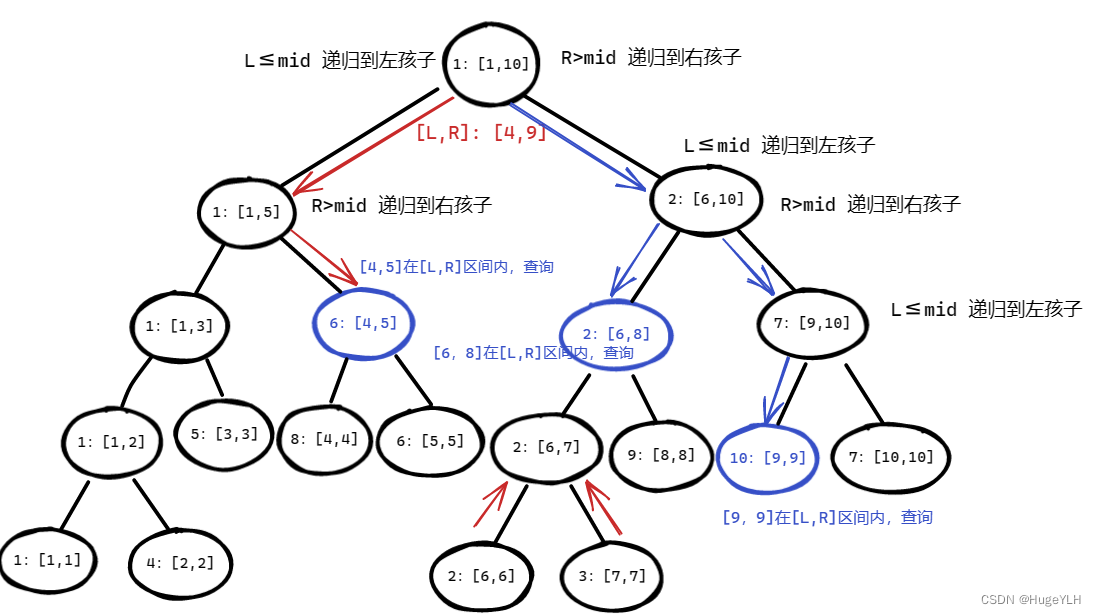
我们很容易想到，如果我们要查询 [1,3] 的最小值，则可以直接递归寻找，此时我们的运气比较好：
在我们的二叉树节点中正好就有一个节点完全包含了这个[1，3]的区间，此节点记录的最小值为1，因此得到 1到3 的最小值就是1，答案为1，查询其他 “运气比较好” 的节点也是同理。

但是如果我们要找的区间覆盖多个子区间该如何查询呢？（运气不好）

例如，我们需要查询 [ 4,9] 的最小值，但是我们发现，线段树中并没有 表示[4,9]这个区间的节点，这时我们就需要用到线段树的第一个重要性质： 分治法

我们把这个区间通过递归分治成三个子区间，分别为 [4,5] [6,8] [9,9]，我们的线段树中存在这三个子区间的节点，因此

  • 返回这三个区间记录的值，然后再取一个最小值，这就是我们所要的答案，即返回这三个区间的最小值

如何通过递归来实现到达每个节点呢，并且得到判断这个到达的这个区间节点是不是我们所需要的区间的子区间，如果是则直接返回此节点记录的最小值，如果不是，则根据我们给出的查询区间与节点区间做比较，然后判断往左子树还是往右子树递归。

关于查询：

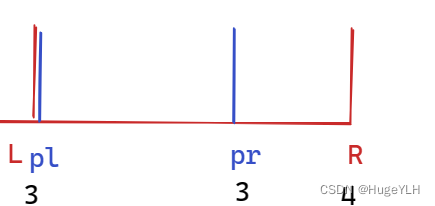
  1. 我们所要查询的区间规定为 [4,9] == [L,R] ，所以在整个查询函数中， L，R始终为4，9（这一点非常重要）
  2. mid表示树的某个节点的 （pl+pr）/2。
  • 何时递归到左孩子？
    • 当L 小于等于mid时，分治左区间，即递归以 pl 和 mid 作为子区间继续查询，递归到左孩子。
  • 何时递归到右孩子？
    • 当 R大于mid时，分治右区间，即递归 mid+1 和 pr 作为子区间继续查询，递归到右孩子。
  1. 何时结束递归？ 当pl和pr被L和R完全覆盖的时候，此时对于L和R的最小值的查询就等于pl和pr的代表的区间节点记录的最小值，如子图：注意完全覆盖指的是： L<=pl && pr<=R，注意不能是两个等于号，例如查询 [3,4]，首先根据mid与L和R递归到[3，3]区间，返回[3，3]区间的最小值；然后回溯，递归到 [4，4]区间得到其最小值，然后回溯取得两个区间的一个最小值并返回
    在这里插入图片描述

在这里插入图片描述
query查询代码实现：

int query(int i,int pl,int pr,int L,int R)
{
 	int res=-inf;
	if (L<=pl && pr<=R)
	{
		//注意《线段区间》 要完全覆盖于L，R查询区间里，此时则可以返回这个节点值，至于为什么不是双==号，看上面（5）的解释
		return tree[i];
	}
	int mid=(pl+pr)>>1;
	if (L<=mid) res=max(res,query(ls(i),pl,mid,L,R));
	if (R>mid) res=max(res,query(rs(i),mid+1,pr,L,R));
	return res;

query函数的使用：n表示原始数组的大小，对于 [1,n]的线段是从根节点1开始，查询[l,r]的最小值

  • 查询模板：query(1,1,n,l,r)

更新

关于此题使用的是简单形式的update函数，只能用于增加一个节点或者修改一个节点
在此例中我们只需求得区间最小值，无需修改区间值，因此我们可以不使用更新函数。

update函数在之后讲解区间和问题在来详细说明，update函数实际上在修改区间与查询区间的问题上非常有用，在一会我们再详细解释。

简单形式的update：

void update(int i, int pl, int pr, int L, int R, int d)
{
	if (L <= pl && pr <= R)
	{
		//找到了被完全覆盖的子区间，修改线段节点的值
		tree[i] = d;
		return;
	}
	//同build构建线段树的原理时候
	int mid = (pl + pr) >> 1;
	if (L <= mid) update(ls(i), pl, mid, L, R, d);
	if (R > mid) update(rs(i), mid + 1, pr, L, R, d);
	push_up(i);
}

update的使用

  • 更新区间最值：update(1,1,n,l,r,6)
  • 添加新元素到末尾： update(1,1,n,cnt,cnt,6)，使用cnt记录元素的个数，cnt=n+1…则两个区间表示同一个值，意味着增加一个新的叶子节点

懒惰修改（查询）问题

前面我们的线段树只适用于区间的求极值问题，给你一个区间，求出这个区间的极大值或极小值。

但是如果需要做整个区间的修改问题该怎么办呢 ？

这就需要用到我们前面的update函数，前面的update函数只能用于修改一个节点（因为如果修改一个区间的话，上面的update函数会出错），因此如果要修改整个区间的值，每个节点加上d值，如果使用我们最简单的update函数的话，修改m个点只能是一个一个节点最简单的修改，则需要O（mnlongn）这显然是低效的，因此我们使用懒惰标记技术。

这项技术使得对整个区间的修改m次也能降低到O（mlogn）

线段树的节点tree[i]记录了这个区间的值，可以再定义一个tag[i]用来统一记录i这个区间的修改，而不是一个一个节点的修改，这个办法就叫做懒惰标记

当修改的是一个线段区间时，就只对这个线段区间做整体上的修改，其内部的每个孩子节点都不做修改，只有当线段区间的一致性被破坏时，才把变化值传递给其孩子节点。

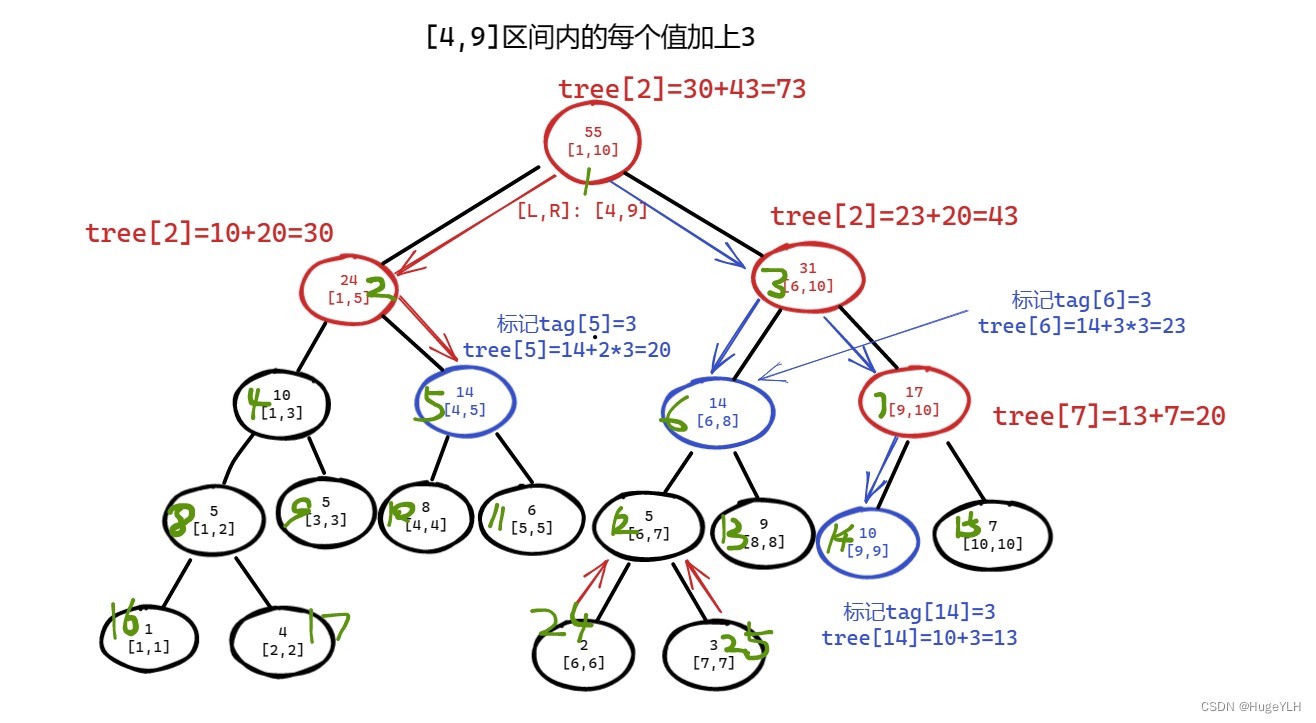
修改区间的update函数的实现如图所示：

  • 蓝色代表首先递归到的线段节点
  • 红色代表由蓝色节点的修改引起的push_up修改
  • 每个节点的绿色数字代表节点编号，一个数字表示节点的区间和，[x,x]表示这个区间
    在这里插入图片描述

对区间[4,9]的每个值加上3的操作详解：

  1. 首先左子树递归到 [4,5]这个区间（如果你还不知道怎么递归，则看上面的区间最大值的线段树的解释），这个线段区间编号为5，表示tag[5]=3，由于其有两个孩子节点，所以更新tree[5]=14 + 2*3 = 20
  2. 左子树递归返回，修改线段区间为编号2的节点，更新其值为两个孩子的和，tree[2]=tree[4]+tree[5]=10+20=30
  3. 返回，进入右子树递归，到达 6节点[6,8]区间，标记tag[6]=3，更新tree[6]的值。
  4. 返回，进入右子树的左子树，到达 14节点[9,9]区间，标记tag[14]=3，更新tree[14]返回，更新tree[7]=tree[14]+tree[15]=20，再次返回，更新tree[3]=tree[6]+tree[7]=43，最后递归返回更新tree[1]

我们修改区间的过程就是这样的，但是如果出现了两次更新同一个区间该怎么办？？

例如第一次更新[4,9]，第二次更新[5,8]，但是他们都会影响到编号为5的节点 [5，5]，第一次修改时标记tag[5]，然后第二次修改也会进行到11节点 [5,5]的修改，进而破坏了tag[5]的标记，此时原tag[5]记录的统一区间修改就只能往它的孩子节点传递，然后把tag[5]清零

总结的说：对于多个重复区间的修改，我们使用一个push_down函数来解决区间修改的冲突问题。

  • 首先检查p节点的tag[p]看看有没有标记，如果有则说明是之前某次修改过的区间，则需要将tag[p]下移到孩子节点，然后把原始tag[p]清零

tag标记设计

int tag[N << 2];
void addtag(ll i, ll pl, ll pr, ll d)
{
	tag[i] += d;	//此节点加上tag
	tree[i] += (pr - pl + 1) * d;	//更新tree
}

push_down 函数

inline void push_down(int i,int pl,int pr)
{
	if (tag[i])
	{	//如果被标记过
		int mid=(pl+pr)>>1;
		//下移标记
		addtag(ls(i),pl,mid);//左孩子
		addtag(rs(i),mid+1,pr);//右孩子
		tag[i]=0;//原始标记清零
	}
}

改进的更新函数

void update(int i, int pl, int pr, int L, int R, int d)
{
	if (L <= pl && pr <= R)
	{
		addtag(i, pl, pr, d);	//给节点打上标记，等到下一次区间修改到i这个节点时会用到
		return;
	}
	push_down(i, pl, pr);	//如果不能覆盖，递归到每一个节点时，检查是否有没有被标记过，把tag传递给子树
	int mid = (pl + pr) >> 1;
	if (L <= mid) update(ls(i), pl, mid, L, R, d);
	if (R > mid) update(rs(i), mid + 1, pr, L, R, d);
	push_up(i);
}

查询函数：注意查询的时候也会使用push_down

int query(int i, int pl, int pr, int L, int R)
{
	int res = 0;
	if (L <= pl && pr <= R)
	{
		return tree[i];	//完全覆盖，直接返回
	}
	push_down(i, pl, pr);	//不能覆盖，递归子树
	int mid = (pl + pr) >> 1;
	if (L <= mid) res +=  query(ls(i), pl, mid, L, R);			//区间求和
	if (R > mid) res +=  query(rs(i), mid + 1, pr, L, R);		//区间求和
	return res;
}

关于本节的全部源代码

//线段树：区间最大值
namespace test45
{
	const int N = 5e+5;
	int n, q;
	const int inf = 0x3f3f3f3f;
	int nums[N], tree[N];
	inline int ls(int i)//左孩子
	{
		return i << 1;
	}
	inline int rs(int i)//右孩子
	{
		return i << 1 | 1;
	}
	inline void push_up(int i)
	{
		tree[i] = max(tree[ls(i)], tree[rs(i)]);
	}
	void build(int i, int pl, int pr)
	{
		if (pl == pr)
		{
			tree[i] = nums[pl];
			return;
		}
		int mid = (pl + pr) >> 1;
		build(ls(i), pl, mid);
		build(rs(i), mid + 1, pr);
		push_up(i);	//自底向上传递区间值
	}
	void update(int i, int pl, int pr, int L, int R, int d)
	{
		if (L <= pl && pr <= R)
		{
			tree[i] = d;
			return;
		}
		int mid = (pl + pr) >> 1;
		if (L <= mid) update(ls(i), pl, mid, L, R, d);
		if (R > mid) update(rs(i), mid + 1, pr, L, R, d);
		push_up(i);
	}
	int query(int i, int pl, int pr, int L, int R)
	{
		int res = -inf;
		if (L <= pl && pr <= R)
		{
			return tree[i];
		}
		int mid = (pl + pr) >> 1;
		if (L <= mid) res = max(res, query(ls(i), pl, mid, L, R));
		if (R > mid) res=max(res,query(rs(i), mid + 1, pr, L, R));
		return res;
	}
	void test()
	{
		cin >> n >> q;
		int cnt = 0;
		for (int i = 1; i <= n; i++)
		{
			cin >> nums[i];
		}
		build(1, 1, n);
		for (int i = 1; i <= q; i++)
		{
			int l, r;
			cin >> l >> r;
			cnt = n + 1;
			update(1, 1, n + 1, n + 1, n + 1,99);
			//cout << query(1, 1, n, l, r) << endl;
		}
	}
}

//线段树：懒惰标记，区间修改查询
namespace test46
{
	const int N = 5e+5;
	int n, q;
	const int inf = 0x3f3f3f3f;
	int nums[N], tree[N << 2];
	int tag[N << 2];
	void addtag(ll i, ll pl, ll pr, ll d)
	{
		tag[i] += d;	//此节点加上tag
		tree[i] += (pr - pl + 1) * d;	//更新tree
	}
	inline int ls(int i)//左孩子
	{
		return i << 1;
	}
	inline int rs(int i)//右孩子
	{
		return i << 1 | 1;
	}
	inline void push_up(int i)
	{
		tree[i] = tree[ls(i)]+ tree[rs(i)];	//求区间和
	}
	inline void push_down(int i,int pl,int pr)
	{
		if (tag[i])
		{
			//如果被标记过，下移标记
			int mid = (pl + pr) >> 1;
			addtag(ls(i), pl, mid, tag[i]);
			addtag(rs(i), mid + 1, pr, tag[i]);
			tag[i] = 0;	
		}
	}
	void build(int i, int pl, int pr)
	{
		tag[i] = 0;	//懒惰标记赋值为0
		if (pl == pr)
		{
			tree[i] = nums[pl];	//叶子节点赋值
			return;
		}
		int mid = (pl + pr) >> 1;	//分治
		build(ls(i), pl, mid);
		build(rs(i), mid + 1, pr);
		push_up(i);	//自底向上传递区间值
	}
	void update(int i, int pl, int pr, int L, int R, int d)
	{
		if (L <= pl && pr <= R)
		{
			addtag(i, pl, pr, d);	//给节点打上标记，等到下一次区间修改到i这个节点时会用到
			return;
		}
		push_down(i, pl, pr);	//如果不能覆盖，递归到每一个节点时，检查是否有没有被标记过，把tag传递给子树
		int mid = (pl + pr) >> 1;
		if (L <= mid) update(ls(i), pl, mid, L, R, d);
		if (R > mid) update(rs(i), mid + 1, pr, L, R, d);
		push_up(i);
	}
	int query(int i, int pl, int pr, int L, int R)
	{
		int res = 0;
		if (L <= pl && pr <= R)
		{
			return tree[i];	//完全覆盖，直接返回
		}
		push_down(i, pl, pr);	//不能覆盖，递归子树
		int mid = (pl + pr) >> 1;
		if (L <= mid) res +=  query(ls(i), pl, mid, L, R);		//区间求和
		if (R > mid) res +=  query(rs(i), mid + 1, pr, L, R);		//区间求和
		return res;
	}
	void test()
	{
		cin >> n >> q;
		int cnt = 0;
		for (int i = 1; i <= n; i++)
		{
			cin >> nums[i];
		}
		build(1, 1, n);
		for (int i = 1; i <= q; i++)
		{
			int q, l, r, d;
			cin >> q;
			if (q == 1)
			{
				cin >> l >> r >> d;
				update(1, 1, n, l, r, d);
			}
			else
			{
				cin >> l >> r;
				cout << query(1, 1, n, l, r);
			}
		}
	}
}
int main()
{
	using namespace test46;
	test46::test();
	return 0;
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
心跳检测机制
Kafka-服务端-网络层-源码流程
200行代码实现N子棋(以五子棋为例)
24位真彩色转换为８位灰度图片（完整代码）
(void)0和0的区别及用法
Spring Cloud Alibaba 快速学习之 RocketMQ
最短路径 Dijkstra算法的Matlab代码实现
看你就懂，超详细java中的ClassLoader详解
小白云盘TV_v1.7.2.1 无限制网盘电视版
springboot医疗挂号管理系统
;