✅作者简介：嵌入式入坑者，与大家一起加油，希望文章能够帮助各位！！！！
📃个人主页：

一.栈的定义和特点

栈（stack）是一个特殊的线性表是限定仅在一端(通常在表尾进行插入，删除的线性表)，又称为后进先出（last in first out）的线性表简称 LIFO结构

栈是仅在表尾插入，删除操作的线性表，其实栈就是线性表的一个子集，表尾(an端)称为栈顶TOP，表头（a1端）称为栈底BASE.

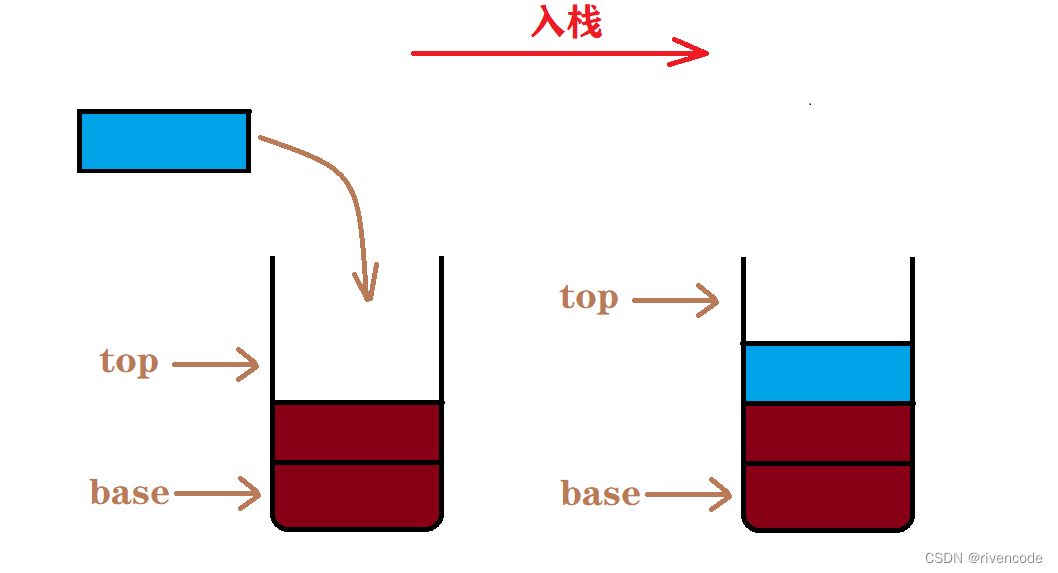
• 插入元素到栈顶的操作称为入栈、压栈、进栈

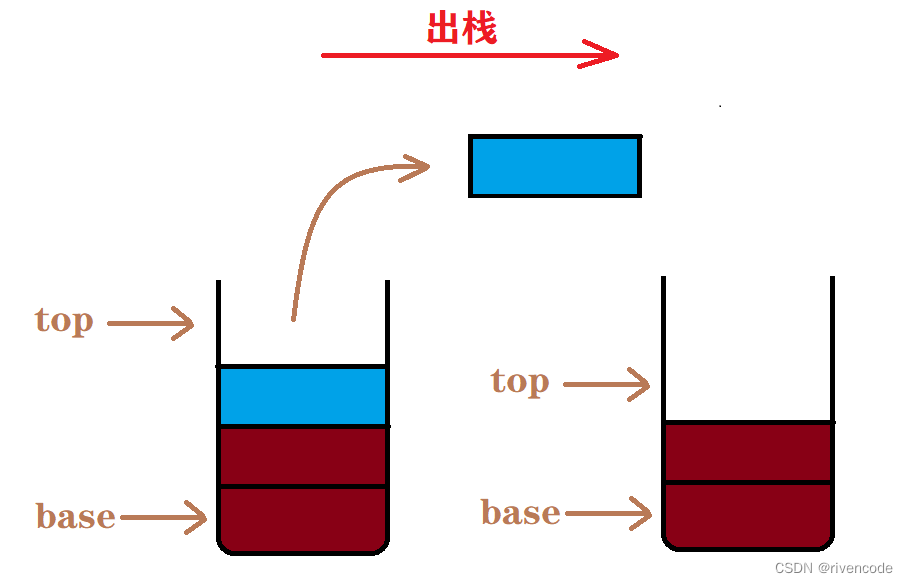
• 从栈顶删除元素的操作称为出栈
  
  栈的操作特性：后进先出

二.顺序栈与链栈的实现

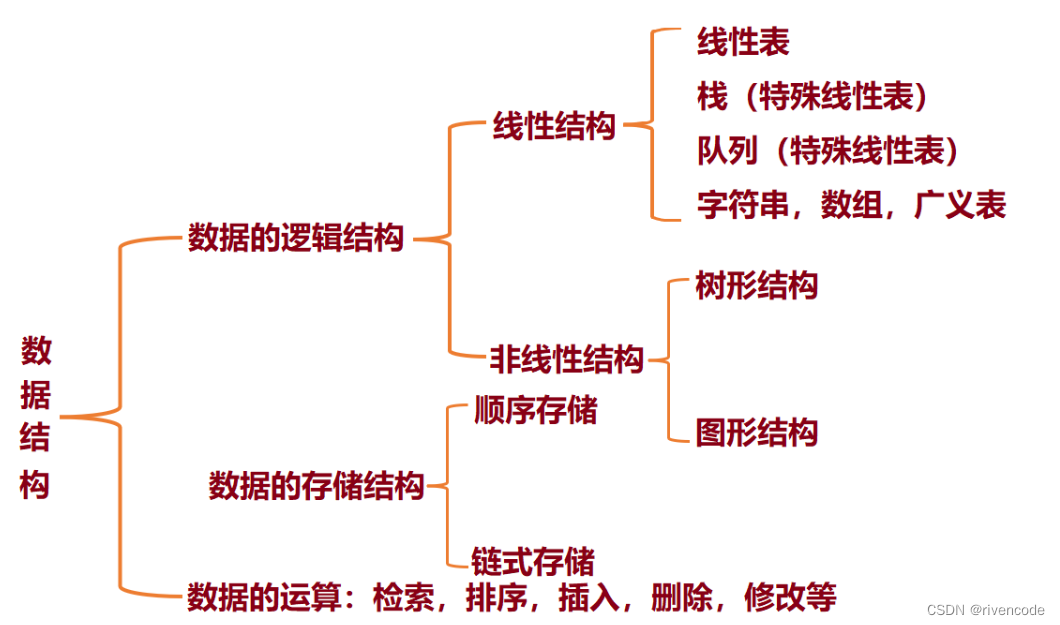
由于栈本身就是线性表，所以栈也有顺序存储与链式存储
栈的顺序存储：顺序栈
栈的链式存储：链式栈

1.顺序栈的实现

• 栈的顺序存储
  利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素，栈底在底地址端。

在C语言中一般用数组来实现栈的顺序存储：

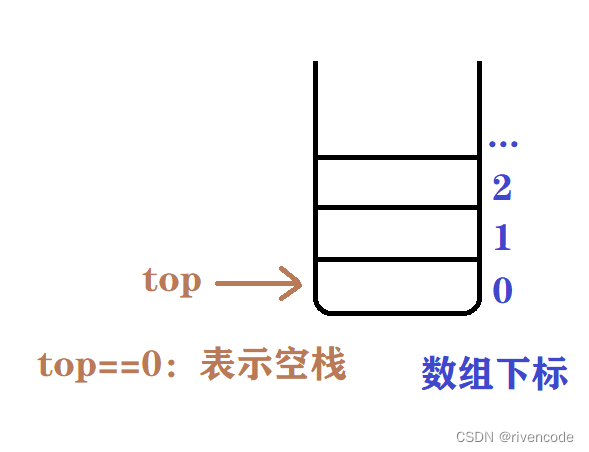
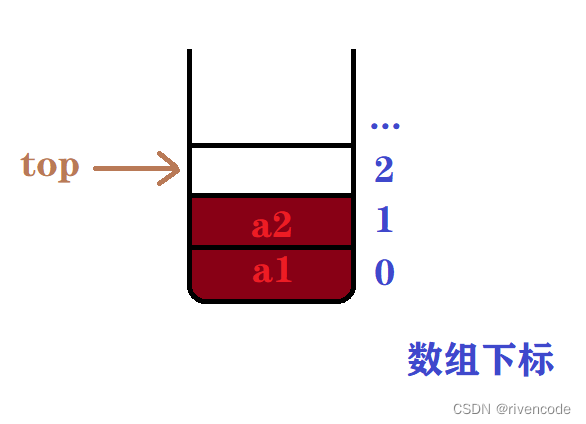
• 当栈为空时
  
• 当栈不为空时
  

为了操作更加方便top一般存储栈顶元素上面一个元素的下标

只要理解上面那句话，然后其实就是顺序表的尾插与尾删，用尾做了栈顶。因为顺序栈实现比较简单，这里直接上代码

stack.h

```c
#ifndef   __QSTACK_H
#define  __QSTACK_H

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>
#include <malloc.h>

typedef    int   STDataType;

typedef struct  Stack
{
	STDataType * a;
	int top;
	int capacity;
}ST;

//初始化
void  StackInit(ST* ps);
//销毁
void  StackDestory(ST* ps);
//入栈
void  StackPush(ST*ps, STDataType x);
//出栈
void  StackPop(ST*ps);
//取栈顶元素
STDataType  StackTop(ST*ps);
//栈元素个数
int    StackSize(ST*ps);
//判断栈是否为空
bool  StackEmpty(ST*ps);
#endif /* __QSTACK_H */

stack.c

#include "Stack.h"
//初始化
void  StackInit(ST* ps)
{
	assert(ps !=NULL);
	ps->a = (STDataType*)malloc(sizeof(STDataType) * 10);
	if (ps->a == NULL)
	{
		printf("扩容失败\n");
		exit(-1);
	}
	ps->capacity = 10;
	ps->top = 0;
}
//销毁
void  StackDestory(ST* ps)
{
	assert(ps != NULL);
	free(ps->a);
	ps->capacity = 0;
	ps->top = 0;
}
//入栈
void  StackPush(ST*ps, STDataType x)
{
	assert(ps != NULL);
	//容量不够增容
	if (ps->top == ps->capacity)
	{
		STDataType *tmp = (STDataType *)realloc(ps->a, ps->capacity * 2 * sizeof(STDataType));
		if (tmp == NULL)
		{
			printf("扩容失败\n");
			exit(-1);
		}
		else
		{
			ps->a = tmp;
			ps->capacity *= 2;
		}
	}
	ps->a[ps->top] = x;
	ps->top++;
}
//出栈
void  StackPop(ST*ps)
{
	assert(ps != NULL);
	assert(ps->top> 0);
	ps->top--;
}

STDataType  StackTop(ST*ps)
{
	assert(ps != NULL);
	assert(ps->top> 0);
	return ps->a[ps->top - 1];
}
//栈元素个数
int  StackSize(ST*ps)
{
	return ps->top;
}
//判断栈是否为空
bool  StackEmpty(ST*ps)
{
	return ps->top == 0;
}

2.链式栈的实现

1.如果用尾结点做栈顶，那么要用双向链表，因为你用单向链表话出栈，需要找尾结点以及尾结点前一个结点，时间复杂度为O（n），时间效率低。

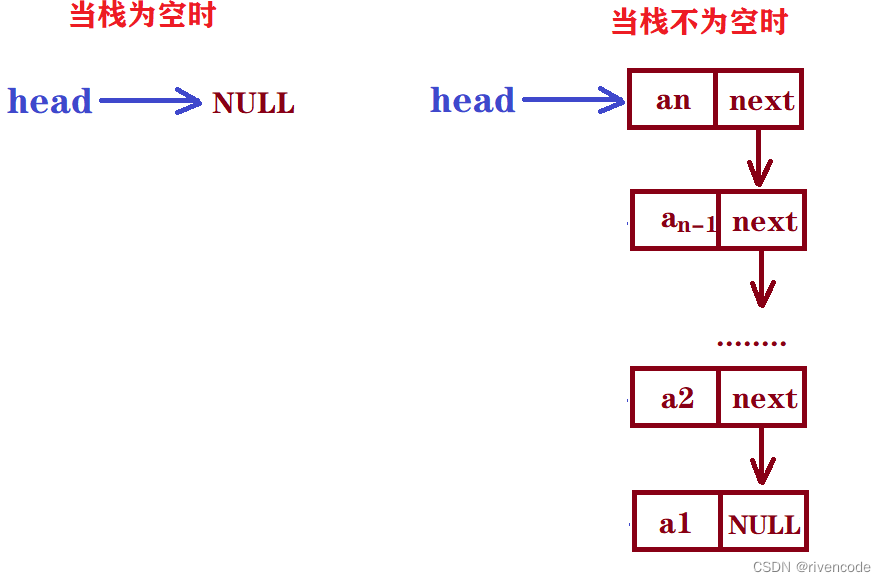
2.如果使用单链表实现，那么就用头结点做栈顶，入栈出栈，其实就是单链表的头插与头删。

直接上代码：
stack.h

#ifndef    __STACK_H
#define   __STACK_H

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>
#include <malloc.h>
typedef    int   STDataType;

typedef struct  StackNode
{
	STDataType data;
	struct  Stack *next;
}SNode;

typedef struct  Stack
{
	SNode *head;
}ST;

//初始化
void  StackInit(ST* ps);
//销毁
void  StackDestory(ST* ps);
//入栈
void  StackPush(ST*ps, STDataType x);
//出栈
void  StackPop(ST*ps);
//取栈顶元素
STDataType  StackTop(ST*ps);
//栈中元素个数
int    StackSize(ST*ps);
//判断栈是否为空
bool  StackEmpty(ST*ps);

#endif /* __STACK_H */

stack.c

#include "stack.h"

void  StackInit(ST* ps)
{
	assert(ps != NULL);
	ps->head = NULL;
}
void  StackDestory(ST* ps)
{
	assert(ps != NULL);
	SNode*cur = ps->head;
	while (cur)
	{
		SNode*next = cur->next;
		free(cur);
		cur = next;
	}
	ps->head = NULL;
}

void  StackPush(ST*ps, STDataType x)
{
	assert(ps != NULL);
	//创建新结点
	SNode* NewNode = (SNode*)malloc(sizeof(SNode));
	if (NewNode == NULL)
	{
		printf("malloc fail");
		exit(-1);
	}
	NewNode->data = x;
	NewNode->next = NULL;

	NewNode->next = ps->head;
	ps->head = NewNode;
}
void  StackPop(ST*ps)
{
	assert(ps != NULL);
	//栈不能为空
	assert(ps->head != NULL);
	SNode*next = ps->head->next;
	free(ps->head);
	ps->head = next;
}
STDataType StackTop(ST*ps)
{
	assert(ps != NULL);
	//栈不能为空
	assert(ps->head != NULL);
	return ps->head->data;
}

int  StackSize(ST*ps)
{
	assert(ps != NULL);
	int count = 0;
	SNode*cur = ps->head;
	while (cur)
	{
		count++;
		cur = cur->next;
	}
	return count;
}
bool  StackEmpty(ST*ps)
{
	return ps->head == NULL;
}

3.顺序栈与链栈的对比

推荐使用顺序栈：

1.在开辟内存的角度来说，链栈插入元素就需要开辟一个结点的内存，而顺序栈，是隔多个结点在整体分配一块内存。相比之下链栈需要频繁申请空间。

2.CPU向内存取数据的时候是一次取地址连续的空间里的数据，在CPU中的高速缓存或寄存器，如果是顺序栈，取数据的命中率将大大增加，而由于链栈的结点物理存储并不是连续的也就是说结点的地址各不相同，则CPU在取数据的时候每次都要向内存中去取，相比之下效率较低。

当然算法都是灵活多变的，怎么实现取决于场景和你自己

三.队列的定义和特点

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出，FIFO(First In First Out)
入队列：进行插入操作的一端称为队尾（表尾）
出队列：进行删除操作的一端称为队头（表头）

队列的操作特性：先进先出

四.顺序队与链队的实现

由于队列本身就是线性表，所以队列也有顺序存储与链式存储
队列的顺序存储：顺序栈（一般是循环队列）
队列链式存储：链式栈

1.顺序队列(循环)的实现

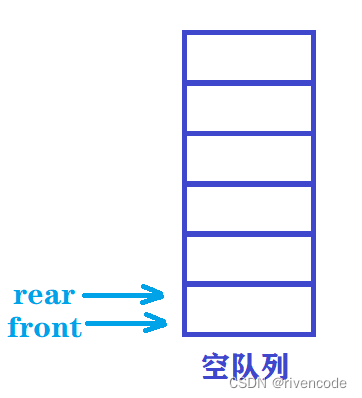
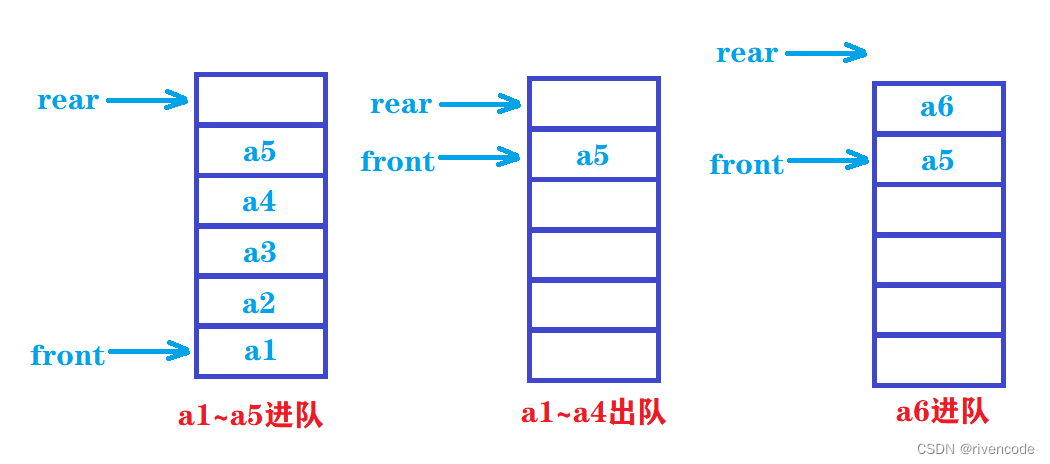
顺序队列：在内存中用一组地址连续存储单元依次存放从对头到队尾的数据元素，同时设置两个指针front和rear分别指示队头元素和队尾元素的位置

当队列为空时front == rear

队列不为空

rear指示的队尾元素的下一个位置

如果是像上面一样不使用循环队列会有很大的缺陷
由于队列是先进先出：只能从表尾插入元素从表头删除元素

则删除一个元素则该元素的空间就无法再进行利用，数组的前端可能会出现很多空的单元，这种现象称为假溢出，则空间利用率太低。

如果我们要采用顺序存储来实现队列只能使用循环队列

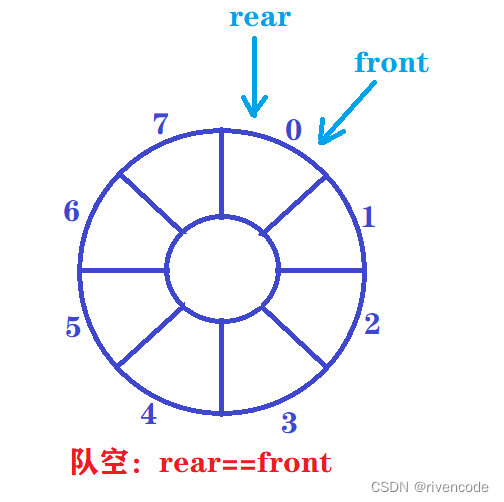
定义一个队列：

队空时

队非空

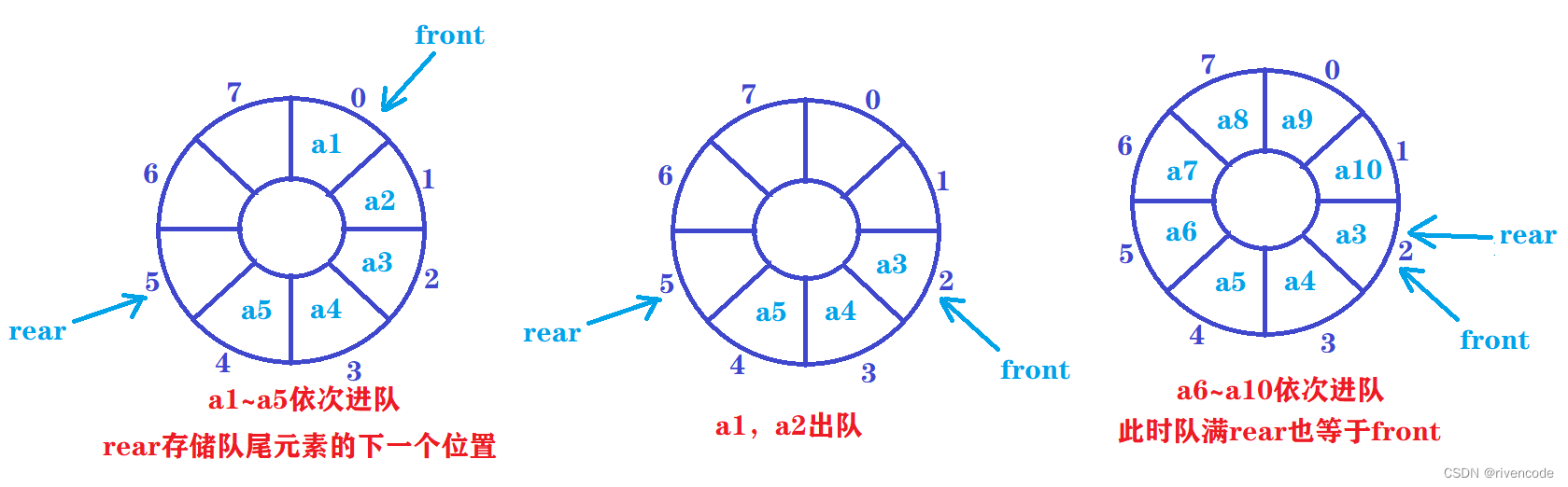
现在出现了两个问题：
1.队空与对满的条件都是rear==front
2.如果rear或者front指示了下标为7的位置，此时在进队一个元素rear如何指示下标为0的位置，或者此时在出队一个元素frontr如何指示下标为0的位置，进而实现循环。

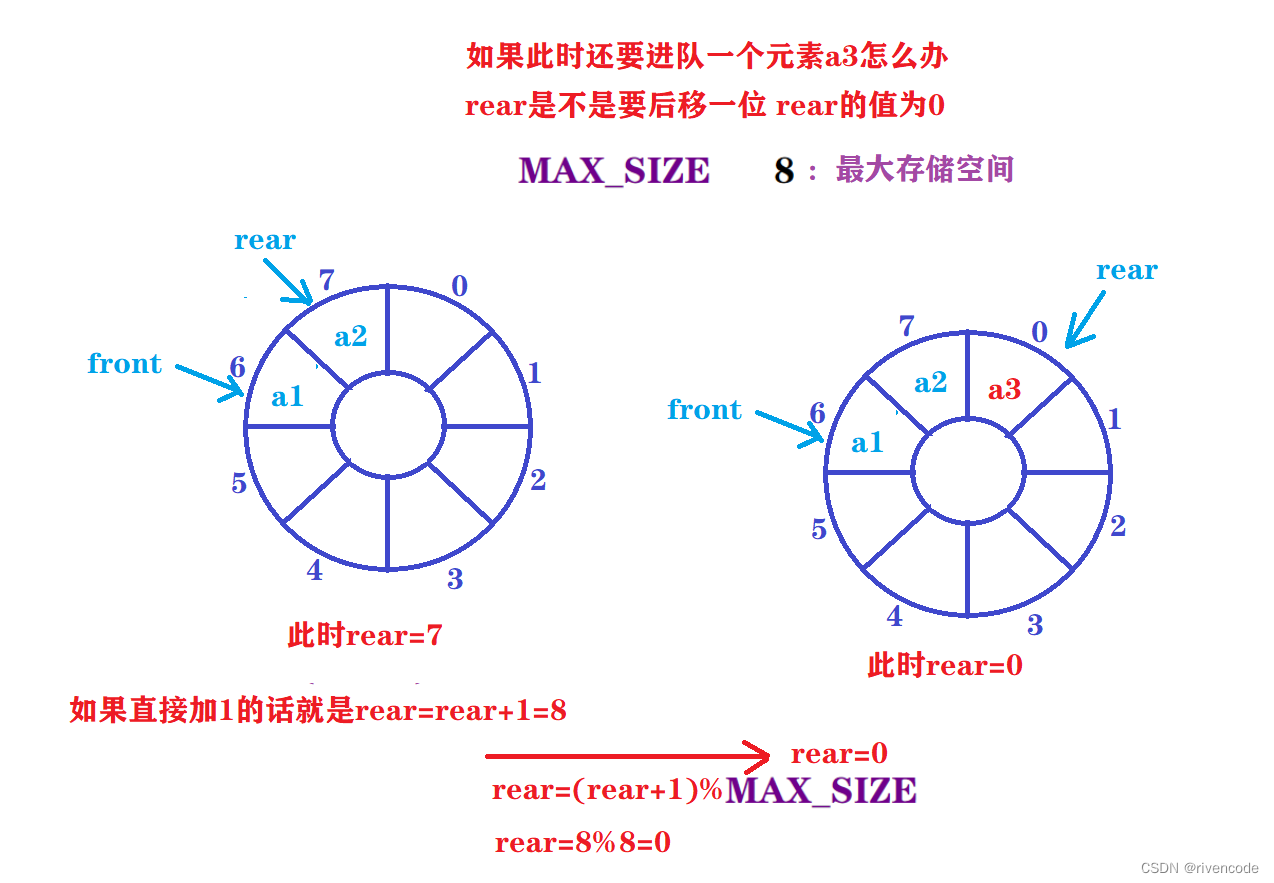
• 第一个问题如何实现循环：

front与rear一样
这里的MAX_SIZE是数组的最大容量
指针front 与rear在到达末尾后自动回到数组的起始位置，达到循环的目的

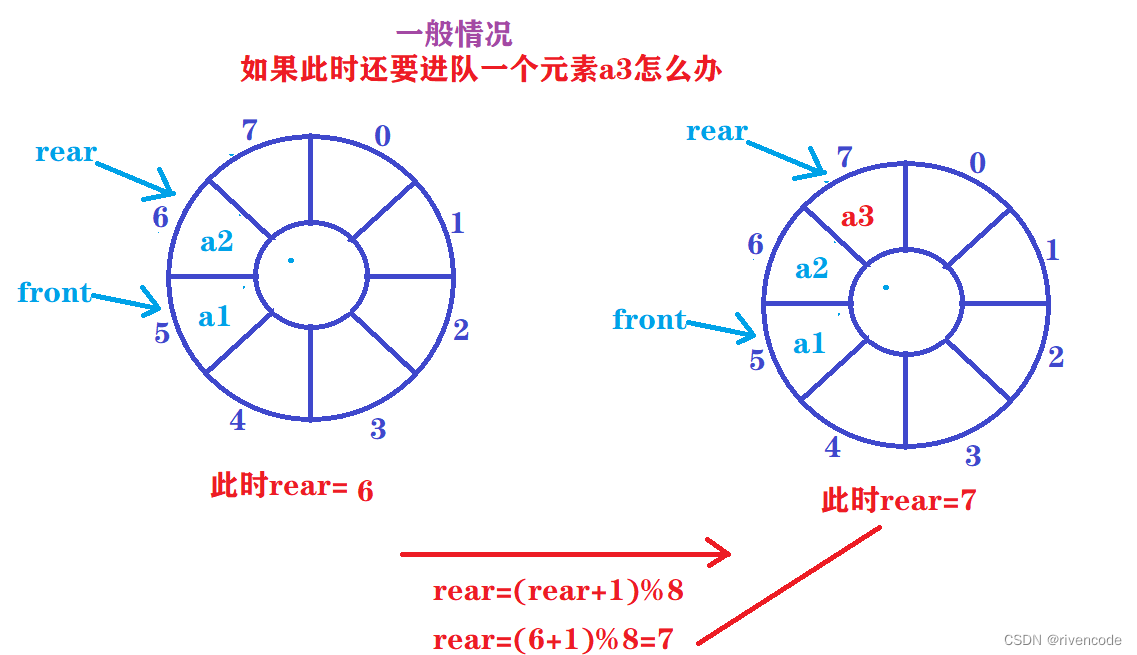
进队操作时：rear=(rear+1)%MAX_SIZE

出队操作时：front=(front+1)%MAX_SIZE

• 如何区分队空与对满的条件
  这里有三种解决方式：
  1.另外设一个标志以区别队空，队满。
  2.另设一个变量记录元素个数
  3.少用一个元素的空间

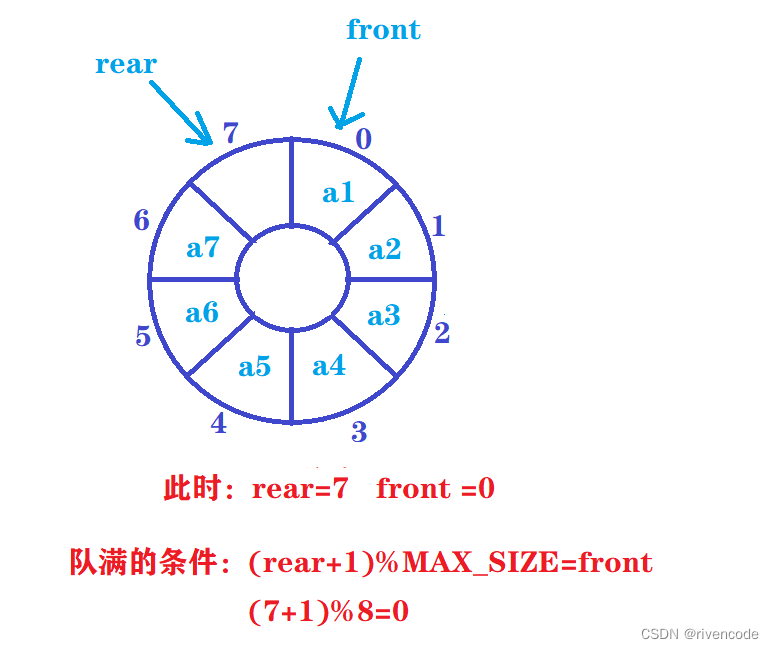
这里我们使用第三种方式非常方便：

循环队列满的条件：(rear+1)%MAX_SIZE = front

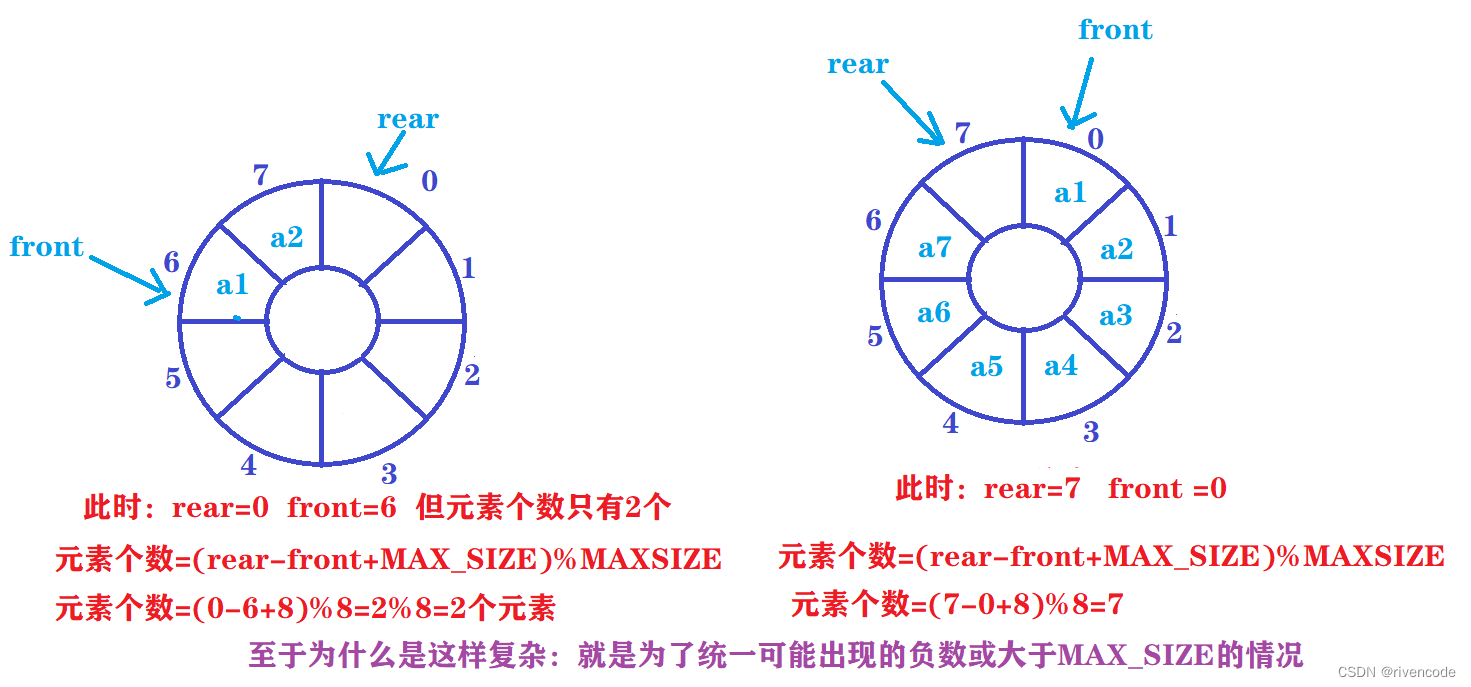
• 第三个问题如何求队列中元素个数
  
  队列中元素个数：(rear-front+MAX_SIZE)%MAX_SIZE
  别问公式怎么来的反正一切都是巧合，公式正好适用所有情况

现在已经解决了最重要的三个问题现在再去写循环队列就跟玩一样
首先循环队列只能是静态的，容量是固定的
循环队列空的条件：rear= front

进队操作时：rear=(rear+1)%MAX_SIZE

出队操作时：front=(front+1)%MAX_SIZE

循环队列满的条件：(rear+1)%MAX_SIZE = front

直接上代码了：

queue.h

#ifndef  __QUEUE_H
#define  __QUEUE_H

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

#define   MAX_SIZE      8
typedef  int	  QDataType;
typedef struct Queue
{
	QDataType data[MAX_SIZE];
	int front;
	int rear;
}Queue;


//初始化
void QueueInit(Queue * pq);
//进队
void QueuePush(Queue * pq, QDataType x);
//出队
void QueuePop(Queue * pq);
//取队头数据
QDataType QueueFront(Queue * pq);
QDataType QueueBack(Queue * pq);

int QueueSize(Queue * pq);
bool QueueEmpty(Queue * pq);
#endif /*__QUEUE_H*/

queue.c

#include "Queue.h"

//初始化
void QueueInit(Queue * pq)
{
	assert(pq!=NULL);
	pq->front = pq->rear = 0;
}

//进队
void QueuePush(Queue * pq, QDataType x)
{
	assert(pq != NULL);
	//队满进队失败
	if ((pq->rear + 1) % MAX_SIZE == pq->front)
	{
		printf("queue full");
		exit(-1);
	}
	pq->data[pq->rear] = x;
	pq->rear = (pq->rear + 1) % MAX_SIZE;
}

//出队
void QueuePop(Queue * pq)
{
	assert(pq != NULL);
	//队空
	assert(pq->front != pq->rear);
	pq->front = (pq->front + 1) % MAX_SIZE;

}

//取队头数据
QDataType QueueFront(Queue * pq)
{
	assert(pq != NULL);
	//队空
	assert(pq->front != pq->rear);
	return pq->data[pq->front];
}

int QueueSize(Queue * pq)
{
	assert(pq != NULL);
	return  ((pq->rear) - (pq->rear) + MAX_SIZE) % MAX_SIZE;
}

bool QueueEmpty(Queue * pq)
{
	assert(pq != NULL);
	return pq->front == pq->rear;
}

2.链队列的实现

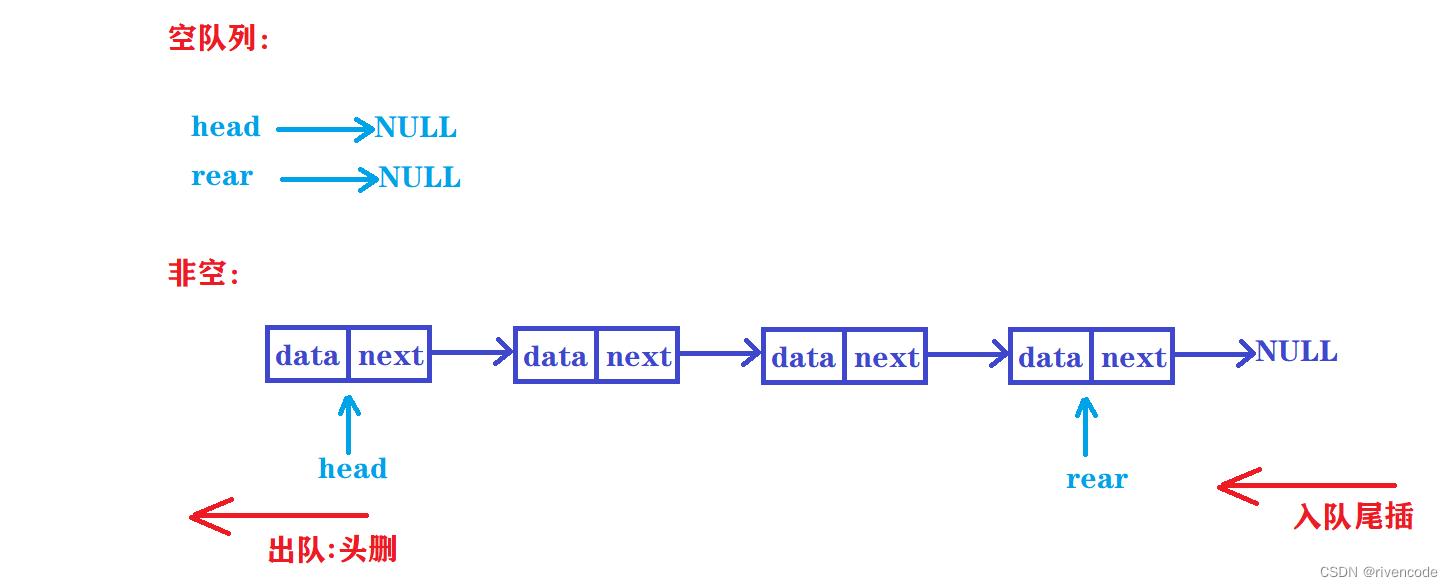
采用链表形式的队列称为链队列，队列中每一个元素对应的链表中的一个结点，并设两个分别指示队头和队尾的指针。

其实本质：
出队：链表的头删
入队：链表的尾插

直接上代码：

queue.h

#ifndef  __QUEUE_H
#define  __QUEUE_H

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>
#include <malloc.h>

typedef  int	  QDataType;


typedef struct QueueNode
{
	 struct QueueNode *next;
	 QDataType data;
}QNode;

typedef struct Queue
{
	 QNode*head;
	 QNode*tail;
}Queue;

//初始化
void QueueInit(Queue * pq);
//销毁
void QueueDestory(Queue * pq);
//进队
void QueuePush(Queue * pq, QDataType x);
//出队
void QueuePop(Queue * pq);
//取队头数据
QDataType QueueFront(Queue * pq);
QDataType QueueBack(Queue * pq);

int QueueSize(Queue * pq);
bool QueueEmpty(Queue * pq);
#endif /*__QUEUE_H*/

queue.c

#include "Queue.h"


void QueueInit(Queue * pq)
{
	assert(pq !=NULL);
	pq->head = pq->tail = NULL;
}

void QueueDestory(Queue * pq)
{
	assert(pq != NULL);
	QNode * cur = pq->head;
	while (cur)
	{
		QNode * next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;
}

void QueuePush(Queue * pq, QDataType x)
{
	assert(pq != NULL);
	QNode * NewNode = (QNode *)malloc(sizeof(QNode));
	if (NewNode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	NewNode->data = x;
	NewNode->next = NULL;
	//空队列
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = NewNode;
	}
	//队列不为空
	else
	{
		pq->tail->next = NewNode;
		pq->tail = NewNode;
	}

	
}
void QueuePop(Queue * pq)
{
	assert(pq != NULL);
	assert(pq->head !=NULL);
	//只有一个结点,保证tail指针也置NULL
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode *next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	 
}
QDataType QueueFront(Queue * pq)
{
	assert(pq != NULL);
	assert(pq->head != NULL);
	 return pq->head->data;
}
QDataType QueueBack(Queue * pq)
{
	assert(pq != NULL);
	assert(pq->head != NULL);
	return pq->tail->data;
}

int QueueSize(Queue * pq)
{
	assert(pq != NULL);
	int count = 0;
	QNode *cur = pq->head;
	while (cur)
	{
		cur = cur->next;
		count++;
	}
	return count;
}

bool QueueEmpty(Queue * pq)
{
	return  pq->head == NULL;
}

3.顺序队列与链队的对比

链式存储结构的优点：
空间利用率高需要一个空间就分配一个空间，一般没有队满的情况
顺序存储的优点：
存储密度为1最高，因为没有指针域空间利用率高
顺序存储的缺点：
容量固定，容易造成空间的浪费或者队满溢出的情况

如果能事先确定队列的长度，队长的变化不大，可以考虑使用顺序队列，反之采用链队列更加合适