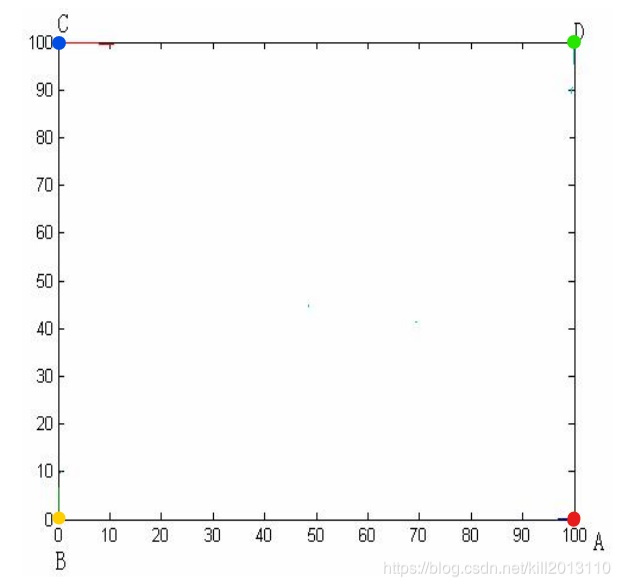
如图1,在正方形ABCD的四个顶点各有一个人。设在初始时刻t=0时，四人同时出发匀速以v沿顺时针走向下一个人。如果他们始终对准下一个人为目标行进，最终结果会如何。作出各自的运动轨迹。

• matlab模拟脚本的代码:

n=500;          %总时刻数
x=zeros(4,n);   %产生4行n列个零来放置坐标矩阵
y=zeros(4,n);
dt=0.02;        %时间间隔
v=10;           %速度
%四个人初始位置的横,纵坐标:
x(1,1)=100; y(1,1)=0;
x(2,1)=0;   y(2,1)=0;
x(3,1)=0;   y(3,1)=100;
x(4,1)=100; y(4,1)=100;

for j=1:n-1
    for i=1:3   %前三个人的位置更新:
        d=sqrt((x(i+1,j)-x(i,j))^2+(y(i+1,j)-y(i,j))^2);    %第i个人和第i+1个人之间j时刻的距离
        dircos=(x(i+1,j)-x(i,j))/d;   %第i个人j时刻运动方向的cos和sin值
        dirsin=(y(i+1,j)-y(i,j))/d;
        x(i,j+1)=x(i,j)+v*dt*dircos;    %第i个人j+1时刻的位置的横,纵坐标
        y(i,j+1)=y(i,j)+v*dt*dirsin;
    end
                %第四个人的位置更新:
    d=sqrt((x(1,j)-x(4,j))^2+(y(1,j)-y(4,j))^2);    %第4个人和第1个人之间j时刻的距离
    dircos=(x(1,j)-x(4,j))/d;   %第4个人j时刻运动方向的cos和sin值
    dirsin=(y(1,j)-y(4,j))/d;
    x(4,j+1)=x(4,j)+v*dt*dircos;    %第4个人j+1时刻的位置的横,纵坐标
    y(4,j+1)=y(4,j)+v*dt*dirsin;
    
                %给第j时刻四个人的位置作图:
    plot(x(1,j),y(1,j),'r*',x(2,j),y(2,j),'y*',x(3,j),y(3,j),'b*',x(4,j),y(4,j),'g*')
    hold on
    pause(0.001)  %暂停0.001秒
end

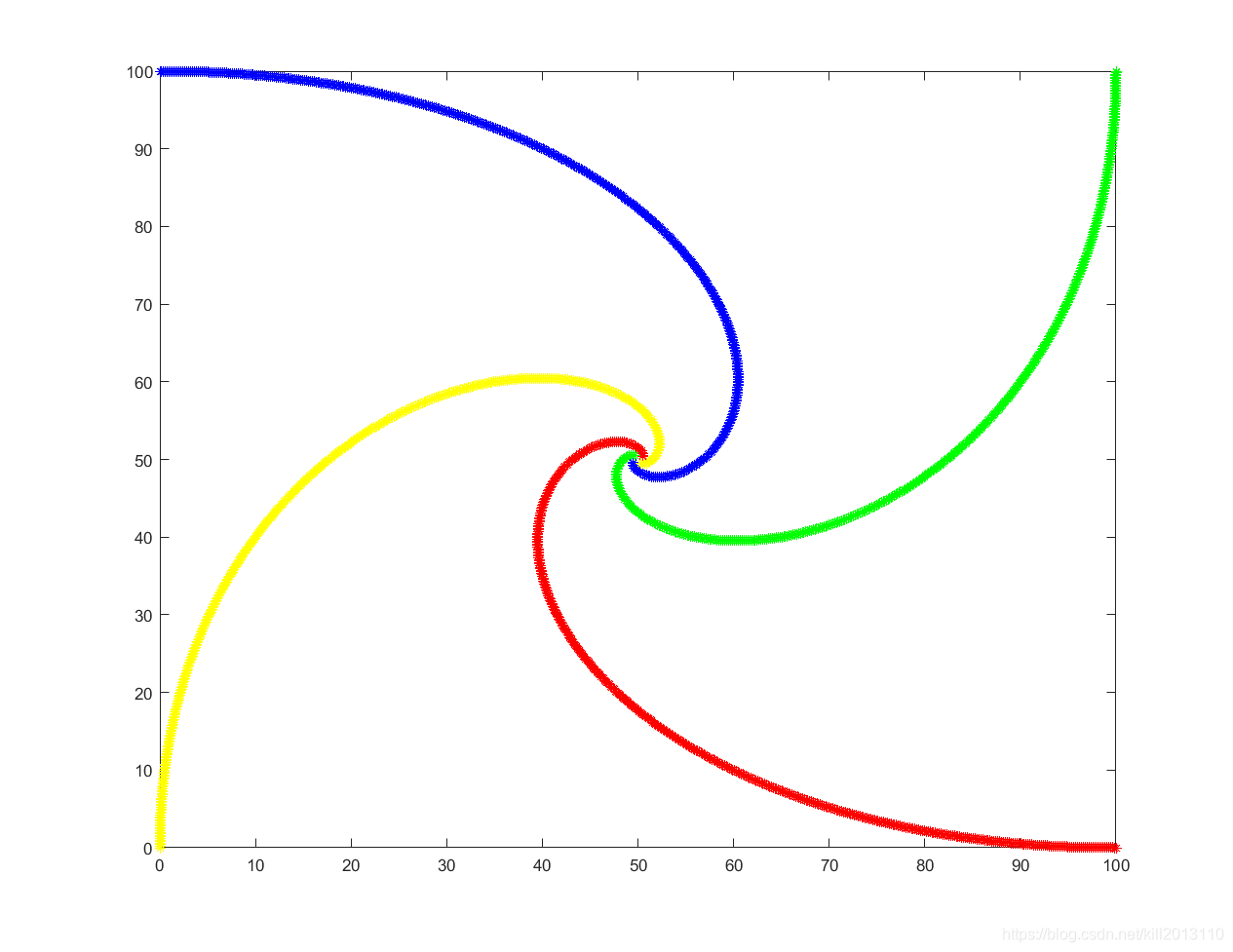
• 结果: