链接

我的代码：

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(!head||!head->next)return false;
        ListNode* last = head;
        ListNode*slow = head;
        while(last&&last->next){
            last = last->next->next;
            slow = slow->next;
            if(last==slow){
                return true;
            }
        }
        return false;
    }
};

另一种做法：

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(!head||!head->next)return false;
        unordered_set<ListNode*> visited;
        ListNode*cur = head;
        while(cur){
            if(visited.count(cur)){
                return true;
            }
            visited.insert(cur);
            cur = cur->next;
        }
        return false;
    }
};

 另一种做法：

class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(!head||!head->next)return false;
        ListNode*s = head,*f = head->next;
        while(f){
            s = s->next,f = f->next;
            if(!f){
                return false;
            }
            f = f->next;
            if(s==f){
                return true;
            }
        }
        return false;
    }
};

一和三都是快慢指针做法，它的时间复杂度是O(N)的。 

比如：链表没有环，那么快指针会遍历链表一遍，慢指针遍历一半，共3/2n，所以是O(N);

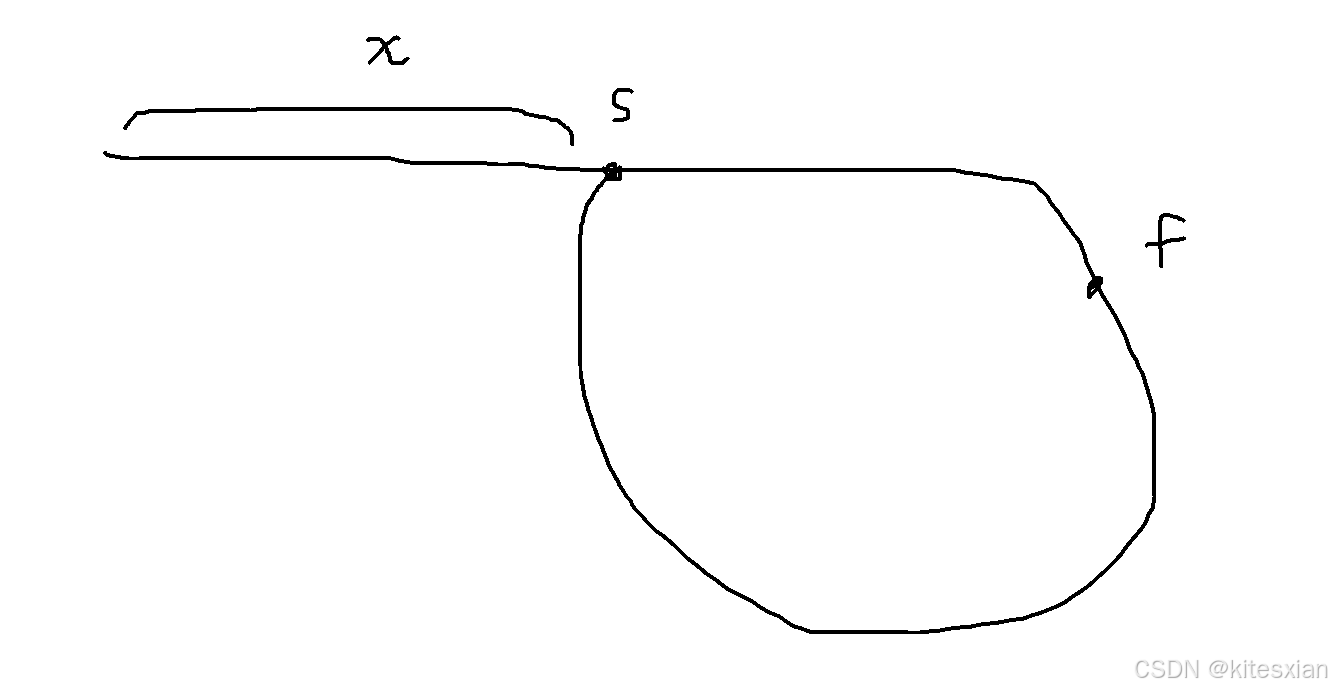
如果有环：

如上图，快指针走了2x步，慢指针走了x步，何时相遇呢？

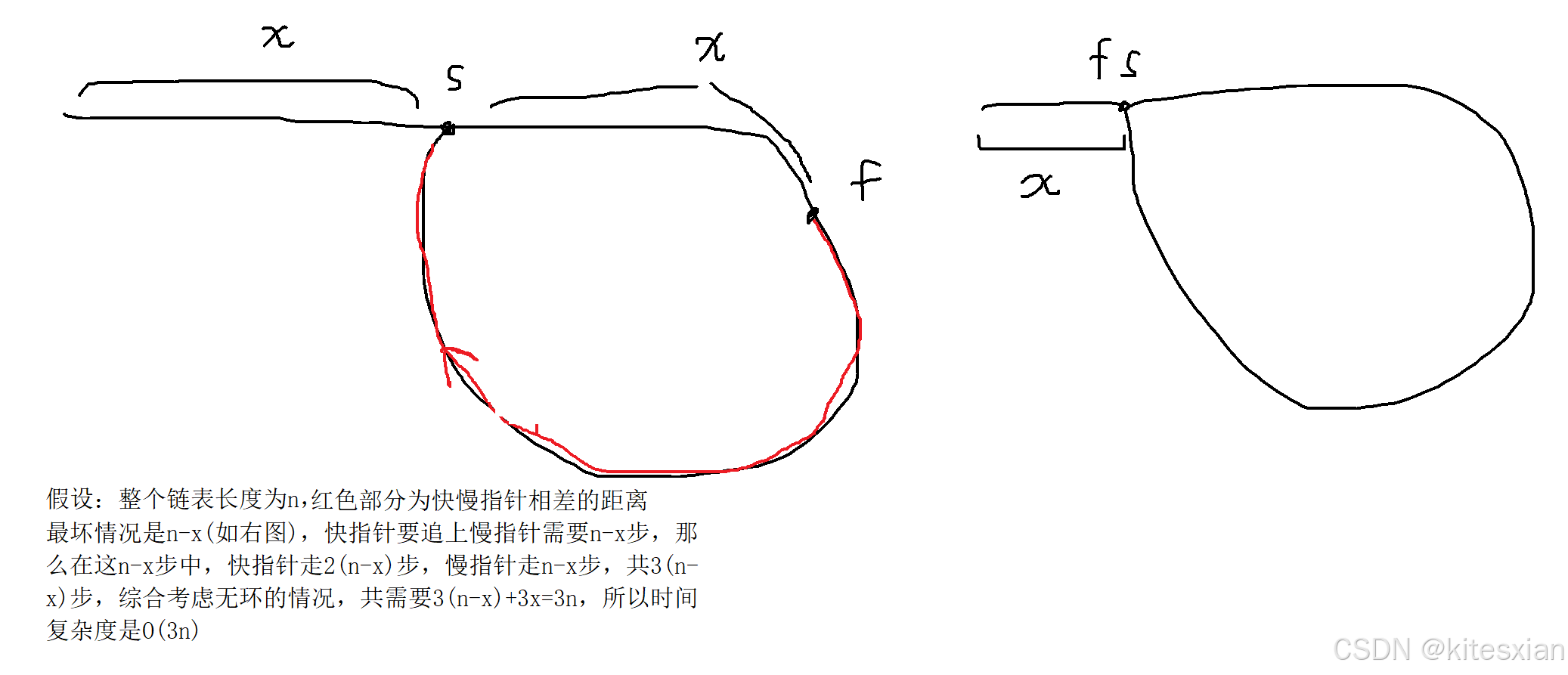
注：当慢指针走到环入口时，快指针可能在环内已经走了很多圈或者一圈，总之，快指针在环的某个位置，此时慢指针在入口处。然后快指针移动两步，慢指针移动一步， 相对速度为1，也就是说每循环一次，他们的距离减少1，那么如果它们距离为K的话，循环K次，它们就会相遇。