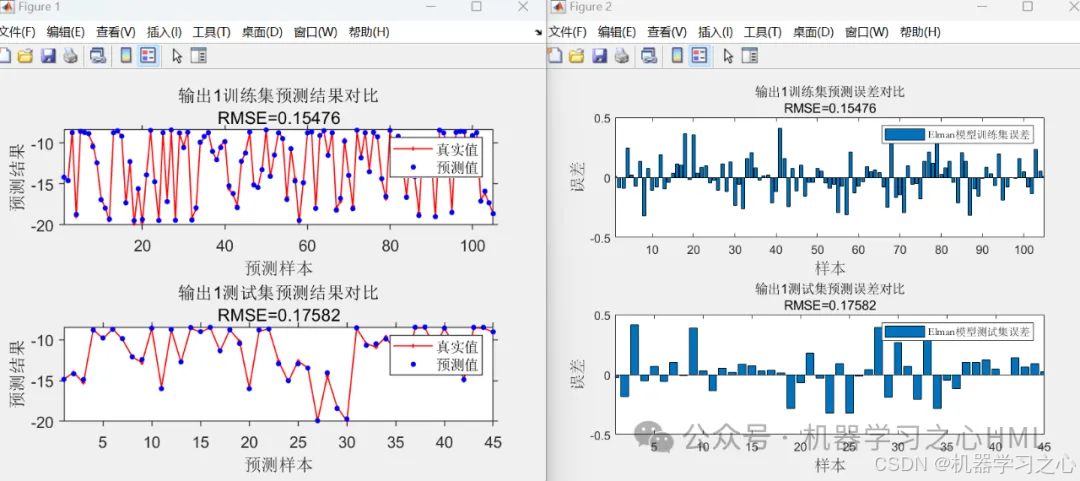
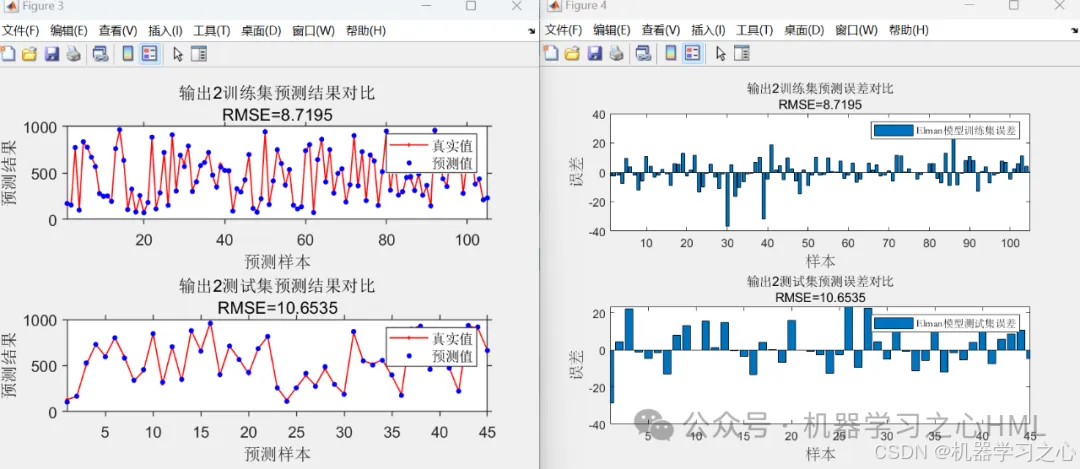
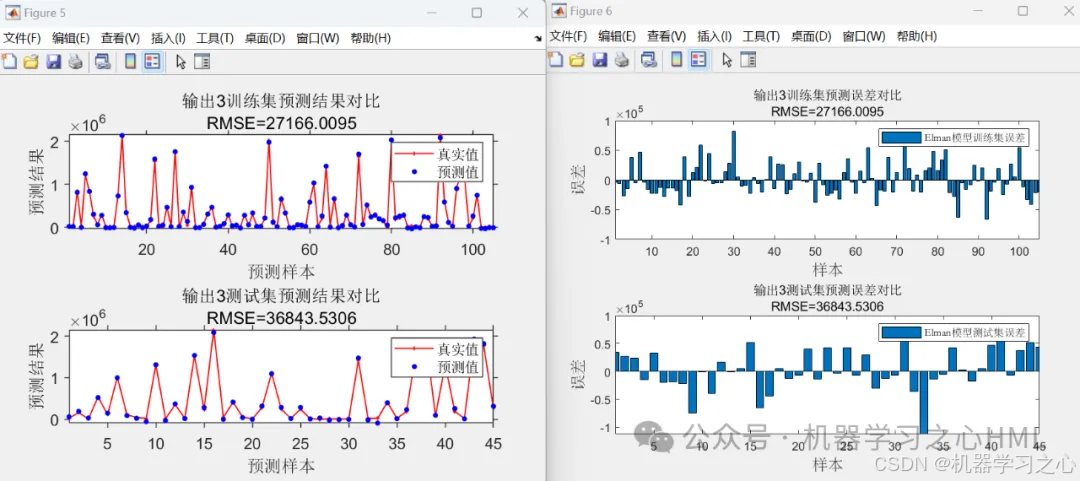
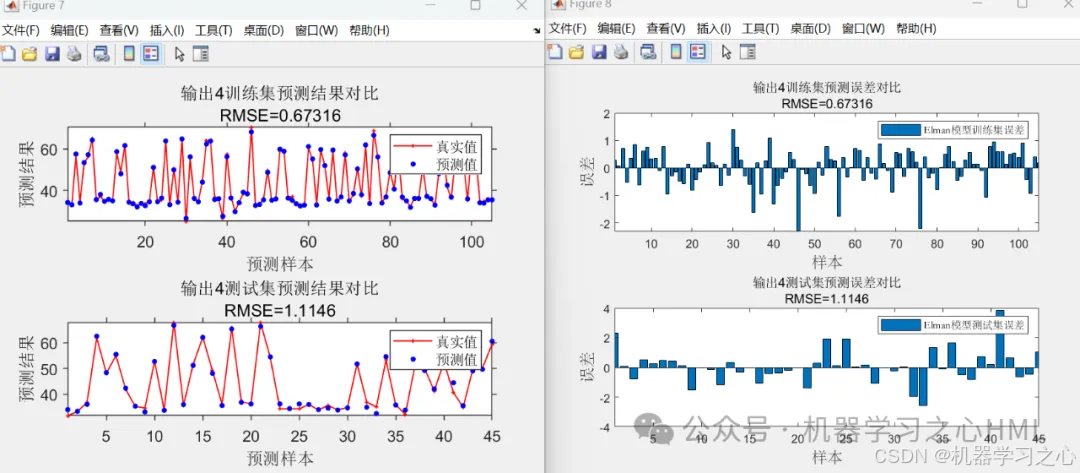
效果一览
基本介绍
1.Elman循环神经网络+NSGAII多目标优化算法,工艺参数优化、工程设计优化(Matlab完整源码和数据)
多目标优化是指在优化问题中同时考虑多个目标的优化过程。在多目标优化中,通常存在多个冲突的目标,即改善一个目标可能会导致另一个目标的恶化。因此,多目标优化的目标是找到一组解,这组解在多个目标下都是最优的,而不是仅仅优化单一目标。
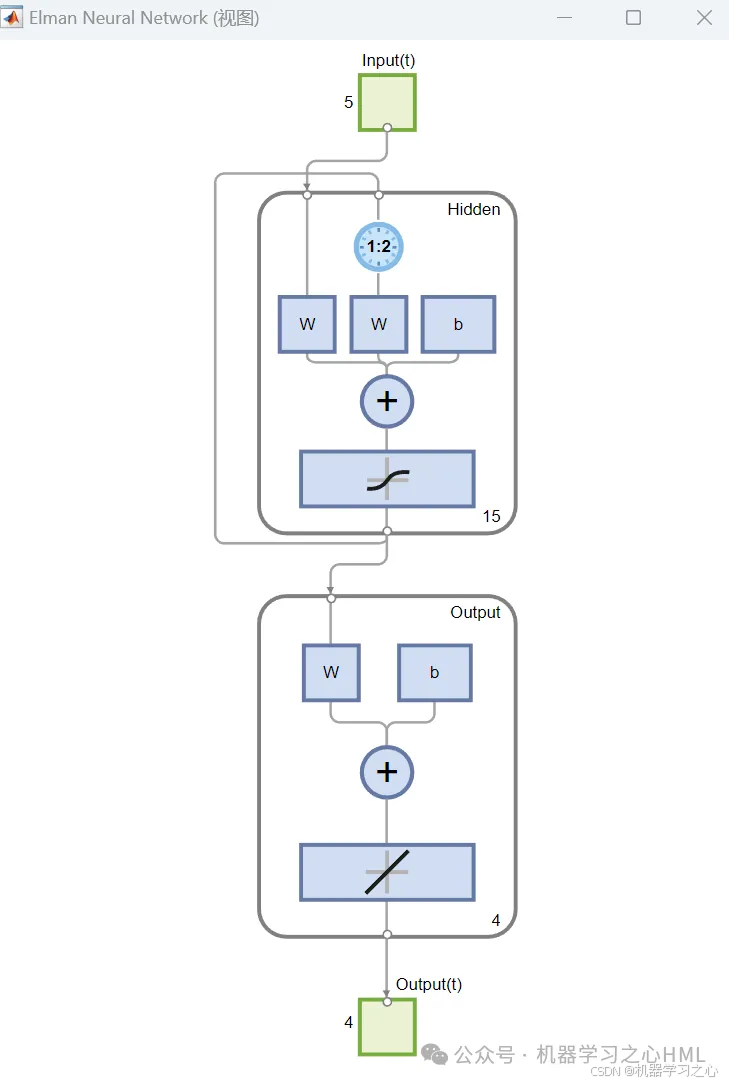
简单循环网络(simple recurrent networks,简称SRN)又称为Elman network,是由Jeff Elman在1990年提出来的。Elman在Jordan network(1986)的基础上进行了创新,并且简化了它的结构,最终提出了Elman network。
多目标优化是指在优化问题中同时考虑多个目标的优化过程。在多目标优化中,通常存在多个冲突的目标,即改善一个目标可能会导致另一个目标的恶化。因此,多目标优化的目标是找到一组解,这组解在多个目标下都是最优的,而不是仅仅优化单一目标。
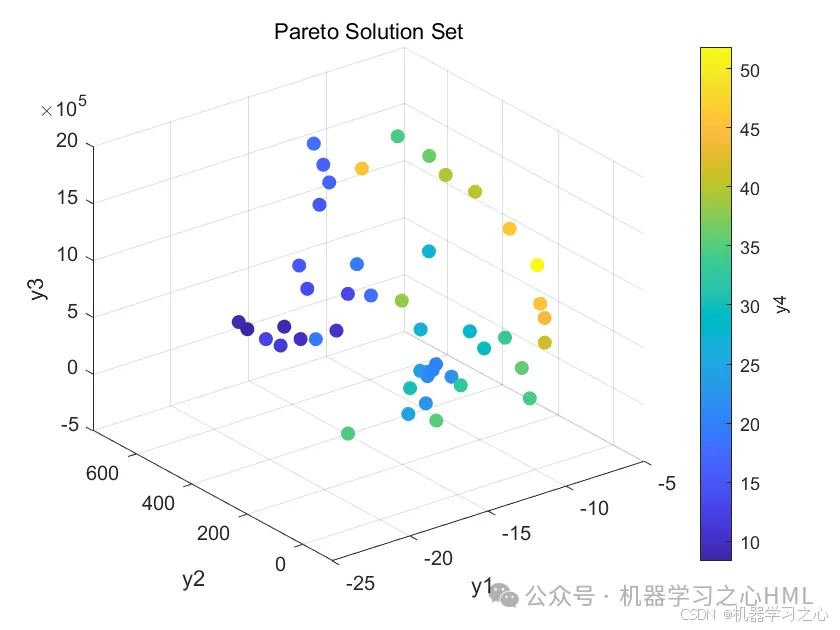
2.先通过Elman循环神经网络封装因变量(y1 y2 y3 y4)与自变量(x1 x2 x3 x4 x5)代理模型,再通过nsga2寻找y极值(y1极大;y2 y3 y4极小),并给出对应的x1 x2 x3 x4 x5Pareto解集。
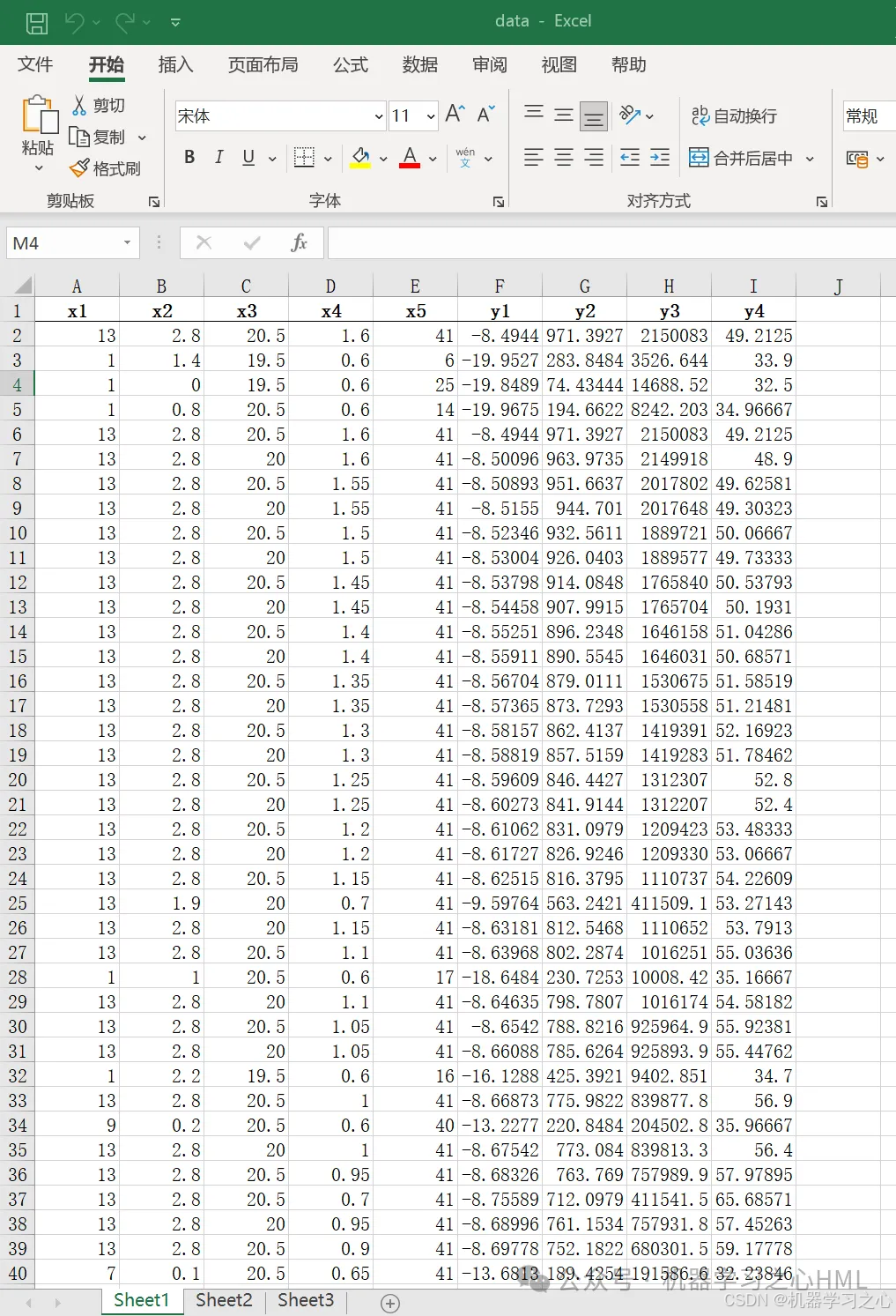
3.data为数据集,5个输入特征,4个输出变量,NSGAII算法寻极值,求出极值时(max y1; min y2;min y3;min y4)的自变量x1,x2,x3,x4,x5。
4.main1.m为Elman循环神经网络主程序文件、main2.m为NSGAII多目标优化算法主程序文件,依次运行即可,其余为函数文件,无需运行。
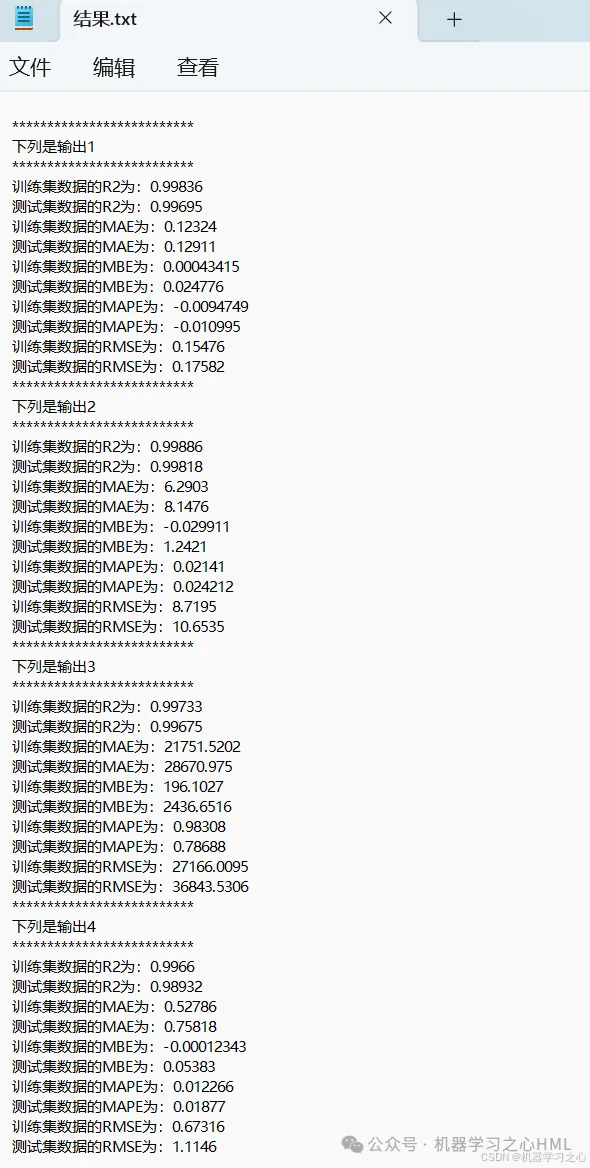
5.命令窗口输出R2、MAE、MBE、MAPE、RMSE等评价指标,输出预测对比图、误差分析图、多目标优化算法求解Pareto解集图,可在下载区获取数据和程序内容。
6.适合工艺参数优化、工程设计优化等最优特征组合领域。
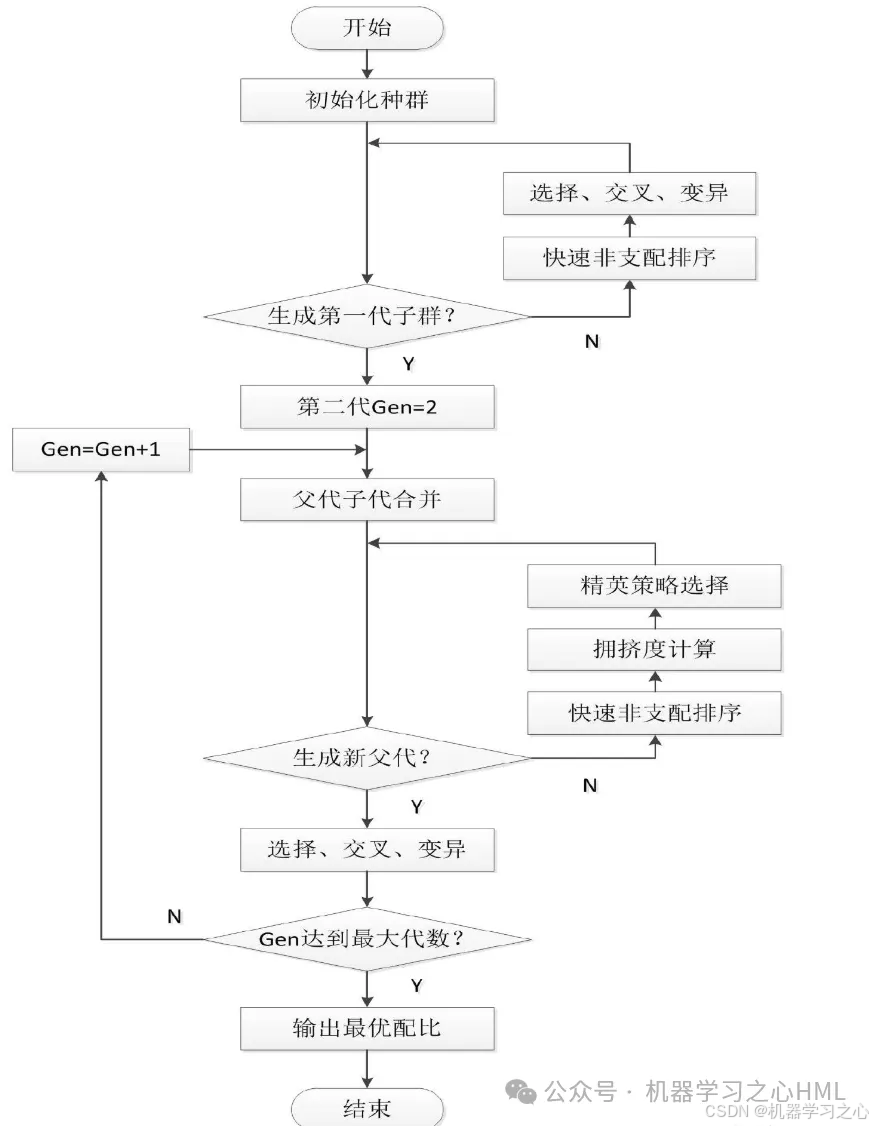
NSGA-II算法的基本思想与技术路线
1) 随机产生规模为N的初始种群Pt,经过非支配排序、 选择、 交叉和变异, 产生子代种群Qt, 并将两个种群联合在一起形成大小为2N的种群Rt;
2)进行快速非支配排序, 同时对每个非支配层中的个体进行拥挤度计算, 根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群Pt+1;
3) 通过遗传算法的基本操作产生新的子代种群Qt+1, 将Pt+1与Qt+1合并形成新的种群Rt, 重复以上操作, 直到满足程序结束的条件。
数据集
程序设计
- 完整程序和数据获取方式:私信博主回复工艺参数优化、工程设计优化上新!Elman循环神经网络+NSGAII多目标优化算法(Matlab)。
%% 仿真测试
t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test );
%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
%% 定义结果存放模板
empty.position = []; %输入变量存放
empty.cost = []; %目标函数存放
empty.rank = []; % 非支配排序等级
empty.domination = []; %支配个体集合
empty.dominated = 0; %支配个体数目
empty.crowdingdistance = [];%个体聚集距离
pop = repmat(empty, npop, 1);
%% 1、初始化种群
for i = 1 : npop
pop(i).position = create_x(var); %产生输入变量(个体)
pop(i).cost = costfunction(pop(i).position);%计算目标函数
end
%% 2、构造非支配集
[pop,F] = nondominatedsort(pop);
%% 计算聚集距离
pop = calcrowdingdistance(pop,F);
%% 主程序(选择、交叉、变异)
参考资料
工艺参数优化、工程设计优化!GRNN神经网络+NSGAII多目标优化算法(Matlab)
工艺参数优化、工程设计优化陪您跨年!RBF神经网络+NSGAII多目标优化算法(Matlab)
工艺参数优化、工程设计优化来袭!BP神经网络+NSGAII多目标优化算法(Matlab)