激活函数

激活函数（activation function）：将输入信号的总和转换为输出信号。

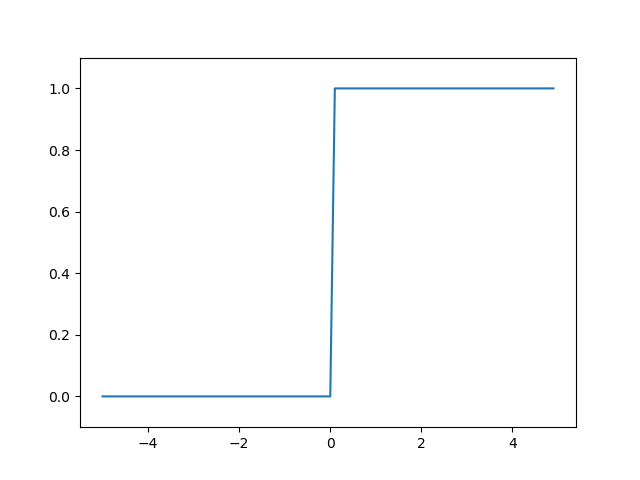
阶跃函数

python代码实现：

def step_function(x):
	y = x > 0
	return y.astype(np.int)  

对NumPy数组进行不等号运算后 ，数组的各个元素生成一个布尔型数组。
astype()方法转换NumPy数组的类型，数组y的元素类型从布尔型转换为int型。

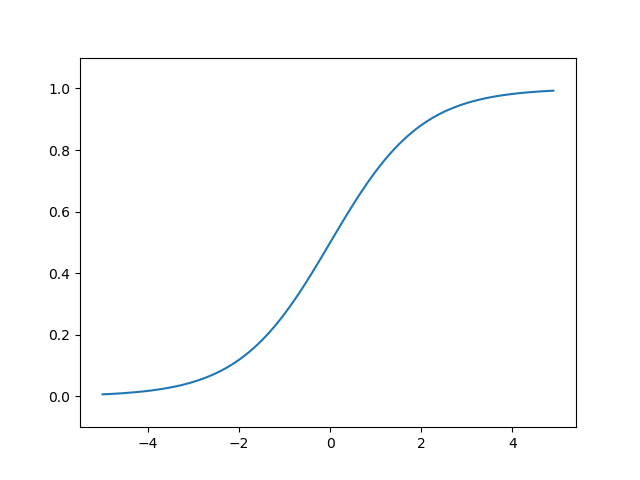
sigmoid 函数

sigmoid 函数数学公式：
$$h(x)=\frac{1}{1+e^{-x}}$$
python代码实现：

def sigmoid(x):
	return 1 / (1 + np.exp(-x))

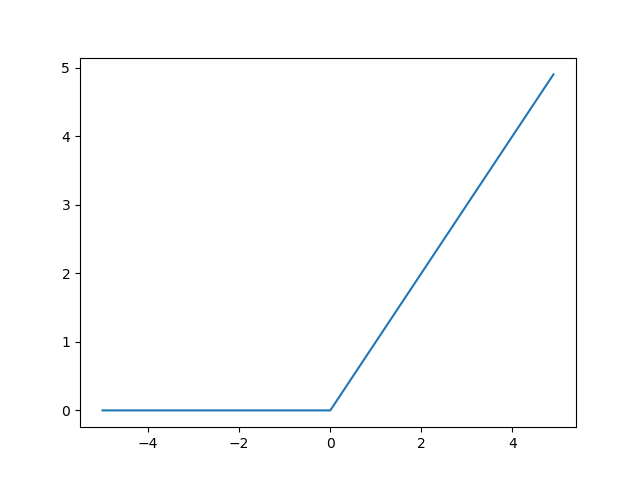
ReLU函数

ReLU：Rectified Linear Unit

ReLU 函数数学公式：
$$f(x)=\{\begin{array}{rlr}x& & (x>0)\\ y& & (x<0)\end{array}$$
python代码实现：

def relu(x):
    return np.maximum(0, x)

三层神经网络的实现

3层神经网络：
输入层（第0 层）有2 个神经元，
第1 个隐藏层（第1 层）有3 个神经元，
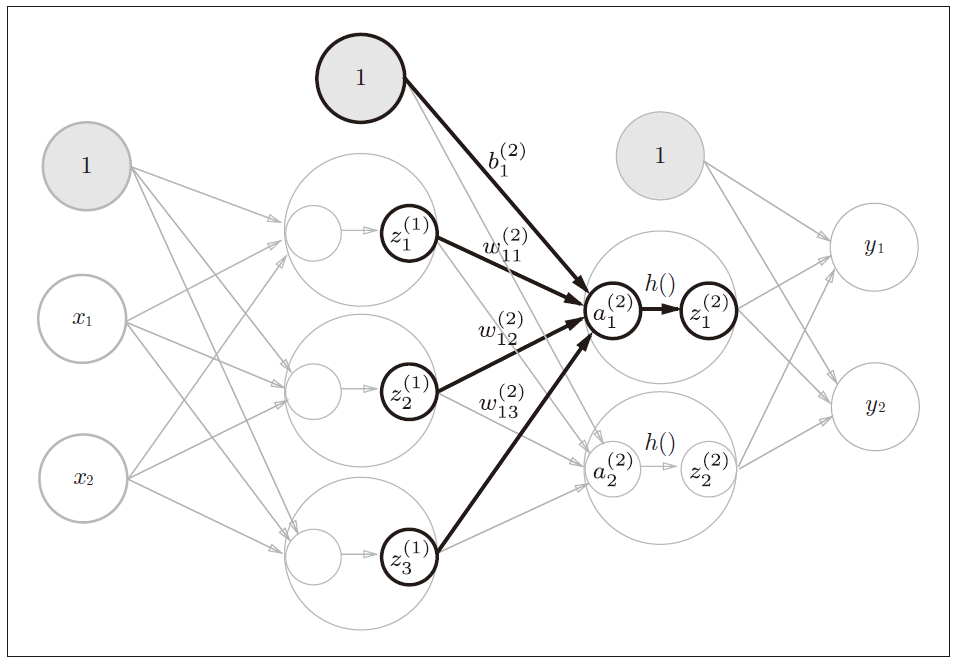
第2 个隐藏层（第2 层）有2 个神经元，
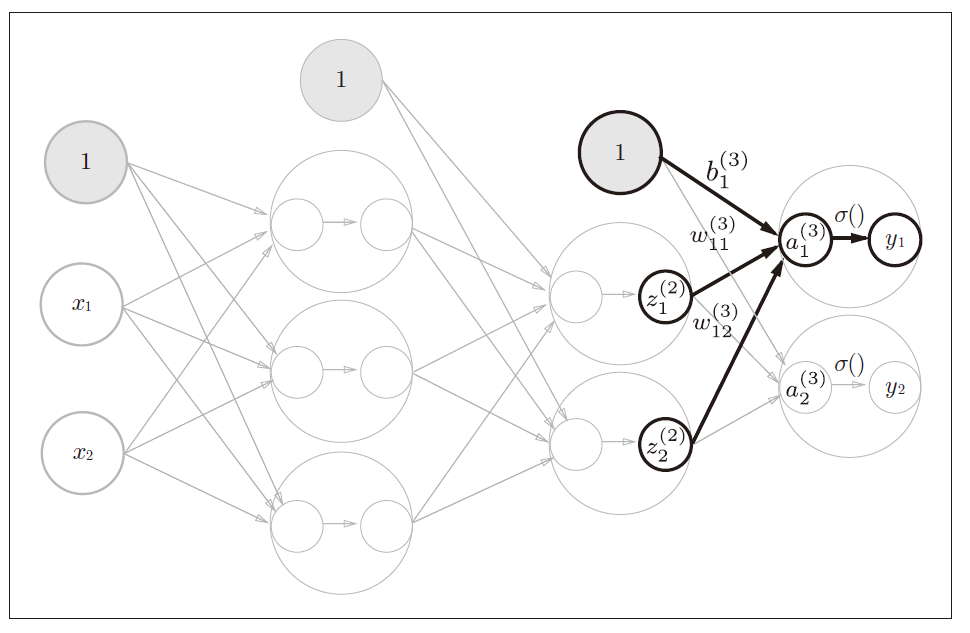
输出层（第3 层）有2 个神经元。

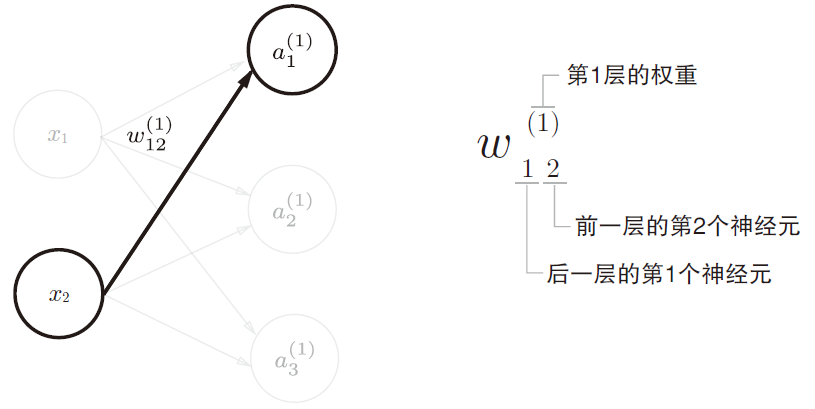
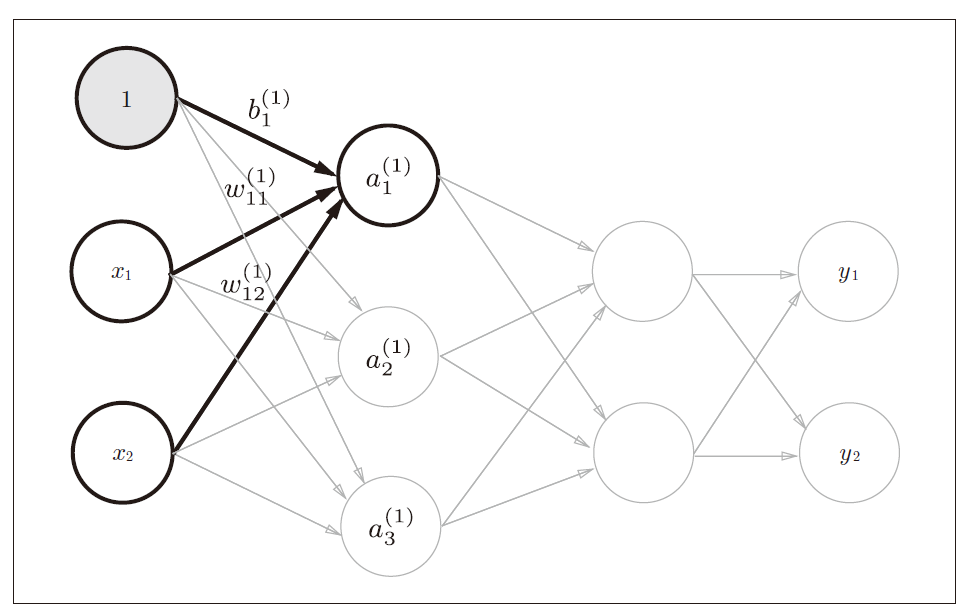
神经网络符号含义

各层间信号传递的实现

神经元“1”表示偏置，其右下角的索引号只有一个。这是因为前一层的偏置神经元（神经元“1”）只有一个。

用数学式表示$a{1}^{(1)}$，通过加权信号和偏置的和按如下方式进行计算
$$a{1}^{(1)}=w11^{(1)}x1+w12^{(1)}x2+b{1}^{(1)}$$ 使用矩阵的乘法运算，则可以将第1层的加权和表示成下面的式子
$$A^{(1)}=X{W}^{(1)}+B^{(1)}$$

其中$A^{(1)}$、$X$、$B^{(1)}$、$W^{(1)}$、如下所示。

$A^{(1)}=\left(\begin{array}{ccc}a{1}^{(1)}& a{2}^{(1)}& a{3}^{(1)}\end{array}\right)$，$X=\left(\begin{array}{cc}{x}_1& x_2\end{array}\right)$， $B^{(1)}=\left(\begin{array}{ccc}b{1}^{(1)}& b{2}^{(1)}& b{3}^{(1)}\end{array}\right)$,

$W^{(1)}=\left(\begin{array}{ccc}{w}_{11}^{(1)}& w_{21}^{(1)}& w_{31}^{(1)}\\ w_{11}^{(1)}& w_{21}^{(1)}& w_{31}^{(1)}\end{array}\right)$

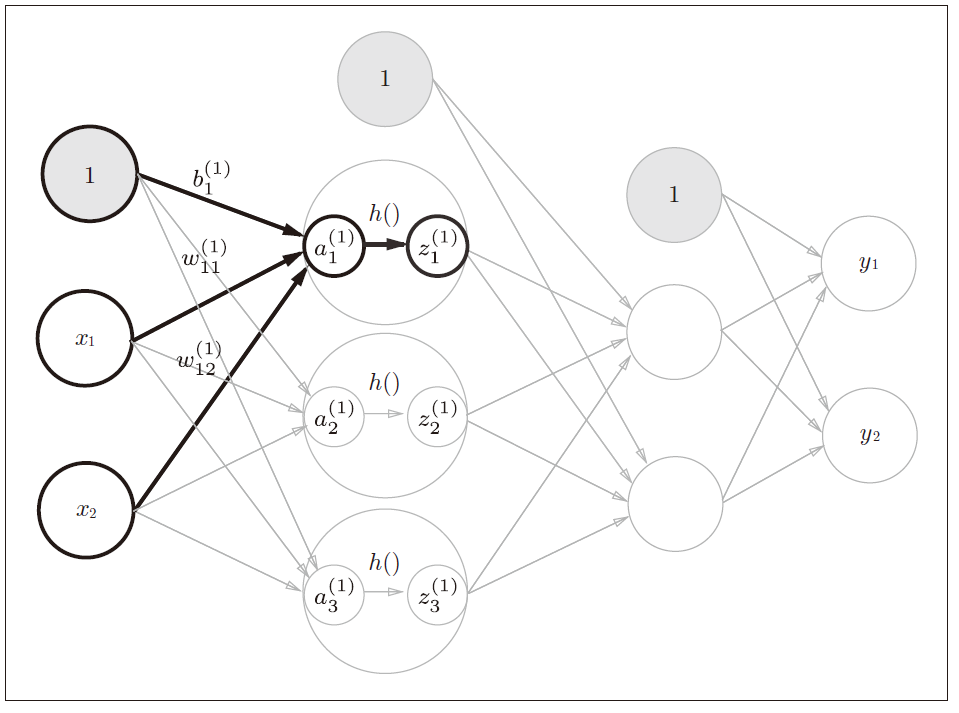
$a$表示隐藏层的加权和（加权信号和偏置的总和）
$z$表示激活函数转换后的信号
$h()$ 表示激活函数，这里使用sigmoid 函数

这里使用identity_function()恒等函数作为输出层的激活函数，记为$\sigma ()$。

三层网络python代码实现

import numpy as np

def sigmoid(x):
	return 1 / (1 + np.exp(-x))

def identity_function(x):
	return x

def init_network():
	network = {}
	network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
	network['b1'] = np.array([0.1, 0.2, 0.3])
	network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
	network['b2'] = np.array([0.1, 0.2])
	network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
	network['b3'] = np.array([0.1, 0.2])

	return network

def forward(network, x):
	W1, W2, W3 = network['W1'], network['W2'], network['W3']
	b1, b2, b3 = network['b1'], network['b2'], network['b3']

	a1 = np.dot(x, W1) + b1
	z1 = sigmoid(a1)
	a2 = np.dot(z1, W2) + b2
	z2 = sigmoid(a2)
	a3 = np.dot(z2, W3) + b3
	y = identity_function(a3) # 或者Y = A3

	return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [ 0.31682708 0.69627909]

softmax函数

公式如下：
$$y_k=\frac{e^{a_k}}{{\sum }_{i=1}^n{e}^{a_i}}$$
softmax 函数的分子是输入信号$a_k$的指数函数，分母是所有输入信号的指数函数的和。

机器学习的问题大致可以分为分类问题和回归问题。回归问题用恒等函数，分类问题用softmax 函数

手写数字识别

MNIST数据集是由0到9的数字图像构成的。训练图像有6万张，测试图像有1万张。

神经网络的输入层有784个神经元，输出层有10个神经元。
输入层的784这个数字来源于图像大小的28 × 28 = 784，输出层的10这个数字来源于10类别分类（数字0到9，共10类别）。
这个神经网络有2个隐藏层，第1个隐藏层有50个神经元，第2个隐藏层有100个神经元。这个50和100可以设置为任何值。

import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax


def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test


def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
    return network


def predict(network, x):
    w1, w2, w3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, w1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, w2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, w3) + b3
    y = softmax(a3)

    return y


x, t = get_data()
network = init_network()

batch_size = 100 # 批数量
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x))) # Accuracy:0.9352

p = np.argmax(y)
获取概率最高的元素的索引。矩阵的第0维是列方向，第1维是行方向。

>>> x = np.array([[0.1, 0.8, 0.1], [0.3, 0.1, 0.6],
... [0.2, 0.5, 0.3], [0.8, 0.1, 0.1]])
>>> y = np.argmax(x, axis=1)
>>> print(y)
[1 2 1 0]

np.sum(p == t[i:i+batch_size])

NumPy数组之间使用比较运算符（==）生成由True/False构成的布尔型数组，并计算True的个数

>>> y = np.array([1, 2, 1, 0])
>>> t = np.array([1, 2, 0, 0])
>>> print(y==t)
[True True False True]
>>> np.sum(y==t)
3

对神经网络的输入数据进行某种既定的转换称为预处理（pre-processing）。
作为对输入图像的一种预处理，我们进行了正规化（normalization）。
将数据整体的分布形状均匀化的方法，即数据白化（whitening）。
输入数据的集合称为批。通过以批为单位进行推理处理，能够实现高速的运算。