多目标跟踪(MOT)中的卡尔曼滤波(Kalman filter)和匈牙利(Hungarian)算法详解
1. 概览
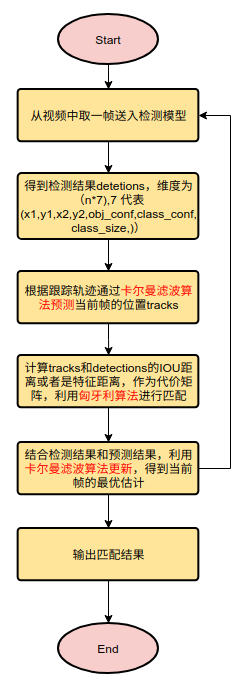
在开始具体讨论卡尔曼滤波和匈牙利算法之前,首先我们来看一下基于检测的目标跟踪算法的大致流程。
2. 卡尔曼滤波(Kalman filter)
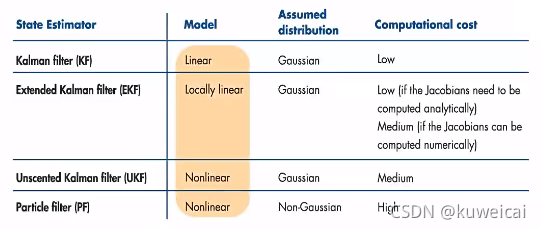
目标跟踪中使用的就是最基础的 Kalman filter 算法。这里也仅仅讨论最基础的 Kalman filter 算法。
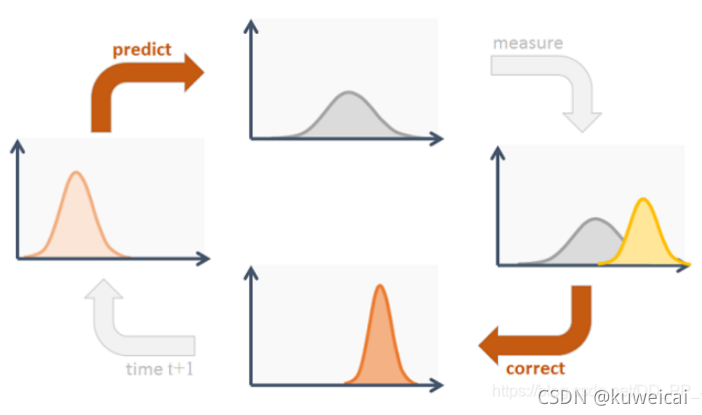
卡尔曼滤波算法的过程很简单,如下图所示。最核心的两个步骤就是预测和更新(下图的 correct)。
在目标跟踪任务中,目标的状态变量表示为 x , y , a , h , v x , v y , v a , v h x, y, a, h, vx, vy, va, vh x,y,a,h,vx,vy,va,vh,其中 x , y x, y x,y 表示目标框的中心坐标, a a a 表示目标框的高宽比, h h h 表示目标框的高,在卡尔曼滤波算法中也表示为 mean; v x , v y , v a , v h vx, vy, va, vh vx,vy,va,vh 分别表示对应变量的速度,也称之为 covariance。在 DeepSORT 和 ByteTrack 算法中都是使用的具有等速运动和线性观测模型的标准卡尔曼滤波器。
2.1 预测
预测就是根据目标在 t-1 时刻的状态来预测其在 t 时刻的状态。预测主要分为两部分。
{ x ′ = F x ( 1 ) P ′ = F P F T + Q ( 2 ) \left\{\begin{aligned} & x' = Fx &(1)\\ & P' = FPF^T + Q &(2) \end{aligned}\right. {
x′=FxP′=FPFT+Q(1)(2)
在公式 1 中,x 为 track 在 t-1 时刻的均值,F 称为 状态转移矩阵,该公式预测 t 时刻的 x’。
在公式 2 中,P 为 track 在 t-1 时刻的协方差,Q 为系统的噪声矩阵,代表整个系统的可靠程度,一般初始化为很小的值,该公式预测 t 时刻的 P’。
对于的代码如下。
def predict(self, mean, covariance):
"""Run Kalman filter prediction step.
Para